考虑气温变化影响的引水渠道水内冰演变数值模拟

王晓玲，周正印，蒋志勇，周莎莎，张自强

(1. 天津大学建筑工程学院，天津 300072；2. 天津大学环境科学与工程学院，天津 300072；3. 中水北方勘测设计研究有限责任公司，天津 300222)

我国新疆地处高寒地区，冬季气温低，流冰期长，冰流量大，水流量小，容易形成冰害，因而大多数引水式水电站采用输排冰运行方式．当气温使水温降到0,℃以下时，水电站引水渠道内开始形成冰花，进入结冰期．随着气温的进一步下降，渠道中产冰量迅速增大，容易形成冰塞、冰坝等冰害，这些冰害对水电站的正常运行、安全输水以及周围的生态环境产生很大影响，因此气温是影响渠道中产冰量的重要影响因素．本文以新疆某水电站为例，分析了不同气温下引水渠道中水内冰的演变规律，这对于保证当地的工农业生产、人民的正常生活及水电站的运行管理等方面具有重大意义．因此，研究寒冷地区冬季渠道冰害演变规律有利于水利工程的安全和水资源的可持续利用．

根据新疆某水电站多年统计资料表明，该水电站引水渠道中冰的主要存在形式为水内冰，因此本研究主要对引水渠道中水内冰的演变进行数值模拟研究，探讨气温变化条件下引水渠道中水内冰的沿程分布规律．

国外对水内冰的研究起步较早，Simonsen等、Petryk、Michel和 Drouin、Calkins等分别采用恒定流理论对河流的冰冻过程进行了数值模拟，但这些模型建立在恒定或准恒定状态水力模型基础上，均没有考虑冰花浓度与水温分布的沿程变化[1]；Lal等[2]、Wang等[3]、Shen等[4]建立了综合河冰模型 RICE，水力因素采用一维非恒定流方程确定，热力因素由热量方程确定，水流的温度变化和冰花流量由热能方程确定，但未考虑太阳辐射、有效辐射和蒸发热损失等．茅泽育等[5-6]采用一维和平面二维河冰数学模型进行了数值模拟，热量模型中考虑了水内冰释放潜热与水表热损失分别对天然河道冰塞演变发展过程以及水内冰演变过程的影响，取得了较好的结果．王晓玲等[7]建立了三维欧拉两相流模型，数学模型中考虑了热量交换，模拟了不同引水流量下水电站引水渠道中水内冰演变．

综上所述，目前水内冰的研究模型中大多考虑了水面对流热损失，但是较少考虑太阳辐射、有效辐射和蒸发热损失的影响，且模型多限于一、二维模拟，将实际的三维问题进行了简化，认为各参量在宽度方向均匀分布，与实际情况不符．因此，笔者基于计算机流体动力学(computational fluid dynamics，CFD)技术，建立完善、适用的具有动态性的三维引水渠道水内冰演变数学模型，研究气温变化条件下引水渠道中水内冰的演变规律，并讨论了太阳辐射、有效辐射和蒸发热损失对水内冰分布的影响．

1 数学模型

采用非稳态Euler-Euler 两相流k-ε 紊流模型，水相为液相，冰相为颗粒相，视冰相为连续介质．颗粒相可以看作一种拟流体，认为颗粒与流体是共同存在且相互渗透的连续介质．

1.1 控制方程

1)连续性方程

式中：t为时间，s；kα为第k相的体积分数；kρ为第k相的密度，kg/m3；ku 为第 k相的平均速度矢量，m/s；下标 i l,k=、 i为冰相，l为水相，水相密度lρ为997.561,kg/m3，冰相密度iρ为900,kg/m3．

2)动量方程

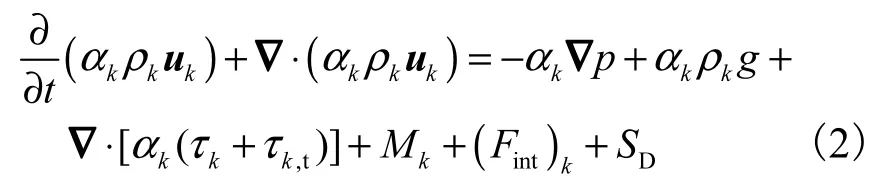
式中： p为流体微元体上的压力，Pa；g为重力加速度，9.8,m/s2；kτ、,tkτ分别为层流和湍流应力，N/m2；为单位体积相间动量传递，即包括曳力DF、升力LF和虚拟质量力为内在力，N/m3；DS 为动量源项为进口分散相浓度，mol/L；sM 为固相的相对分子质量，kg/m3．

3)水相湍动能k方程

4)水相耗散率ε方程

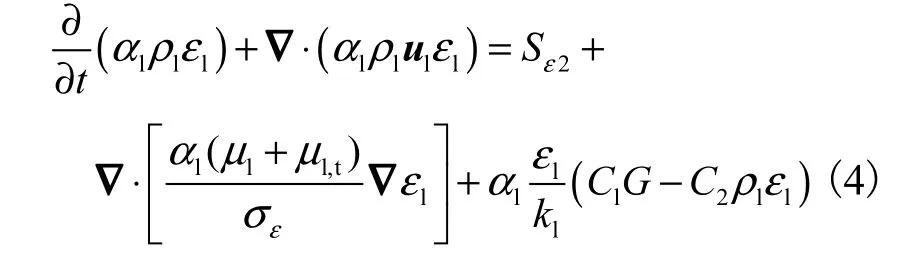
式中：lk为水相湍动能，m2/s2；lu为水相流速，m/s；lμ为水相分子黏性，N·s/m2；l,tμ为水相湍流分子黏性，N·s/m2；kσ、εσ分别为k、ε方程的湍流Prandtl数；为湍动能lk的扩散率，N/s；C1、C2为高雷诺数 -kε方程的无因次常数；2Sε、表示两相间的相互作用，其中 Ct为响应函数； σk、σε、C1、C2分别为 0.9、1.22、1.44 和 1.92[8]．

5)温度方程

式中：uj为纵向流速在 j方向上的分量，m/s；lT为水温，K；eν为有效黏度，m/s2；Tσ为紊流模型系数；Sb、Sf为源项[7]，d为水内冰颗粒的直径，0.01,m；cp为水的比热，4,181.72,J/(kg·K)；nq 为单位面积上的热交换量，J/m2；为太阳辐射(为太阳直接辐射和太阳散射辐射之和)；anJ 为反辐射热损失；wrJ 为有效辐射；ccJ 为水面对流热损失；ecJ为蒸发热损失，kJ/m2.

1.2 初始条件

在水电站引水渠道中，假设渠道进口处冰花均匀分散在水中．根据实测资料，冰晶籽成籽率取 10-6,kg/(m2·s)，进口处冰花温度设定为气温，水流温度设定为 0,℃，将气温分别设定为－5,℃、－10,℃、－15,℃、－20,℃和－25,℃，渠道的边坡比为 1∶2，其余参数见表1.

表1 计算参数Tab.1 Calculation parameters

1.3 边界条件

(1)入口边界：假设渠道入口流速、冰体积分数、湍动能等为均匀分布，in/u Q A= ，Q为引水流量，80,m3/s；A为引水渠道截面积，m2；紊流动能紊流动能率考虑单一冰花粒径，取1,cm.

(2)出口边界：计算域的出口边界上，各速度分量uvw、、以及k和ε均取第2类齐次边界条件.

(3)压力边界：压力边界设为恒压边界，表示渠道中水面与外界大气相通.温度设定为气温，压力为标准大气压.

(4)固体壁面：电站引渠边壁均为无滑动壁面边界，流体计算域边界采用考虑粗糙度影响的壁面函数[9].

1.4 求解方法

把质量方程、动量方程、组分方程和湍流模型方程等微分方程写成通用形式[10]，即

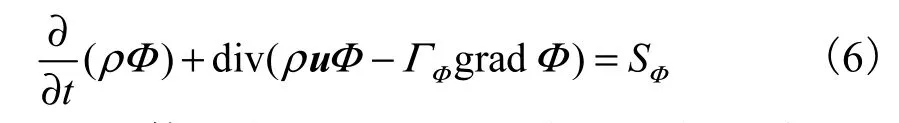
式中：u为流体速度矢量，m/s；Φ表示因变量(如 ui、ul、k、ε等)；ΓΦ为对应于Φ的扩散系数，m2/s；SΦ为对应于Φ的源项，N/m3．式(6)由 4项组成，它们依次为瞬变项(或时间导数项)、对流项、扩散项和源项．对通用形式控制方程采用有限体积法进行求解，对流项采用二阶迎风差分格式离散方程、SIMPLE算法求解．

2 模型验证

采用吴剑疆等[5]对黄河上游河道中水内冰演变的研究结果作为验证．河段长度 L＝4,km，水深 h＝5,m，边坡系数为 20，进口流量为 500,m3/s，冰花粒径考虑为单一粒径，取文献[5]中各不同粒径的平均值，2.5,mm，冰晶籽成籽率取 10-5,kg/(m2·s)，水面失热率为500,W/m2．计算模型共划分为50,000个网格，其中网格长度为 x ×y×z=4 m× 1m× 4 m ，如图1所示．图2为对比结果．

图1 河道模型网格划分Fig.1 Computational mesh of river channel

图2 本文模拟值与吴剑疆计算值对比Fig.2 Comparison between numerical simulation and results reported by Wu Jianjiang

由图 2(a)可知，水温沿程分布呈现先降低后升高的分布趋势，水温沿程出现最低点．与验证值进行比较，模拟结果与验证结果基本相符，两者之间最大误差为 12.1%，平均误差为 7.58%．由图 2(b)可知，由于水表沿程失热，水流在流动过程中不断产冰，水内冰体积分数沿程逐渐增大．通过与验证结果对比，可见模拟结果与验证结果基本相符，模拟结果与验证结果之间最大误差为 10.45%，平均误差为 5.29%．说明模型能较好地反映渠道中水内冰的演变过程.

图3为河道出口断面冰体积分数分布．由图可知，出口断面表层平均冰体积分数为 0.025,39，文献[5]中出口断面表层平均冰体积分数为 0.023,57，二者之间误差为7.17%，模拟结果与已有结果比较符合．

图3 河道出口断面冰体积分数分布Fig.3 Distribution of ice volume fraction on outlet section of river channel

3 模型应用

新疆某水电站引水渠道全长 64.5,km，分别研究了引水流量为 80,m3/s，风速为 21,m/s，气温为－5,℃以及－10,℃、－15,℃、－20,℃、－25,℃ 5 种工况下引水渠道中水内冰的演变，获得了沿程产冰量随引水流量的变化趋势．各工况参数见表2．

表2 不同工况下参数表Tab.2 Parameters under various conditions

3.1 网格划分

由于电站引渠长宽高比例大，因此在全局显示的情况下将使得引渠在 y、z方向网格几乎无法清楚显示.模型以引水渠道取水口进口至渠道排冰闸前一段渠道为原型，图 4(a)给出了模型的全局，可以看出渠道断面几乎为线状，但渠道各弯道及转弯仍可见．图4(b)为模型进口一段模型．渠道断面为梯形断面，模型共划分为16×104个网格．

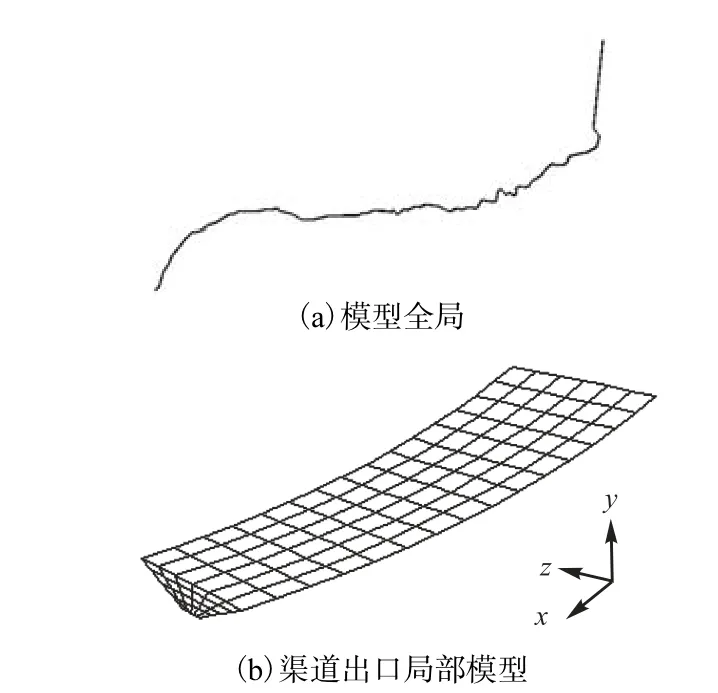
图4 引水渠道计算网格模型Fig.4 Computational mesh for diversion channel

3.2 网格灵敏性分析

网格密度对数值模拟计算精度有较大影响．一般来说，相同边界条件下，网格密度越大，模拟所得结果越接近实际值；但计算机资源的耗用也随网格密度的增加而大大提高，因此网格的划分需要兼顾准确性和计算效率．为分析不同网格密度的计算精度，本文同时对引水渠道模型细网格、较细网格、粗网格进行了对比模拟计算．表3列出了3种网格密度下的网格及计算时间的比较，图 5为不同密度网格的比较，图 6为模拟结果的对比．

对比图6与表3可知，粗网格计算结果与其他两种网格差别较大，冰花在渠道中分布分散，与理论分析结果不符；而细网格与较细网格的计算结果接近，冰花主要集中在渠道表层，与理论分析结果相符；但细网格耗用计算时间较长，为 151,h，约为较细网格计算时间的 2倍，计算效率低．综合考虑计算效率和结果的准确性，此次计算采用较细网格模型进行计算．

表3 3种网格密度比较Tab.3 Comparison of three mesh densities

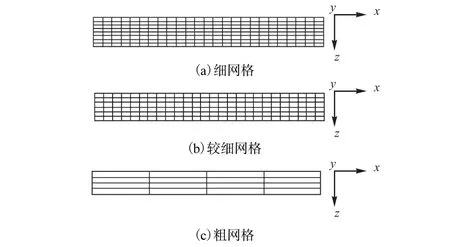
图5 不同密度的网格比较Fig.5 Comparison of meshes with various densities

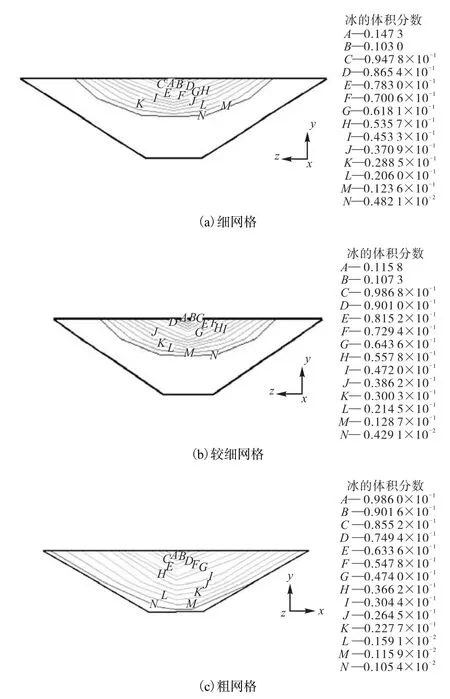
图6 不同网格密度下模拟结果对比Fig.6 Comparison of simulated results between meshes with various densities

3.3 不同气温下的计算结果分析

在引水流量为 80,m3/s、风速为 21,m/s的条件下，通过对比气温为－5,℃ 以及－10,℃、－15,℃、－20,℃、－25,℃下的工况 1、工况 5中水内冰演变及分布规律，以分析气温对引水渠道中产冰量的影响．由于不同工况下流速、温度、冰体积分数及产冰量的分布规律相同，故仅对工况1下气温及产冰量的沿程分布进行详细分析，其他工况不再赘述．

3.3.1 工况1下流速分布规律

流速是水内冰生成、演变、输移的主要动力因素．当渠道流速大于临界输冰流速时，由于水流的紊动和拖曳作用，水面上的冰花不会相互粘结形成冰盖．

图7为渠道不同渠段水流流速分布．图 7(a)为渠道进口渠段水流流速分布，由图可知，在渠道进口渠段中，渠道中心水流流速明显增加，而在渠道两侧，由于水流受到边壁的摩擦阻力，水流流速变化不明显；图7(b)为渠道出口渠段水流流速分布，由图可知，在出口渠段中由于渠道转弯而使得渠道主流线由凹岸偏向凸岸，凸岸一侧水流流速呈现先增大后减小、而凹岸一侧水流流速呈现先减小后增大的分布规律．

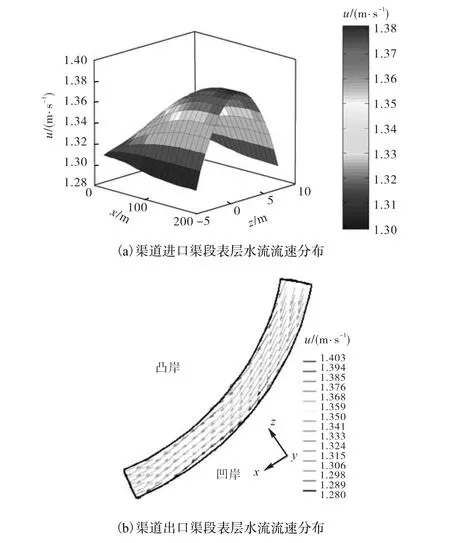
图7 引水渠道不同渠段水流流速分布Fig.7 Distribution of water velocity in various channel sections

3.3.2 工况1的冰体积分数沿程分布

图8分别为不同断面y-z剖面处的体积分数等值线，x为渠道长度．由图 8可知，在渠道起始段中，冰体积分数很小，由于冰水的掺混作用，冰在水中的分布比较分散；随着水流流动，新冰不断生成，渠道断面上冰的体积分数逐渐增大．渠道表层水域中的冰体积分数的增加主要是因为在水流流动过程中逐渐产冰，且新产冰受到浮力影响上浮至表层水域的原因；在各个断面处，冰体积分数沿水深均呈逐渐降低趋势，渠道中心处冰体积分数高于两侧．

3.3.3 工况1的温度分布规律

如图 9(a)所示，在 0～150,m 左右，渠道中冰的温度迅速增大，之后变化趋于平缓.如图 9(b)所示，在靠近进口边界的渠道中，由于水内冰浓度较小，水内冰和水体之间的热交换量较小，结冰潜热不足以补偿水表面的热损失，水温沿程持续下降，在 35,km 左右出现最低点，之后水温逐渐上升；随着水内冰浓度的增大，结冰潜热补偿增大，水温逐渐上升．

图8 渠道典型断面处冰体积分数分布Fig.8 Distribution of ice volume fraction on typical sections of channel

3.3.4 不同工况下冰体积分数沿程分布

对比图10中不同气温下表层水域中冰体积分数的变化，可知各种不同工况下，冰的体积分数在30,km 以前均维持在很低的水平，可认为此段渠道中基本不产冰，产冰突变点之后，冰体积分数迅速增大；随着气温由-5,℃降至－25,℃，最终的产冰量和冰体积分数逐渐增大，产冰出现的位置逐渐向上游移动．

3.3.5 产冰量模拟结果验证

渠道产冰量计算经验公式为[11]

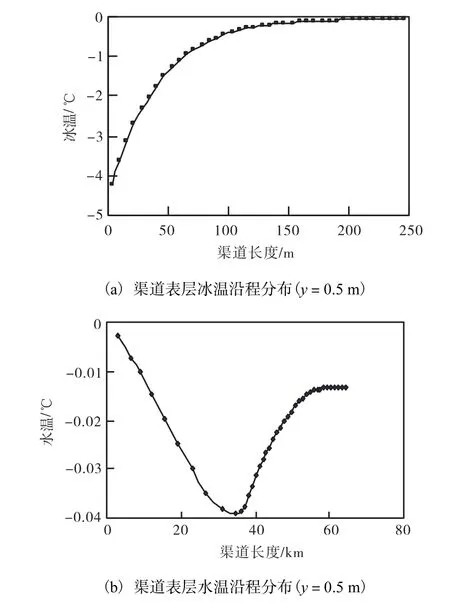
图9 渠道表层冰温与水温沿程分布Fig.9 Distribution of ice temperature and water temperature on the surface layer along channel

图10 不同气温下表层水域中冰体积分数沿程分布Fig.10 Distribution of ice volume fraction on surface layer along channel at various air tempera ture

式中：l为渠道长度；B为渠道宽度；iγ为冰的密度；β为修正系数；1S为太阳直接辐射热；S2为太阳散射辐射热；S3为反射辐射热损失；S4为有效辐射；S5为蒸发热损失；S6为水面对流热损失；S7为渠道沿线水混入热损失；S8为河床与水流之间的热量交换；S9为水流动力加入热量；S10为降水进入渠道的热量交换；110～SS的单位均为2MJ/(m d)⋅.

图11为不同工况下模拟与经验产冰量对比.将模拟得到的产冰量与《凌汛计算规范》中经验计算产冰量对比，可知经验值与模拟值之间最大误差为8.54%，平均误差为4.43%．通过与经验公式计算得到的产冰量对比，验证了数值模拟的可靠性．通过对比可知，模拟所得产冰量与经验公式计算产冰量相符．

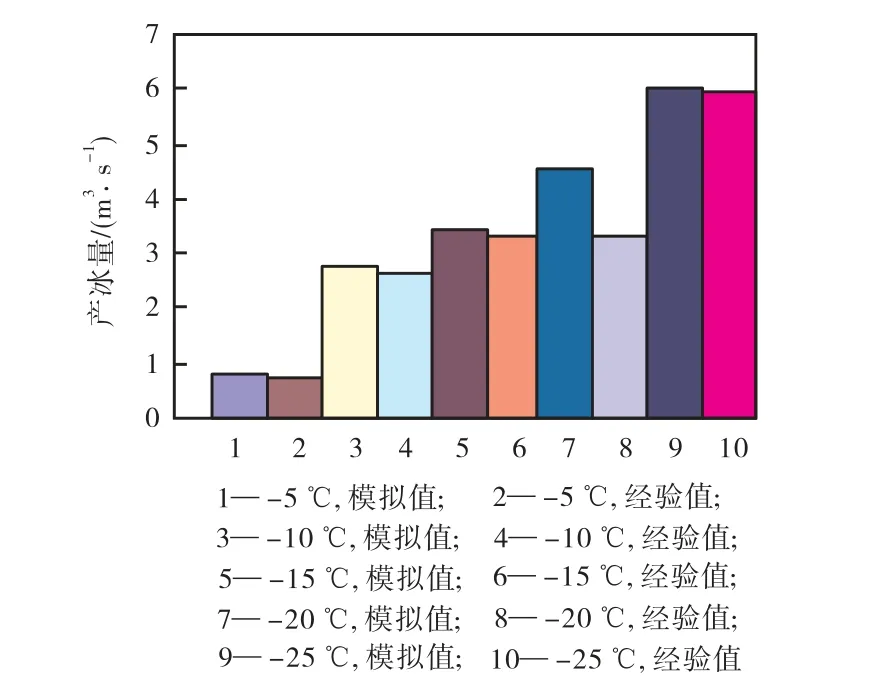
图11 不同工况下模拟与经验产冰量对比Fig.11 Comparison of simulated and empirical quantities of ice

3.3.6 太阳辐射、有效辐射和蒸发热损失对水内冰分布的影响

热量是水内冰生成、演变的主要影响因素，模型之间的热量传递直接影响渠道中产冰量的大小，影响渠道中水内冰演变及分布．鉴于目前模型当中较少考虑太阳辐射、有效辐射、蒸发热损失对水内冰演变的影响.本文以工况 5(见图 12)为例，对模型中太阳辐射、有效辐射、蒸发热损失对水内冰分布的影响进行了讨论．

图12(a)为考虑太阳辐射、有效辐射、蒸发热损失情况下，工况 5出口断面冰体积分数分布，经计算渠道产冰量为 6.02,m3/s；图 12(b)为未考虑太阳辐射、有效辐射、蒸发热损失情况下，工况 5渠道出口断面冰体积分数分布，经计算渠道产冰量为 5.03,m3/s．将两种情况下渠道产冰量与经验产冰量对比，两者误差分别为 1.17%和 18.3%，可见，未考虑太阳辐射、有效辐射、蒸发热损失的模型模拟得到的产冰量与经验计算产冰量偏差较大．

图12 渠道出口断面处冰体积分数分布对比Fig.12 Comparison of ice volume fraction distribution on outlet section of channel

4 结 论

(1)建立了三维非稳态Euler-Euler 两相流 -kε紊流模型，动量方程考虑了相间曳力、升力和虚拟质量力，热量传递方程中考虑了冰水之间的热量传递以及太阳辐射、有效辐射、蒸发热损失、水面对流热损失等热量传递，通过与吴剑疆等黄河上游河道中水内冰演变结果对比及经验产冰量的对比，验证了模型的可靠性．

(2)采用贴体网格建立了三维引水渠道的网格模型，对网格划分的灵敏性进行了分析，得到了一种兼顾网格密度与计算效率的网格划分．

(3)模拟分析了水电站引水渠道中气温变化条件下冰温、水温及冰体积分数的沿程分布规律；讨论了太阳辐射、有效辐射和蒸发热损失对水内冰分布的影响．结果表明：水温沿程先降低后增加，沿程出现最小值，冰温沿程迅速增加；冰的体积分数沿程存在突变点，且突变点在水温最低点附近．随着气温逐渐降低，最终冰体积分数和产冰量逐渐增大，冰体积分数沿程突变点逐渐向渠道上游移动；考虑太阳辐射、有效辐射和蒸发热损失影响的模型的模拟结果与经验计算产冰量偏差较小．

通过对水电站引水渠道中气温变化对水内冰演变的模拟，以期为寒冷地区冬季引水渠道的施工及安全运行和水资源的可持续利用提供理论依据．

［1］ 茅泽育，董曾南，陈长植. 河冰数学模拟研究综述[J].水力发电学报，1996 (12)：58-61.Mao Zeyu，Dong Zengnan，Chen Changzhi. The summary of river ice numerical simulation[J]. Journal of Hydroelectric Engineering，1996 (12)：58-61(in Chi-nese)．

［2］ Lal A M，Shen H T. Mathematica-model for rivel ice processes[J]. Hydraul Eng-ASCE，1991，117：851-867.

［3］ Wang D S，Shen H T，Randy D. Simulation and analysis of Upper Niagara River ice-jam conditions[J]. Journal of Cold Regions Engineering，1995，9(3)：119-134.

［4］ Shen H T，Wang D S. Under cover transport and accumulation of frazil granules[J]. Journal of Hydraulic Engineering，1995，121(2)：184-195.

［5］ 吴剑疆，茅泽育，王爱民，等. 河道水内冰演变的数值计算[J]. 清华大学学报， 2003，43(5)：702-705.Wu Jianjiang，Mao Zeyu，Wang Aimin，et al. Numerical simulation of frazil ice evolution in rivers[J]. Journal of Tsinghua University，2003，43(5)：702-705 (in Chinese)．

［6］ 茅泽育，吴剑疆，张 磊，等. 天然河道冰塞演变发展的数值模拟[J]. 水科学进展，2003，14(6)：700-705.Mao Zeyu，Wu Jianjiang，Zhang Lei，et al. Numerical simulation of river ice jam[J]. Advances in Water Science，2003，14(6)：700-705 (in Chinese)．

［7］ 王晓玲，张自强，李 涛，等. 引水流量对引水渠道水内冰演变影响的数值模拟[J]. 水利学报，2009，40(11)：10-15.Wang Xiaoling，Zhang Ziqiang，Li Tao，et al. Numerical simulation of effect of flux of diversion water on frazil ice evolution in diversion channel[J]. Journal of Hydraulic Engineering，2009，40(11)：10-15 (in Chinese)．

［8］ 王晓玲，曹月波，张明星，等. 辐流式沉淀池水流固液两相流三维数值模拟[J]. 工程力学，2009，26(6)：243-249.Wang Xiaoling，Cao Yuebo，Zhang Mingxing，et al.Three-dimensional simulation of solid-liquid two-phase flow in a circular secondary clarifier[J]. Engineering Mechanics，2009，26(6)：243-249 (in Chinese)．

［9］ Launder B E，Spalding D B. The numerical computation of turbulent flow[J]. Computer Methods in Applied Mechanics and Engineering，1974，3(2)：269-289.

［10］ Patankar S V. Numerical Heat Transfer and Fluid Flow[M]. New York：Hemisphere Publishing Corporation，1980.

［11］ SL 428—2008 凌汛计算规范[S]. 北京：中国水利水电出版社，2008.SL 428—2008 Ice Flood Calculation Standards[S]. Beijing：China Water Conservancy & Hydropower Press，2008 (in Chinese)．