一种提高燃料电池动态特性的新型模糊控制系统

余达太，马 欣，张 涛

(1. 北京科技大学信息工程学院，北京 100084；2. 天津大学电子信息工程学院，天津 300072)

燃料电池(fuel cell)在国外作为新型能源广泛应用在车辆及其他高污染发电工具上，随着全球原油价格的不断攀升以及空气污染和温室效应的日益加重，国际国内汽车市场对燃料电池的需求大大增加．燃料电池所使用的氢燃料可以来自于任何碳氢化合物，例如天然气、甲醇、乙醇、水的电解和沼气等[1]．

传统方法根据电化学、流体动力学、热力学等原理来对燃料电池的复杂非线性动态特性进行建模．早期的研究集中于建立用 Nernst公式、气体传播公式等来描述物理变化的稳定状态模型．近期的研究更多集中在对动态子系统进行建模[2]，通过一阶系统来管理空气压缩、惯性传导和能量守恒；进一步地研究包括结合静态和动态特性、建立时域空域模型等．这些研究的共同特点是对动态模型进行建模，但是无法表征燃料电池的非线性特性和系统响应．事实上，燃料电池内部的非线性特性及时变特性难以用系统辨识和控制的传统方法来描述，而模糊控制方法可改善传统模型的局限性．

笔者构建了燃料电池系统的辨识模型，通过建立模糊控制规则构建了一种模糊控制系统，通过仿真实验证明该方法的性能优于传统比例微分积分(proportion integration differentiation，PID)控制系统．

1 燃料电池原理

氢氧燃料电池的基本原理如图1所示．其单体电池是由正负两个电极(负极即燃料电极，正极即氧化剂电极)以及电解质组成．一般电池的活性物质贮存在电池内部，因此限制了电池容量．而燃料电池的正、负极本身不包含活性物质，只是个催化转换组件．因此燃料电池是名符其实的把化学能转化为电能的能量转换机器．电池工作时，燃料和氧化剂由外部供给，进行反应．原则上只要反应物不断输入，反应产物不断排出，燃料电池就能连续地发电．传统研究采用 Nernst公式、阳极阴极气体传播和动力学等对燃料电池进行控制策略的建模．笔者将氢气和氧气以可调整的流速形式作为输入变量输入系统，以燃料电池的功率作为输出变量[3-4]．

图1 燃料电池结构示意Fig.1 Structure of fuel cell

2 燃料电池系统辨识模型

2.1 模型辨识

模型辨识的步骤为：首先选取适当的模型形式，再确定模型的阶，最后估计模型的参数．根据燃料电池特性，笔者选用自回归(auto regression exogenous，ARX)模型[5]，它可直接利用所测的输入输出数据，反映对象的动态过程，还能方便地用于控制系统中．

ARX模型为

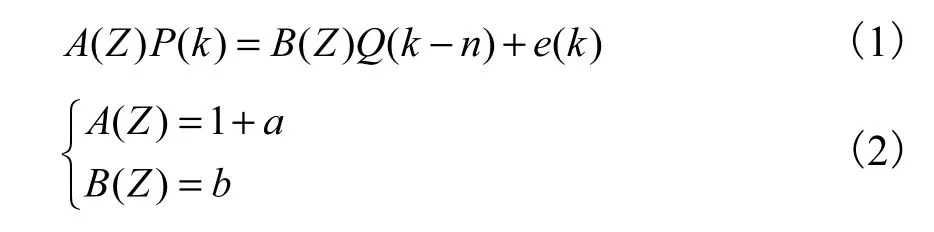
式中：()A Z为输出传递函数；()P k为输出序列；()B Z为输入传递函数； ()Q k为输入序列；()e k为误差序列；k＝1，2，…，为纯滞后拍数．为了确保燃料电池的安全性，防止谐波引起数据过大而溢出，采用诸如伪随机二进制序列作为系统激励信号[6]．

2.2 递推最小二乘法辨识

根据模型类型和结构以及筛选出来的输入输出数据，采用递推最小二乘法辨识模型参数．递归最小二乘法可利用过去的输入输出信号对系统进行预测，同时不断更新系统辨识参数．由于燃料电池具有非线性特性，递推最小二乘法可跟踪其特性变化．其中ω(k)为估计误差，在第 k步之后对数据进行更新，新的输出信号和参数计算为

式中：()ny为输出信号；()nθ为输入信号；()nφ为传递矩阵；()nu和()nω均为参数向量；()nK为估计增益，表示参数估计的相关信息； ()nP 为协方差矩阵，表示估计值和实际值之间的差异； (0)P 为初始化值；λ为遗忘因子，介于0和1之间，本文仿真实验中选取λ为0.8．

2.3 递推最小二乘仿真结果

假设输入流为氢气流速和氧气流速，输出为电池的系统功率，采用递推最小二乘法来获得系统传递函数的参数．图 2为采用二阶递推最小二乘法得到的输出功率响应，其中虚线为原始传递函数输出的功率响应，实线为采用二阶的递推最小二乘法输出的功率响应．从图中可知，递推最小二乘法可较好地反映系统特性．

图2 实时功率响应和仿真功率响应对比Fig.2 Comparison between real power response and simulation power response

3 燃料电池的模糊控制系统

3.1 模糊控制系统原理

模糊逻辑控制(fuzzy logic control)简称模糊控制(fuzzy control)，是以模糊集合论、模糊语言变量和模糊逻辑推理为基础的一种计算机数字控制技术[7-8]．它直接采用语言型控制规则，出发点是现场操作人员的控制经验或相关专家的知识，在设计中不需要建立被控对象的精确数学模型，因而使得控制机理和策略易于接受与理解，设计简单，便于应用[9]．典型的模糊控制系统如图 3所示[10]．由于能够很好地表征非线性系统，因此在燃料电池控制系统中被用来描述非线性特性．

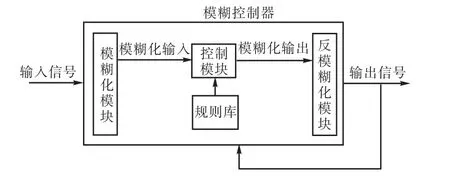
图3 典型的模糊控制系统Fig.3 Typical fuzzy control system

3.2 采用的模糊控制规则

燃料电池的动态控制是非线性控制问题[11]．可以采用实验数据来控制其输出，根据这些输入、输出数据对集合设计一个模糊系统．模糊系统采用的算法是查表法．

该系统的设计目标是设计一个对任何输入(符合规定的范围)都对应着一个输出的控制器．用V和VC来代表加载时需要的输入电压和当前设置点的电压，Δu 表示流控制的输出范围．其中 V∈[－5，5]，VC∈[－5，5]，Δu∈[－2，2]．在 V∈[－5，5]上定义 5 个模糊集，在 VC∈[－5，5]上定义 7个模糊集，如式(9)和(10)所示．它们的隶属函数的图形见图 4和图 5，其中 S3、S2、S1、CE、B1、B2、B3 分别代表负极值、负中值、负小值、零值、正小值、正中值、正极值．表1则为模糊控制器的规则库，逆模糊控制采用离散质心算法来计算．

图4 V 的隶属函数Fig.4 Membership function of V

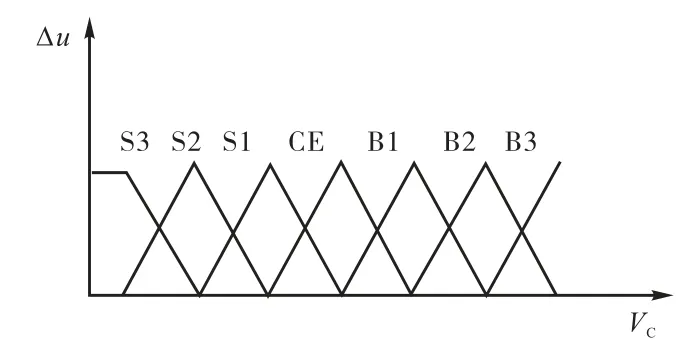
图5 VC的隶属函数Fig.5 Membership function of VC

表1 燃料电池的模糊控制规则Tab.1 Fuzzy control rules of fuel cell

3.3 仿真实验结果

传统的燃料电池动态控制大都采用常规的 PID控制．对于这样的非线性时变系统的控制效果不是很理想，主要因为常规PID控制不能根据现场的情况进行在线自我调节参数，采用本文提出的模糊控制系统可对性能进行有效的改进．图 6所示为采用传统的 PID控制方式对燃料电池进行控制器设计的仿真结果．图中横轴表示时间，纵轴表示输出功率，下曲线为典型PID控制的响应曲线，上曲线为模糊控制的响应曲线．从图中可知，模糊控制器的响应相对 PID的响应更加快速，并且更早到达稳定状态．

图6 PID控制和模糊控制响应Fig.6 PID control and fuzzy control response

4 结 语

从实验可知，相对于传统的PID控制器而言，本文提出的模糊控制器可以优化燃料电池控制响应，控制跃变过程，并使得功率泄漏较小；此外，在大型燃料电池组中，模糊控制算法相对于其他算法性能更优，负载需求增加时模糊控制的方法可以降低内部的抖动．

［1］ Ceraolo M，Miulli C，Pozio A. Modeling static and dynamic behaviour of proton exchange membrane fuel cells on the basis of electro-chemical description [J]. Journal of Power Sources，2003，113(1)：131-144.

［2］ Pukrushpan J T，Stefannopoulou A G，Peng Hei. Control of fuel cell breathing [J]. IEEE Control Systems Magazine，2004，24(2)：30-46.

［3］ Pathapati P R，Xue X，Tang J. A new dynamic model for predicting transient phenomena in a PEM fuel cell system[J]. Renewable Energy，2005，30(1)：1-22.

［4］ 戴 巍，余达太，李 果. 高尔夫燃料电池电动车电源控制系统研究[J]. 微计算机信息，2004，20(12)：83-84，88.Dai Wei，Yu Datai，Li Guo. Golf fuel cell electric vehicle power supply control system [J]. Control & Automation，2004，20(12)：83-84，88(in Chinese).

［5］ Santarelli M G，Torchio M F. Experimental analysis of the effects of the operating variables on the performance of a single PEMFC [J]. Energy Conversion and Management，2007，48(1)：40-51.

［6］ Lee Dongjing，Wang Li. Dynamic and steady-state performance of PEM fuel cells under various loading conditions [C]//2007 IEEE Power Engineering Society General Meeting. New York：Institute of Electrical and Electronics Engineers，Inc， 2007：1-8.

［7］ Hecht Nielsen R. Theory of the back propagation neural network[C]//Proceedings of UCNN. Washington，USA，1989：503-605.

［8］ Costamagna P. Transport phenomena in polymer membrane fuel cells[J]. Chemical Engineering Science，2001，56(2)：323-332.

［9］ Dutta S，Shimpalee S，Van Zee J W. Three dimensional numerical simulation of straight channel PEM fuel cells[J]. Journal of Applied Electrochemistry，2000，30(2)：135-146.

［10］ Karunarathne L，Economou J T，Knowles K. Fuzzy logic control strategy for fuel cell/battery aerospace propulsion system [C]//Proceedings of Vehicle Power and Propulsion Conference. Haerbin，China，2008：1-5.

［11］ Correa J M， Farret F A， Canha L N. An analysis of the dynamic performance of proton exchange membrane fuel cells using an electrochemical model [C]// Proceedings of the 27th Annual Conference of the IEEE．Denver，USA，2001：141-146.