基于Patran的全机柔性模型研究及模态分析
2010-07-31冯振宇王莉平
冯振宇,王莉平,王 轩,黄 彦
(中国民航大学航空工程学院,天津 300300)
全机动力学有限元模型是在全机静力分析有限元模型的基础上,按照机体结构传力路线进行简化,生成适合动力学的有限元模型。在特定情况下,为进一步简化模型,也可将整个机身直接简化为离散质量的梁单元模型,以描述机身刚度特性,梁轴为各框刚心连线,采用集中质量模拟其离散质量特性[1-3]。虽然国内外全机有限元建模的方法基本一致,但对于大型飞机来说国外的建模方法更加合理。例如,飞机上的各种结构件,杆、梁、板、壳及实体均采用更符合实际的单元体来替代[4-5]。
本文以某型无人机的几何外形建立几何模型。首先,分析简化飞机的结构,将全机分为机身、机翼及V形尾翼三大部分。然后利用MSC.Patran绘制各个结构的几何模型,并对其进行网格划分,得到全机柔性有限元模型Ⅰ。在模型Ⅰ的基础上进一步简化,将次要受力部件的质量与刚度转移到相邻结构上,仅留下主要受力部件,建立全机柔性简化有限元模型Ⅱ。利用MSC.Nastran对两个全机有限元模型进行仿真模态分析[6],得到全机各阶的固有频率和振型,再对比两个模型的结果,得到有意义的结论。
1 全机结构分析及有限元建模
本文的全机几何外形参照某型无人机绘制。在满足工程精度的前提下,对结构上进行了一些必要的简化,将主要结构简化为机身蒙皮、机身承力隔框、隔框抗剪薄板、机翼长梁、翼肋、机翼蒙皮及V形尾翼。本节将对以上几种结构进行分析并建立有限元模型。
1.1 全机结构分析
机身主要由机身蒙皮、机身承力隔框及薄板组成。机身承力隔框是飞机的主要承力构件,将承受飞行中发动机产生的推力、机翼产生的升力、蒙皮的阻力等分布力,同时也直接或间接地承受飞机其它附件的重力及惯性力。机身隔框抗剪薄板是机身主体结构的一部分,主要作用是承受剪切应力,可提高机身承力隔框整体的强度和刚度。机身蒙皮则铆接在隔框上,将机身上的气动载荷传递到隔框结构上。
机翼是飞机的一个重要结构,主要作用是产生升力,并在机翼上安装操纵面,为飞机飞行提供操纵性。飞行中,在飞机机翼上主要的外在载荷有空气动力、机翼结构质量力、部件及装载质量力等。然而这些力的合力往往不会通过机翼截面的刚心,这样机翼不仅要有抵抗弯曲应力的能力,还要有抵抗扭转剪应力的能力。特别对于大展弦比,更需有足够的强度和刚度。
V型尾翼使用两个倾斜的尾部翼面来完成和常规升降舵及方向舵结构控制面相同的功能。固定的翼面既作为水平安定面也作为垂直安定面。由于本文参照的是高空侦察机,要求结构重量尽可能轻,而采用V型尾翼则可在一定程度上减少全机的结构重量。
1.2 全机模型有限元模型及其简化模型
采用MSC.Patran逐个绘制全机部件的几何模型,形成全机的几何模型。在几何模型基础上播撒结点种子划分网格,消除重复结点,得到全机柔性有限元模型Ⅰ,如图1所示,共22 944个单元,20 871个结点。

在模型Ⅰ的基础上进行简化,除去不重要的受力结构,将质量及刚度转移到相邻结构上;除去机头及雷达整流罩,将厚度转移到抗剪薄板上;发动机进气整流罩及尾部整流罩、机身尾部的蒙皮对全机的模态影响很小,直接简化掉;除去机身内部的薄板结构,将其厚度转移到机身上;除去机翼根部的边幅及操纵面板,进一步简化机翼模型;最后得到全机柔性简化模型Ⅱ,共14 623个单元,14 246个结点,如图2所示。

1.3 全机刚度特性和质量特性的处理
建模后,对单元定义属性,其中包括各板壳单元的厚度、密度、弹性模量、泊松比。为满足弯曲刚度的要求,机翼为4梁式承扭盒。蒙皮为层压板结构,用于保证扭转刚度。
本文将两个全机模型的材料均简化为铝材,即取单元密度2.7 g/cm3,弹性模量70 GPa,泊松比0.3,单元厚度因部位不同而各异,取1.5~8 mm。从而得到全机的刚度特性与结构模型的质量特性。通过质量属性计算工具计算得到当前结构模型的总质量、重心位置及对各坐标轴的转动惯量,如表1所示。其中等效设计参数即为模型Ⅰ的质量特性参数,结构模型参数即为简化后的模型Ⅱ的结构质量特性参数。

表1 全机质量特性参数Tab.1 Quality characteristics of full-aircraft
将简化有限元模型的质量特性参数与等效设计参数比较,得到差值。运用集中质量法,将附件的质量及转动惯量集中到一点上,取质量和转动惯量的数值为上一步得到的差值,并将这一点通过多自由度约束固定到机身结构中。但在实际工程应用中,仅建立一个集中质点是不够的,需尽可能按照实际系统附件的情况,创建足够多的集中质点同时输入转动惯量。在本文中,由于无法具体确定各个附件的质量特性,因而将剩余质量及转动惯量集中到一点上,最后得到全机质量特性参数,即是表1所示的全机模型参数。
2 全机模态分析
2.1 模态分析计算理论与模态分析技术
2.1.1 无阻尼的实模态分析理论
模态是多自由度线性系统的一种固有属性,可由系统的特征值与特征矢量二者共同表示;其分别从时空两个方面来刻画系统的振动特性[8]。
本文研究的全机有限元模型为无阻尼多自由度线性振动系统,属于实模态的范畴,直接给出其系统的运动微分方程,可表示为

式中:x是位移列矩阵;M和K分别为系统的质量和刚度矩阵,它们都是n×n阶实对称阵,且M设为正定,f(t)是激励列阵。
这一系统的自由振动微分方程可表示为

其解可设为

其中:X为振幅列阵;p为圆频率;φ为初相位,它们都是待定的量。
系统的特征方程为

由此可确定p2的n个正实根,并按 pi≤ pi+1排列,i=1,…,n。pi称为系统的固有频率。系统主振型方程为

在不计任意倍数差别的意义下,可确定第i个实矢量Xi,称为系统的主振型。
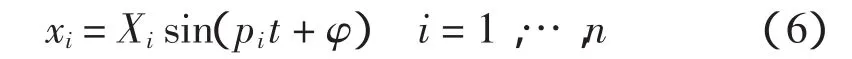
由式(6)表示的运动称为系统的主振动。可见,无阻尼线性系统的主振动都是谐振动。每个主振动有其固有的频率pi。在每个主振动中,各个位移分量振幅的相对大小与相位由主振型Xi确定。在这种情形下,系统的特征矢量都是实矢量,故也称实模态。
主振型的一个重要性质是正交性,根据其可通过实模态变换来使式(1)表示的系统解耦。理论证明一个n自由度的无阻尼线性系统的响应问题,通过实模态变换,可转化为n个独立谐振子的模态响应问题。
2.1.2 全机模态试验技术
模态分析提供了研究各种实际结构振动的一条有效途径[9]。首先,将结构物在静止状态下进行人为激振,通过测量激振力与振动响应并进行双通道快速傅里叶变换(FFT)分析,得到任意两点间的机械导纳函数。用模态分析理论通过对试验导纳函数的曲线拟合,识别出结构物的模态参数,从而建立结构物的模态模型。全机模态试验技术与一般结构模态试验技术不同的是,全机模态试验要求自由支持,自由支持意味着试验物体在任何坐标上都不与地面接触。实际上,要提供一个真正的自由支持是做不到的,通常则由柔性支撑或悬挂装置提供一个非常接近自由支持条件的悬挂装置。而在Patran中不需要模型定义任何约束,即可直接计算其在自由支持的模态参数。
2.2 模态计算结果
2.2.1 模型Ⅰ的模态计算
运用MSC.Nastran提供的实特征值求解方法对全机的MSC.Patran模型进行解算,采用求解精度较高的Lanczos求解法,能保证在大型结构特征值求解中不会失根,也就保证了全机动态特性有限元分析的完整性。理论上系统的固有频率数目与其自由度一致,本文选择求解根数为50并提交给MSC.Nastran进行运算,得到模型Ⅰ各阶的固有频率及振型。除去结果中的前6项刚性模态,选取前8阶和第40、41阶模态,各阶振型和固有频率如表2所示。

表2 模型Ⅰ固有频率计算结果Tab.2 Natural frequency of FEMⅠ
再将MSC.Nastran的运算结果导入MSC.Patran进行后处理得到可视化图形,全机模型Ⅰ前8阶和第40、41阶的振型位移云图如图3所示。
2.2.2 模型Ⅱ的模态计算
现在计算模型Ⅱ的模态,操作方法和步骤与模型Ⅰ的相同,仍旧采用Lanczos法求解计算其前50阶的模态。除去结果中的前6项刚性模态,选取前8阶和第40、41阶模态,各阶振型和固有频率如表3所示。

再将模型Ⅱ的运算结果导入MSC.Patran进行后处理得到可视化图形,全机模型Ⅱ前8阶和第40、41的阶振型位移云图如图4所示。
2.3 结果分析
2.3.1 共性分析
从图3、图4可以直观地看出振动变形主要集中在机翼和尾翼上。而机翼是飞机产生升力的主要结构,同时和尾翼一起工作为飞机提供操纵性。两者结构刚度的不足对飞行的安全性和操纵性有很大的影响。这也从侧面反映了高模复合材料在飞机结构上的巨大作用。

表3 模型Ⅱ固有频率计算结果Tab.3 Natural frequency of FEMⅡ

在模型建立时,为了方便计算,将全机有限元模型简化为铝质材料,设定其弹性模量为70 GPa,但实际上飞机的主体材料都是复合材质,其弹性模量高于铝质材料。因此,表1、表2的结果所示,全机的固有频率普遍偏低。
2.3.2 差异性分析
将表1与表2对比可看出,模型Ⅱ的整体固有频率要高于模型Ⅰ的,模型Ⅱ的模态更符合实际情况。主要原因是模型Ⅱ在模型Ⅰ的基础上做了合理简化,模型Ⅱ去除了一些不重要的结构,将质量及刚度转移到相邻结构上,并按照受力原则提取主要的承力结构。对于复杂有限元系统来说,尽管模型逼真,但过于复杂的结构往往会使部件间的刚度差距过大,计算出的高阶模态通常都是局部模态。模型Ⅰ的高阶模态混杂大量的局部振型,而模型Ⅱ却能保持全机的高阶振型,不会在高阶失去全机模态。这说明准确建模是非常重要,工程实用的有限元模型应该同时具有力学的完整性和模型的简洁性。
3 结语
本文介绍了基于Patran软件的全机各结构简化的原则,研究建立了全机柔性有限元模型及其简化模型。基于Nastran解算器,运用模态分析方法对模型进行了模态分析,由于全机模型Ⅰ过于复杂,计算生成的高阶模态掺杂大量无用的局部振型,而简化的全机模型Ⅱ在高阶模态上有较完整的全机振型。分析表明全机的固有频率偏低,容易发生共振,其主要原因是材料的弹性模量偏低,容易发生共振。但理论分析可知全机固有频率的二次幂与结构刚度成正比,与结构质量成反比,结构的刚度是由材料自身的属性及几何尺寸决定的。因此简化假设并不影响本文工作的实际应用,只需要改变材料的属性,本文提出的柔性有限元模型和其简化模型的建模方法以及模态分析的思路即可应用于工程实际。
[1]王彬文.大型飞机全机地面振动试验技术研究[J].结构强度研究,2007(4):29-44.
[2]韩普祥,秦瑞芬,凌爱民.直升机全机动态特性有限元分析[J].直升机技术,2001,128(4):9-12.
[3]张凌霞,齐丕骞,马晓利.飞机结构动力学有限元模型修正[J].结构强度研究,2007(4):23-28.
[4]HAUKE GUELZAU.Flexible Multi-Body Modeling and Simulation of Flap Systems in Transport Aircraft Determination of Dynamics and Failure Loads[C]//California,MSC.Software VPD Conference,2006.
[5]XU ZE.Digital Simulation of Full Scale Static Test of Aircraft[J].Chinese Journal of Aeronautics,2005,18(2):138-141.
[6]柳永波,冯振宇.基于MSC.Nastran的机翼有限元颤振分析[J].中国民航大学学报,2007,25(s1):48-49.
[7]陈绍杰.复合材料与无人飞机[J].高科技纤维与应用,2003,(2):31-33.
[8]方 同,薛 璞.振动理论及应用[M].西安:西北工业大学出版社,2002.
[9]吴 森.结构试验基础[M].北京:航空工业出版社,1992.
