图论最大流理论在机场登机口分配中的应用

2010-07-31李明捷蒋凤伟

中国民航大学学报 2010年5期

李明捷，石荣，蒋凤伟

（1.中国民航飞行学院 a.空中交通管理学院；b.飞行技术学院，四川广汉 618307；2.四川省机场集团有限公司，成都 610200）

随着机场航班日起降架次的增多和乘飞机出行旅客数量的迅速增长，现有的登机口资源正面临着日益严峻的考验。目前，大多数机场通过借鉴其他机场的做法，或根据以往的经验来进行登机口分配和调度，往往导致很多载客数量较多的大中型飞机停靠在距安检或者行李提取大厅较远的登机口；或由于远、近机位登机口航班密度安排不合理，使得每个登机口的航班组合没有达到最优，从而降低了登机口的利用效率。

对于中国大多数中小型机场来说，由于航班日起降架次相对较少、到离港时间相对分散，故在机场运行资源分配和优化问题研究时，学者们多将目光集中在停机位资源优化与分配问题上，而较少考虑登机口的分配和调度优化方法。南京航空航天大学的王志清等人将图论应用到登机口分配问题中，提出旅客登机口调度优化网络模型，具有一定的创新性，模型假设进、出港旅客步行距离基本相等，没有考虑中转旅客对登机口分配的影响[1]。南京航空航天大学的曹燕在其硕士学位论文中利用表上作业法对登机口分配模型进行了考虑，但直观性不强[2]。中国民航飞行学院文军等人将图着色模型应用到机位分配中，使图论的思想在资源分配中得到应用[3]。但在考虑登机口分配问题时，由于近机位登机口与近机位一一对应，因而可以用机位分配与优化模型来模拟登机口的分配；而远机位登机口具有一定的特殊性，对于旅客而言，登机口与机位是一一对应的关系，但从空间分布上来看，其可以是一个或几个登机口对应一个或多个机位的设置形式，也就是“一对多”或“多对多”问题，此时若再使用停机位的分配与优化方法来解决登机口的分配就不合理了。

本文以进、出港旅客总的步行距离最短为主要优化目标，运用图论中的网络最大流理论来解决登机口的分配与优化问题，在保证机场安全、高效运行的前提下，尽可能提高登机口利用效率，体现民航旅客运输的便捷性与舒适性。

1 研究与方法

1.1 旅客步行距离最短模型的优化目标与约束条件

1.1.1 优化目标

1）使进、出港旅客的总步行距离最短，满足旅客对航空运输“便捷性”的需求；

2）使现有设施使用效率达到最高，优化资源配置。

1.1.2 约束条件

1）机型与机位类型相匹配；

2）分配登机口时，一个航班必须被分配且仅能被分配至一个登机口；

3）应满足最短过站时间和同机位安全间隔时间的要求；

4）“航班对”的限制：由于在机场停靠的绝大部分航班既担负着进港航班任务，又担负着出港航班任务，因此，尽量将此类飞机尽可能安排在同一个登机口，降低航空公司运营成本。

除此之外，根据各机场的性质和特点不同，还需考虑登机口分配的优先原则、航班过夜、飞机维修等约束条件[1-4]。

1.2 旅客步行距离最短模型的设置条件

1.2.1 假设条件

假设某机场有m个可用登机口，当日有n个航班，每个登机口的启用和停用时间、每个航班的载客人数均已知。根据某机场一天中部分时段的航班计划，将各航班信息汇总如表1所示。

1.2.2 航站楼布局对登机口分配的影响

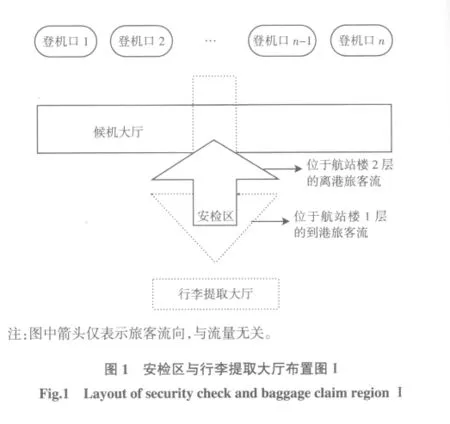
当登机口位置布局已知，则安检区和行李提取大厅的位置将会直接影响到进、出港旅客步行距离的长短。这里所讲的航站楼布局，主要分为两种：一是安检区与行李提取大厅位于航站楼上、下两层中基本相同的位置；二是安检区与行李提取大厅位于航站楼上、下两层或同层中不同位置。

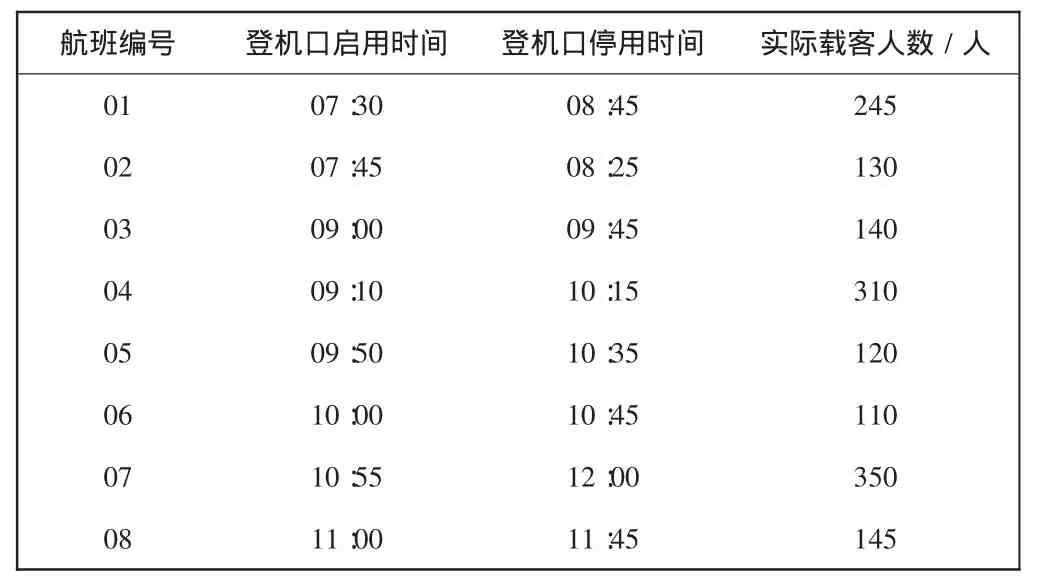
表1 某机场一天中部分时段航班信息汇总表Tab.1 Flight information table of an airport in the part time during a day

1）安检区与行李提取大厅不同层但位置相近

对于大部分机场而言，进、出港旅客总人数总体来讲近似相等，对于图1[4]这种设置方式，虽然进、离港旅客的行走路径不同，但一般情况下，在进行登机口优化分配过程中可将进、出港旅客步行距离视为相等，在进行登机口分配时，需按照航班实际载客人数，尽量将人数较多的航班安排在靠近安检区的登机口。

2）安检区与行李提取大厅（不）同层且位置不同

对于某些中、小机场，其安检区与行李提取大厅采用同层或分层且相隔较远的方式设置，如图2[4]所示，在这种情况下，应根据航班人数，结合其他限制条件进行登机口分配。

2 结果与分析

2.1 数据收集与整理

本文利用表1中已知航班信息作为实例分析的数据来源，采用最广泛的航站楼布局形式，即假定安检区和行李提取大厅分别位于航站楼的上、下两层，位置近似相同，以此来说明该模型的构建方法和应用过程。

2.2 优化分配网络模型的构建

2.2.1 进、出港旅客步行距离最短模型建立与实证分析

对于国内大部分干线和支线机场而言，始发或终到旅客所占比例甚多，从长时间的数据统计来看，这两部分旅客所占比例相当，因此，可将其步行距离视为近似相等。以下就是进、出港旅客步行距离最短模型的实施步骤：

步骤1 按照登机口启用时间的先后顺序，由左至右把每个航班作为网络图上的一个节点，在考虑各种约束条件的基础上，将节点之间进行有向连线，方向为由离港时间早的航班指向晚的，由此形成一个由节点和箭头构成的网络图。不难理解，网络图中从起点到终点的每一条有向路径上的节点都是可以安排在一个登机口上的航班组合，如图3所示。

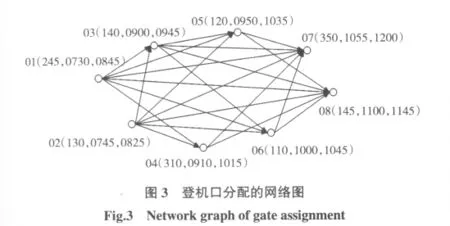
步骤2 在图3上，按照各节点的时间顺序对其进行二次编号G（A，B），G表示航班编号；A表示航班G的前一个航班的编号（若为起始航班，则其编号为本次航班的号码）；B表示航班载客人数的累计，即前一个航班A的实际载客人数与本次航班G的实际载客人数之和。需要注意的是，若A前有两个或多个已编号航班，则择选B最大的那个航班作为G的前一个航班，如图4所示。

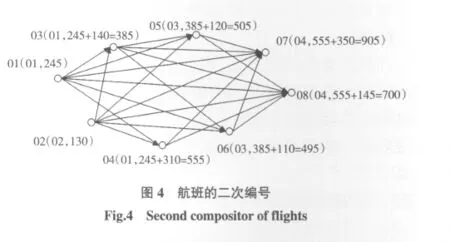
步骤3 将每架航班的人数看成是网络图中的流量，从登机口结束使用的这个网络图的最大流量就表示可以使用同一个登机口的人数最多的航班组合。从终点开始逆向寻找一条至起点航班人数最多的路径，并把这条路径上的航班安排在距安检出口最近的登机口。在图4中，01→04→07即为该网络图中旅客流量最大的航班组合，可将这3个航班按照登机口启用先后顺序安排至离安检区最近的登机口。

步骤4 在调度网络图上去掉已安排过的航班节点及与其相关联的箭线，再从新的起点开始寻找一条至终点航班人数最多的路径，并把这条路径上的航班安排在距安检出口次近的登机口，如图5所示。在图5中，02→03→05→08为网络图中旅客流量最大的航班组合，可将这4个航班按照登机口启用先后顺序安排至离安检区次近的登机口。

步骤5 重复步骤4，按照上述方法直到所有的航班安排完为止。本例中剩下06号航班，可将其安排至3号登机口。

2.2.2 中转旅客步行距离最短模型

对于大型枢纽机场以及部分干线机场而言，国际转国际、国际转国内、国内转国内的中转旅客数量较其他中小机场多。中转旅客的流程大致可以概括为：旅客下机→中转柜台→中转休息厅→安全检查→登机，中转旅客的所有中转过程都在隔离区内完成，旅客不用出去重新办理登机手续。则中转休息厅相对于安检区的位置将直接决定中转旅客在航站楼内步行距离的长短。假设该段距离长短已定，则需考虑登机口与安检区的相对位置，以便尽量减少该部分旅客的步行距离。

具体分配的思路是：根据进、出港旅客步行距离最短模型的分配结果，利用网络最大流理论，考虑在航班间隙将中转旅客流量最大的航班安排在距离安检区最近的登机口，以此类推，具体过程参见本文的2.2.1节。

2.3 算法复杂度分析和最优性证明

2.3.1 算法的复杂度分析

如前所述，该模型总运算次数不会超过n，而网络图中航班节点的总数也不会超过n，故总运算次数不会大于 n2，即其计算复杂度为 o（n2）。

2.3.2 算法的最优性证明

为了说明算法是最优算法，现在登机口调度网络图上增加一个虚拟起始节点s和一个虚拟终结节点t，并将虚拟起始节点s与所有起始航班节点用箭头相连，同样，将所有终结节点与虚终结节点t也用箭头相连，如图6所示。

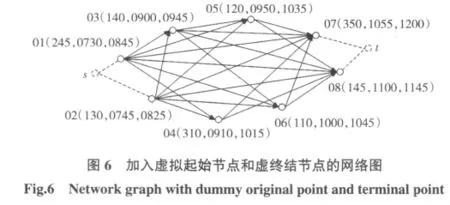
由于各航班节点是按时间顺序由左至右排列的，因此，图6所示的网络图是一个具有两端点s和t的无环路网络图。其中每一条从s到t的有向路径，都是可在同一个登机口安排航班组合的可行方案。如果把各节点的航班人数作为以该节点为终点的各箭线的权值，则该网络图就相当于一个双代号计划网络图，而上面的算法等同于在此双代号网络图中寻找从s到t的最大权值路线的算法[5]。因此，当各箭线的边权值为该箭线指向节点的航班乘客人数时，所形成的最长路线就是可以安排在同一个登机口的乘客人数最多的航班安排组合，由此印证了该算法的最优性。