基于QAR的PW4077D发动机放气活门与N1的关系

曹惠玲，宋 强

（中国民航大学航空工程学院，天津 300300）

飞机在飞行过程中，需要根据自动控制原理运用机械、液压、气动、电动等控制装置，使航空发动机自动地按预定规律工作，以便发动机在各种飞行条件下都能安全工作并获得最佳或接近最佳的性能。这些预定的规律直接关系到发动机的性能指标，也是实现发动机控制的最基本最重要的内容。因此，对发动机在飞行过程中的特性参数控制规律的研究具有非常重要的意义。目前，民航发动机均为国外制造，发动机放气活门的详细控制规律属于保密技术。中国民航业只有根据飞机的维修手册、飞行数据等材料，对影响控制规律的一些因素定性了解，对于许多特性参数控制规律还未能建立比较完善的模型，未能掌握其预定的控制规律。随着对QAR数据的深入分析，可以发现其中蕴含了极为丰富的发动机控制规律的信息。

本文由此出发，选取国内某航空公司B777飞机的PW4077D发动机为研究对象，以2.5级放气活门控制规律为主要研究内容，以期为发动机状态监控和性能分析提供有价值的参考依据。通过对QAR数据相关性分析后发现，2.5级放气活门开度大小的调节是一个较为复杂的过程，取决于很多因素，如低压转子转速N1、飞行高度、飞行马赫数、油门杆角度等，但与N1的变化关系最为密切，且变化趋势明显。为保证能够较为准确反映活门开度控制规律的同时，避免分析过程过于纷繁复杂，故仅选定N1一个参数为自变量，研究其与活门之间的变化规律，作为后续研究的基础或参考。其他影响活门开度大小的参数本文暂不予讨论。

1 QAR数据修正

QAR（quick access recorder）作为广泛采用的数据记录装置，原始忠实地记录了来自飞机各系统的大量运行参数，连续完整地反映各飞机系统在运行中的实际状态或失效的征兆信号，为分析和排除飞机故障提供强有力的帮助，同时也为分析飞机性能、实现状态监控提供了最重要的原始数据。但不同航班，飞机所经历的外界条件（主要为外界总温、总压）千差万别。根据航空发动机原理可知，同一台发动机在不同的工作条件下，其主要性能参数差别很大，所以不同航班的原始性能数据通常无法直接用于相互比较分析。针对这一问题，相似理论给出了很好的解决方法，用于消除外界条件对发动机性能参数的影响。

相似理论指出：在几何相似的前提下，一台发动机或几台不同的发动机在各种各样的条件下工作时，如果对应截面上的同名物理量的比值分别相等，则称发动机的这些工作状态是相似的。整台发动机工作状态相似的充分必要条件是：飞行马赫数和换算转速守恒，即

式中：n1为实际转速；Tt2为压气机进口总温。

根据上述航空发动机相似理论，可将N1修正至统一的大气条件下，从而消除了外界条件对发动机性能参数的影响，增强不同航班间数据的可比性。通过参考相关资料以及相似理论的有关推导，得出低压压气机转子转速N1的相似修正公式为

式中：下标raw表示原始数据；下标cor表示修正后的数据；N1为低压转子转速（%RPM）。

航班飞行中除外界条件的差异外，飞行中所用推力也会影响发动机性能参数值。普惠公司的发动机主要采用EPR表征推力值。由于不同航班巡航状态机组所取推力值不同，同一台发动机性能参数，即使进行了相似修正也不能完全具有可比性。所以为实现不同航班巡航数据的比较，必须根据发动机基线将数据进行功率修正，换算成为相同的EPR下的性能参数，这样才能最终实现数据的对比。根据普惠公司的EHM手册，得到具体的修正公式为

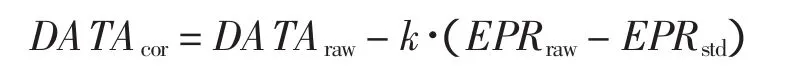
式中：DATAraw为修正前数据；DATAcor为修正后数据；EPRraw为实际推力值；EPRstd为设定的标准推力值；k为DATAcor与EPR的斜率关系。

以上给出了对不同航班、同一类型发动机的QAR数据进行统一修正的方法，数据修正后进行下一步数据建模工作[1－2]。

2 数据建模

2.1 数据点分段

每个航班的QAR数据数量较大，平均为10 000条左右，每1 s记录1条数据。同时QAR系统在采集数据时也会受到一些随机因素的影响。为使数据拟合得更为准确，通过比较各种平均化方法的优缺点以及本研究使用数据的特点，选择采用了算术平均数的方法对数据进行初步的平均处理。这种方法不仅能消除样本数据中一些随机因素的影响，而且能满足样本数据点之间没有权重差别的特点。具体方法如下：

1）把解码后的数据按照N1转速的大小（%RPM）从0～100，以1个百分比为单位，均等划分所有数据点，即划分成100个数据组；

2）分别把每个数据组中的放气活门开度SEL25BP（%）进行算术平均化处理，得到对于不同区间的代表数据值。

这样处理后，运用各种方法拟合出的模型的样本相关系数和相关系数平方值都比较高，由数理统计知识表明拟合效果良好。所有数据都处理完后，在直角坐标系中标出所有点，如图1所示。其中：纵坐标为2.5级放气活门开度SEL25BP（%），横坐标为发动机低压转子转速N1（%RPM）。

由图1可大致看出活门开度大小随N1的变化特点：发动机低速时，活门开度最大；发动机加速时，活门开度明显变小；当发动机处于巡航状态或持续爬升状态，活门开度降为最小。这一变化情况与发动机的实际运行是相符的。因此，在建模前将变化情况分为3个阶段：

1）N1转速从1%～40% 在这一阶段发动机处于慢车状态或打开反推状态，放气活门开度变化较小，稳定在全部打开状态，SEL25BP≥92%，不随N1的变化而变化。此阶段发动机转速较小且明显偏离设计值，从而使压气机增压比较小，空气流量系数不高，气流与叶片攻角较大，发动机容易发生喘振。同时，此阶段飞行高度低，大气温度高，进口处气流总温较高，空气难以压缩，也造成了增压比的减小和压气机流量系数的变小，气流攻角增大，容易诱发喘振。因此，需要完全打开放气活门，通过改变进口处空气流量来改变工作叶轮进口处绝对速度的大小，从而改变其相对速度的大小和方向，改变攻角大小，达到防喘的目的。

2）N1转速从40%～86% 这一阶段发动机处于明显的加速或减速状态，持续时间短，数据点少。活门开度变化较大，并且趋势明显，与N1近似呈线性变化关系。与上一阶段相比，此阶段随着转速的上升，压气机增压比逐渐增大，空气流量系数变大，气流与叶片的攻角减小，发动机逐渐脱离喘振边界。同时，飞行高度不断上升，大气温度变低，进口处气流总温降低，空气密度变大，也使增压比和流量系数有不同程度提高，气流攻角减小，所以，此阶段为达到防止喘振的同时又保证发动机的工作效率，放气活门只需部分打开，并随转速的不断提升，放气活门打开角度逐渐减小。

3）N1转速从86%～100% 这一阶段飞机处于爬升或巡航阶段，低压转子转速较高，2.5级放气活门稳定在全闭状态，SEL25BP≤1%，不随N1的变化发生变化。此阶段发动机转速处于或接近处于发动机的设计转速，飞行高度高，进口处气流密度大，总温低，保证了压气机的增压比和流量系数，从而保证了叶片的攻角，不易诱发喘振。同时，在此阶段N1转速处于最大推力转速左右，为保证较高的工作效率和较低的燃油消耗率，也要求放气活门处于完全关闭状态。

2.2 数据建模

由于2.5级放气活门开度在上述划分的3个阶段中变化情况各不相同，第1、第3阶段并不随N1转速的变化而发生变化，故在建模过程中，仅对第2阶段采用数理统计学的一元线性回归、一元非线性回归（包括幂函数、指数函数、对数曲线、二次多项式）方法进行拟合。在模型建立后对这些模型的最优性进行比较，并选出最优数学模型。由数理统计理论，可得数学模型判断标准如下：

1）检验各种方法能否通过F检验。

a）提出假设：原假设 H0∶β1=0；备择假设 H1∶β1≠0。

b）给定显著性水平α，查F分布表获得临界值Fα（1，n－2）。

c）根据

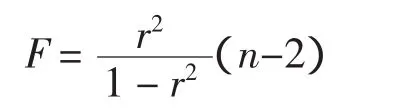
式中：r2为相关系数平方值。利用样本数据计算检验统计量F的值。

d）进行比较，做出判断。

若F＞Fα（1，n－2），差异显著，拒绝原假设，接受备择假设；若F≤Fα（1，n－2），差异不显著，接受原假设。如图2所示。

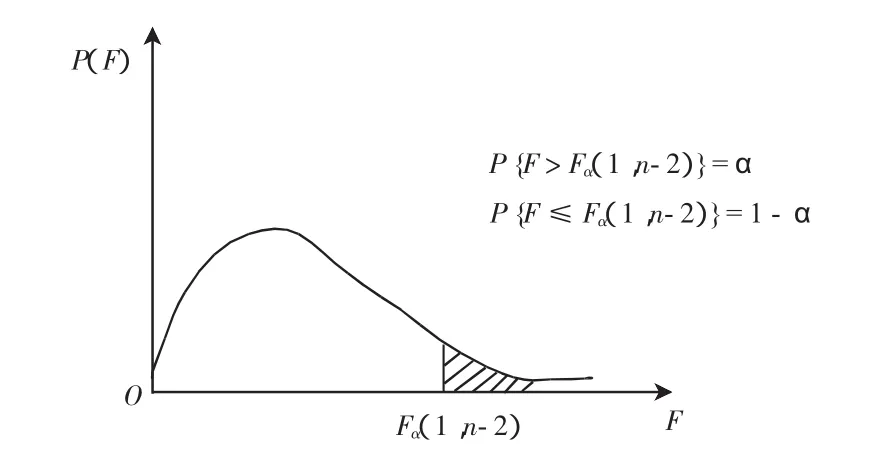
图2 F检验的否定域指示Fig.2 Chart of negative extent of the F-Test

2）比较R2（样本相关系数平方值）的大小。它是最常用的回归拟合优度度量，表示由回归模型做出解释的变差在总变差中所占的比重，即

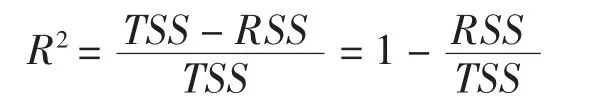
式中：RSS为残差平方和；TSS为总离差平方和，即残差平方和与回归平方和之和。

参照相关数理统计理论，由上式可知：若样本剩余RSS越小，R2的值就越大，拟合优度越好；反之，RSS越大，R2的值就越小，拟合优度越差。

3）在以上两个数都相差很小的情况下，残差平方和RSS的大小（越小越好）可以作为进一步的判断方法，最后确定最优模型。

通过以上检验和比较，确定出该型发动机2.5级放气活门开度与N1两者最优数学模型为

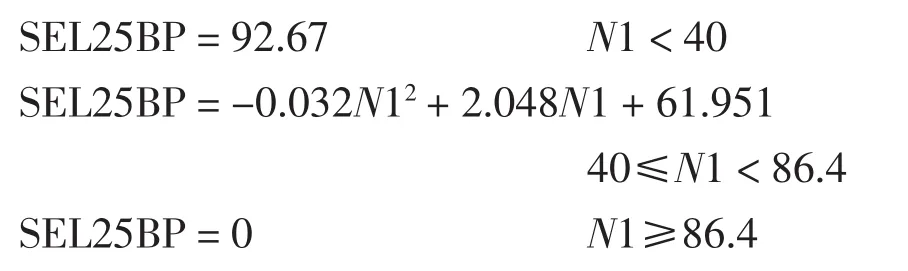
式中：SEL25BP为发动机2.5级放气活门开度（%）；N1为低压转子转速（%RPM）[3－5]。

3 模型验证

此数学模型是使用某航空公司4台在翼发动机共10个航班的数据拟合建立，不足以代表所有该型发动机2.5级放气活门开度与N1两者之间的变化情况，因此还需对数学模型进行校验，以确定模型的准确性。

使用该机队与建模数据不同航班的数据来检验此数学模型。校验模型采用的方法为：

1）在建立的数学模型中代入所用验证航班修正后N1值，计算出相应的2.5级放气活门开度预测值；

2）比较SEL25BP预测值与实际发动机QAR数据中SEL25BP值的大小，计算出预测值与真值间的偏差；

由于篇幅有限，航班数据点个数有10 000多个，在此不再罗列校验航班中各个数据点具体的偏差值大小，仅用图表形式表示拟合效果，如图3所示。

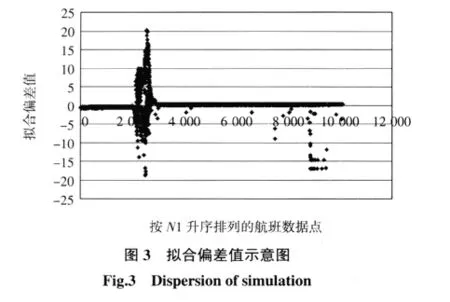
由图3可知，数据拟合偏差较大处发生在横坐标第20 000～30 000数据点之间，且相对集中。在此阶段，对应的修正后N1值范围为65%RPM～75%RPM，与图1中曲线的不平滑段相对应。由于图1是由10个航班数据处理后所得，所以此不平滑段有较强代表性。由发动机的工作原理和控制规律分析可知：

1）数据拟合偏差较大的不平滑段正处于飞机爬升或降落阶段，通过查阅该型发动机客户维修培训手册等相关资料知，飞机在低空和高空两种状态转化时，发动机系统的气动参数调节有一个系统滞后的过渡带。这是造成拟合偏差较大和图1中散点图不平滑段的原因之一。

2）在此阶段EEC指令调节2.5级放气活门开度大小时，飞行高度、飞行马赫数、油门杆角度等参数也对活门开度的调节起到了较大作用，此时仅用N1转速作为调节因素做数据拟合，就造成了较大的偏差。

3）QAR数据显示，此阶段多处出现2.5级放气活门开度的突变情况，不再是简单的线性或非线性变化，这也在很大程度上造成了数据拟合的较大偏差。根据文献[6]可知，在按照相似转速程序控制的压气机中，活门开度的调节分为瞬态调节和稳态调节，根据转速的变化率来区别发动机是快减速还是慢减速，从而决定对放气活门使用瞬态或稳态开关点，开关点的不同，造成了QAR数据上的“回程差”，此种现象在按照EEC指令控制的压气机中也有明显体现。这也是此不平滑段数据拟合偏差较大的一个原因。今后可将航班划分为不同的小段，详细分析各小段的参数变化情况，从而更精确地得出2.5级放气活门的控制规律。

除此之外，其他阶段拟合偏差较小，拟合效果良好。综上所述，拟合出的数学模型在一定程度上较好地反映了2.5级放气活门开度大小的控制规律[6－8]。

4 结语

飞机在飞行过程中要经过多种状态之间的改变，正是由于发动机工作状态的多变性，为保证工作效率并及时防止喘振，2.5级放气活门的开度就必然要面对多种情况下的调节，从而形成了一套较为复杂的调节规律。本文着眼于化繁为简，仅就一个影响因素进行分析。运用发动机的历史数据来探索发动机气动参数的控制规律，运用拟合建模的方法较好地反映了目标参数的大体变化情况，为后续更进一步的研究提供了有价值的参考。最后使用新的航班数据对模型进行验证，在验证结果并不十分理想的个别航段，本文进行了一定程度的原因分析，为更深一步的探索指明了方向。在其他航段，拟合得到的数学模型具备了较高的准确性，能够很好地反映出该型发动机气动参数的控制情况，对实际的工程工作具有一定的参考价值。

[1]Pratt&Whitney Company.ECMⅡ Training Manual[G].USA：Pratt&Whitney Company，1994.

[2]Pratt&Whitney Company.PW Engine Monitoring Program[EB/OL].（2008－07－08）.[2001－04－01].http：//www.pratt－whitney.com/serv_comm_main_monitor.asp.

[3]ANDERSON T W.Introduction to Multivariate Statistical Analysis[M].3rd ed.New York：John Wil&Sons Inc，2003.

[4]吴 诩，李永乐，胡庆军.应用数理统计[M].北京：国防科技大学出版社，1995：135－161.

[5]张文彤，董 伟.SPSS统计分析高级教程[M].北京：高等教育出版社，2004.

[6]许春生.民用航空发动机控制[M].北京：中国民航出版社，1995.

[7]瞿红春，林兆福.民用航空燃气涡轮发动机原理[M].北京：兵器工业出版社，2006.

[8]廉小纯，吴 虎.航空燃气轮机原理[M].北京：国防工业出版社，2000.