附着全钢升降脚手架不同步升降性能研究
2022-08-01杨伟
杨 伟
(中铁十八局集团建筑安装工程有限公司, 天津 300308)
附着升降脚手架因综合了挑、吊、挂式脚手架的优点,具有受建筑高度限制小、装拆效率高、施工成本低、美观环保等多个优势,现被广泛应用于高层及超高层建筑施工过程中[1-2]。
附着升降脚手架通常采用电动葫芦进行升降,由于电机转速差异、提升点重量不同、电路故障等原因,各机位会形成升降高差,导致某些提升点失载或超载,易发生安全隐患[3-6]。
岳峰等对附着升降脚手架的基本设计计算规定和具体设计计算方法作了系统讨论,给出了主要承重结构按概率理论为基础的极限状态设计方法的基本表达式[7]。杨光祥等基于测量电动葫芦电机转数的同步控制方法,利用微动开关对电机的转速测量,间接计算脚手架升降的高度差,从而实现各个机位的同步运行[8]。目前,对附着升降脚手架的构造研究较多,而对其力学性能与设计方法研究较少,尤其是升降不同步效应及其考虑不同步效应的设计方法尚无涉及。
本文通过对附着式升降脚手架的足尺试验和大量的参数化数值模拟,研究了不同步效应,提出了考虑不同步效应的设计方法,可为附着式升降脚手架的标准编制提供技术支撑。
1 试验研究
1.1 试验模型参数
试验模型如图1、图2所示。架体长16.0 m,高13.5 m,层高2 m,相邻立杆纵向跨度2 m,内外立杆跨度0.6 m,搭设7步。架体采用电动葫芦中心提升机,功率为500 W,额定荷载为75 kN,提升速度为120 mm/min。

图1 附着升降脚手架试验模型实物Fig.1 The attached lifting scaffold for experiments

图2 附着升降脚手架试验模型正视Fig.2 The facade of the attached lifting scaffold for experiments
1.2 测点布置
在架体内侧从左至右依次设置A、B、C、D四个机位,AB、BC、CD机位之间跨度分别为6 m、6 m、4 m,如图3所示。设置8个应变测点,按顺序分别为:横向水平杆SC-1、纵向水平杆SC-2、刚性支架SC-3、水平桁架横杆SC-4、水平桁架斜杆SC-5、主框架立杆SC-6、副框架立杆SC-7、导轨SC-8。各架体构件材料参数见表1。

图3 应变测点布置 mmFig.3 Arrangements of the strain measuring points

表1 架体构件材料参数Table 1 Material parameters of the frame structure mm
1.3 试验数据分析
试验之前,将各机位进行调平,使其处于同一水平高度。当提升此架体1 000 mm后,发现仅端部机位A不同步,其超升了5 mm。随着架体逐渐被提升,8个测点所在的主要受力构件的应力发生起伏变化;提升完毕后,机位A附近构件的应力最大增加3.5 MPa,机位B附近构件的应力最大增加4.0 MPa,如图5所示。

a—机位A附近构件; b—机位B附近构件。图5 上升阶段应力时程曲线Fig.5 Stress time-history curves in the lifting phase
对各机位进行调平。当下降此架体1 000 mm后,发现机位A、D不同步,两者都滞后了6 mm。如图6所示,随着架体逐渐被下降,8个测点所在的主要受力构件的应力也将发生起伏变化。下降完毕后,机位A附近构件的应力最大增加到4.5 MPa,机位B附近构件的应力最大增加到5.0 MPa。
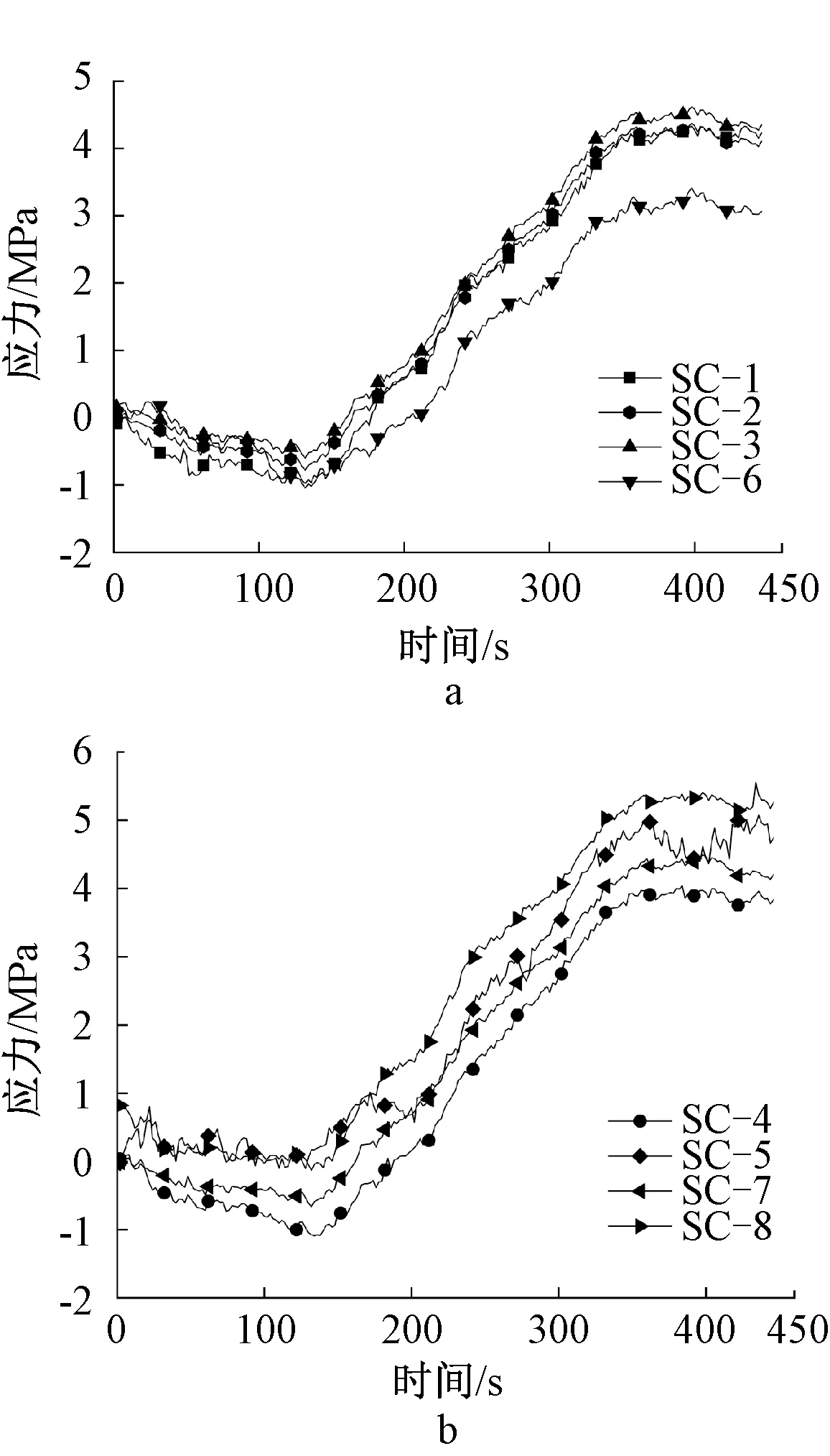
a—A机位附近构件; b—B机位附近构件。图6 下降阶段应力时程曲线Fig.6 Stress time-history curves in the falling phase
在此试验中,认为提升机是匀速运动的。根据位移变化量(最高机位与最低机位之间的高度差)和运动时间的线性关系,结合试验过程中相应的应力-运动时间曲线,绘制应力-位移变化量曲线,如图7所示,以便于验证数值模型。

a—机位A超升; b—机位A、D滞后。图7 升降阶段应力-位移变化量曲线Fig.7 Stress-displacement curves during operation
2 数值模拟分析
2.1 建立数值模型
本文采用ABAQUS软件建立数值模型。架体杆件、导轨圆钢采用B31单元,脚手板和导轨其他部分采用S4R单元。材性试验测得弹性模量E=209 GPa,屈服强度fy=270.1 MPa,抗拉强度fu=431.5 MPa,泊松比μ=0.28。脚手架处于升降阶段时,支顶器对架体无约束,架体通过提升动力设备进行升降。由于防倾装置的存在,限制了导轨在x、z方向的平动和转动,保证各机位运动过程中架体不会发生倾覆。数值模型如图8所示。

图8 有限元模型Fig.8 The finite element model
2.2 数值模型验证
在单机位A超升5 mm的模拟试验中,将其他机位进行固定,给予机位A向上的荷载,直至位移达到5 mm。同理,设计双机位A、D滞后6 mm的模拟。
通过数值分析,得到上述两组模拟试验在各测点位置处的应力变化值。如表2所示,各测点处的应力变化量模拟值和试验值的误差在20%以内,试验和数值模拟得到的结果吻合较好,证明采用数值模拟能够较为合理地反映实际升降不同步响应的结果。

表2 模拟值与试验值对比Table 2 Comparisons between the simulated values and the experimental values
3 参数化分析
在实际施工时,附着升降脚手架的机位可能会出现超前或滞后的运动情况。在JGJ 202—2010《建筑施工工具式脚手架安全技术规范》中第4.7.3条规定:各相邻提升点间的高差不得大于30 mm,整体架最大升降差不得大于80 mm。
为观察不同机位间位移差值引起机位荷载的变化,需充分考虑整个架体受到各工况的影响。模拟中可将各机位运动工况分为:单机位不同步运动、双机位不同步运动和三机位不同步运动,共计32个工况。
3.1 单机位不同步升降工况
表3列出了单机位不同步运动工况的基本方式,共4种工况。在工况1模拟试验中,固定B、C、D机位,给予机位A向上的位移,直至位移变化量达到80 mm。同理,设计工况2~4的模拟试验。

表3 单机位不同步运动工况Table 3 The asynchronous motion of the single-lifting mechanism
如图9a所示:随着位移变化量的增大,机位A承担的荷载增加,机位C、D承担的荷载值略有提高;当机位位移变化量达到36 mm时,机位B失载,此时机位A承担的荷载由30 kN增加到52.93 kN左右,提高了75%左右。如图9b所示:随着位移变化量逐渐增大到39.91 mm,机位B承担的荷载从40 kN增加至额定荷载80 kN,提升了1倍左右,机位C、D承担的荷载值略有下降。故端部机位超升或滞后会造成相邻机位失载或超载而后停机。

a—工况1; b—工况2; c—工况3; d—工况4。—A机位; —B机位; —C机位; —D机位。图9 单机位不同步工况Fig.9 The asynchronous motion of the single-lifting mechanism
如图9c所示,当机位位移变化20 mm时,机位B承担的荷载从30 kN增长至60 kN左右;当位移差值达到29.46 mm时,机位B超载。A、C机位承担的荷载逐渐减少,D机位承担的荷载几乎保持不变。如图9d所示:当机位位移变化30 mm时,机位A、C承担的荷载从30 kN增长至60 kN左右;而当机位位移差值达到21.11 mm以上时,机位B失载。故跨中机位的不同步升降,会造成机位本身发生失载或超载现象。
以上说明,当单个机位出现不同步运动的情况时,跨中机位受到的影响总是大于端部机位。同时,跨中机位往往要承担相邻机位的荷载,导致超载引起架体故障或过早失载而导致自身机位停机。
3.2 双机位不同步升降工况
表4列出了双机位不同步运动工况的基本方式,共计16个工况,其中包含相邻机位不同步运动、相隔机位不同步运动、端部机位不同步运动以及跨中机位不同步运动。

表4 双机位不同步运动工况Table 4 The asynchronous motion of the double-lifting mechanisms
在工况5的模拟试验中,固定C、D机位,同时给予机位A、B向上的位移。在工况6的模拟试验中,固定C、D机位,给予机位A向上的位移,给予机位B向下的位移。使两者的实时位移变化是相同的,直至两者的位移变化量都达到40 mm。同理,设计工况7~20的模拟试验。
由图10可知:在工况5中,当机位位移变化量达到44.66 mm时,机位C失载;在工况6中,当机位位移变化量达到23.03 mm时,机位B失载;在工况7中,机位B相对于A超升30.80 mm时,机位B达到75 kN额定荷载;在工况8中,当机位位移差值达到73.83 mm时,机位D承担的荷载逐渐减少至失载。

a—工况5; b—工况6; c—工况7; d—工况8。—A机位; —B机位; —C机位; —D机位。图10 端部相邻机位不同步工况Fig.10 The asynchronous motion of the adjacent-lifting mechanisms at the end
通过对比图9和图10可知:端部相邻机位发生不同步运动情况时,各机位荷载的增加和减少的幅度没有单机位不同步升降工况显著,但出现超载和失载时的位移差值比单机位升降时更大。故单机位不同步运动工况相较于相邻双机位不同步工况更为不利,容易引发事故危险。
由图11可知:在工况9中,当机位位移差值达到21.23 mm,机位B达到额定荷载,同时,若继续增大位移差值,四机位将相继发生超载或失载的现象,在施工中较为不利;在工况10中,当机位位移差值达到24.36 mm以上时,机位C失载,当跨中机位C承担荷载减小时,端部机位D承担的荷载要比相邻跨中机位B承担的荷载更多;在工况12中,机位位移差达到20.01 mm时,机位C失载。结合工况9可知,相隔机位同时发生同向运动时,跨中机位往往比端部机位响应更加剧烈。

a—工况9; b—工况10; c—工况11; d—工况12。—A机位; —B机位; —C机位; —D机位。图11 相隔机位不同步工况Fig.11 The asynchronous motion of the separated-lifting mechanisms
如图12所示:在工况13中,当机位位移变化量达到23.09 mm时,提升点C荷载减少至0 kN,机位A、B、D对应的超载或失载的位移差值为56.62,51.64,38.80 mm,说明初始荷载较小的机位对不同步运动反应程度更明显;在工况14中,当机位位移变化量达到48.46 mm时,机位C达到75 kN额定荷载后超载;在工况16中,随着位移变化量的增加,机位B、C承担机位A、D的荷载而迅速上升,其中,机位C承担荷载量明显大于机位B,机位D减小幅度明显大于机位A,当不同步差值达到18.90 mm时,D机位失载。
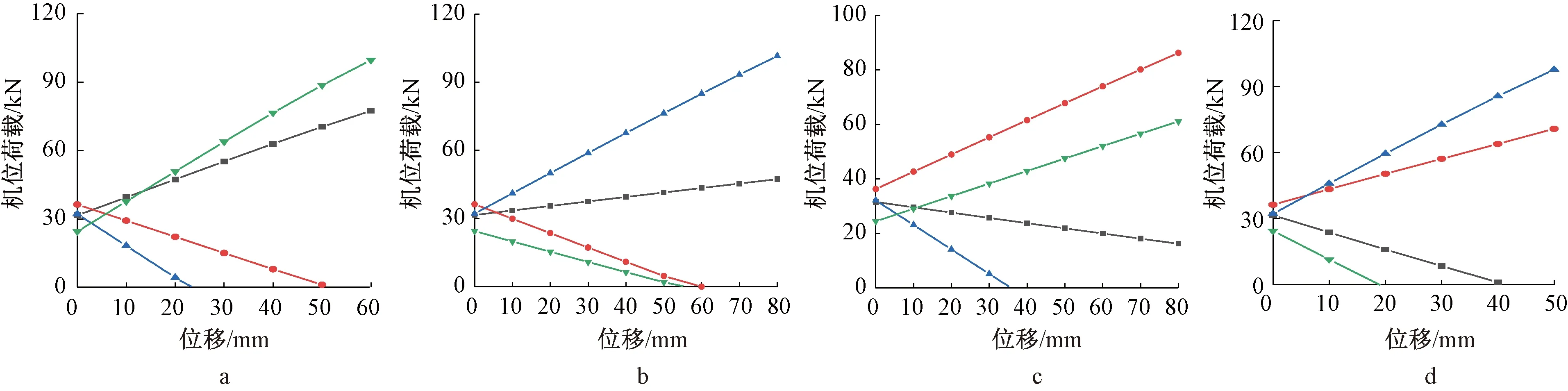
a—工况13; b—工况14; c—工况15; d—工况16。—A机位; —B机位; —C机位; —D机位。图12 双端部机位不同步工况Fig.12 The asynchronous motion of the double-lifting mechanisms at the both ends
如图13所示:在工况17中,当机位位移差值达到18.90 mm时,提升点C失载;在工况18中,当机位位移变化量达到19.85 mm时,机位C失载;在工况19中,机位B、C相继发生失载和超载,所对应的位移差值为20.327 mm和20.393 mm,证明不同步响应受到初始机位荷载的影响较大;在工况20中,当机位位移变化量在46.16 mm时,机位C出现失载,图中斜率可明显观察出初始机位荷载对不同步运动响应的影响程度。

a—工况17; b—工况18; c—工况19; d—工况20。—A机位; —B机位; —C机位; —D机位。图13 跨中双机位不同步工况Fig.13 The asynchronous motion of the double-lifting mechanisms at the center
通过对双机位不同步运动的16个工况进行分析,可以明显发现:单机位运动时荷载增减关系单一,双机位运动时需要考虑初始机位荷载对不同步响应的影响:初始机位荷载越小,对应的机位对架体不同步运动响应越明显,机位荷载变化量越大,也更容易发生超载或失载的现象。同时,由于双机位不同步运动在实际升降过程中最多且工况更加复杂,故也会出现端部机位失载导致架体故障的情况。
3.3 三机位不同步升降工况
三机位不同步运动在实际升降过程中也较为普遍,但是已有文献中没有对此类工况进行研究分析。本文结合试验统计,将三机位不同步运动情况分为如下两类,即A、B、C机位不同步运动和A、B、D机位不同步运动,共计12个工况,如表5所示。

表5 三机位不同步运动工况Table 5 The asynchronous motion of the triple-lifting mechanisms
由图14可知:在工况21中,当机位位移差值达到15.88 mm时,机位B失载。在相同位移变化量下,初始机位荷载相对较多的机位B的荷载变化量大于机位C;在工况22中,当机位位移差值达到42.56 mm时,机位B失载。端部固定机位荷载变化量大于端部超升机位,说明机位跨度对不同步响应存在影响,即机位跨度越小,则受不同步运动响应影响越明显;在工况23中,当机位位移差值达到19.76 mm时,机位C失载。其中,机位A承担的荷载出现下降的现象,说明提升和下降不是使得机位荷载变化的决定性因素,而初始机位荷载和机位跨度是影响不同步升降响应的主要因素;在工况24中,机位B、C因超升承担端部机位减少的荷载,端部机位最终失载;在工况25中,当机位位移变化量为14.43 mm时,机位C失载,机位B接近达到75 kN的额定限值;在工况26中,机位C超载时所对应的位移变化量为21.45 mm。同时,作为下降机位的A、B响应情况存在明显差别,机位B分担机位C传递的荷载量小于因自身滞后传出的荷载量,提升点B荷载减少,机位A滞后传出的荷载量小于提升点C传递的荷载量,故A机位荷载增加。由此可见,三机位不同步运动时,相同跨度下跨中机位对端部机位的影响要大于端部机位对跨中机位的影响。

a—工况21; b—工况22; c—工况23; d—工况24; e—工况25; f—工况26。—A机位; —B机位; —C机位; —D机位。图14 机位A、B、C不同步工况Fig.14 The asynchronous motion of the lifting mechanisms A, B and C
机位A、B、D不同步工况时应对机位C进行固定。由图15a可知:在工况27中,机位A承担自身荷载及机位B滞后而传递来的荷载,故增幅最大;机位C在接受机位B滞后而传递来的荷载时,并将荷载传出至超前机位D,由于B、D位移变化量相同,产生差异是机位布置位置、初始机位荷载以及距机位C的跨度。由此可见,因机位布置位置产生的不同步运动响应中机位A大于机位B、D。
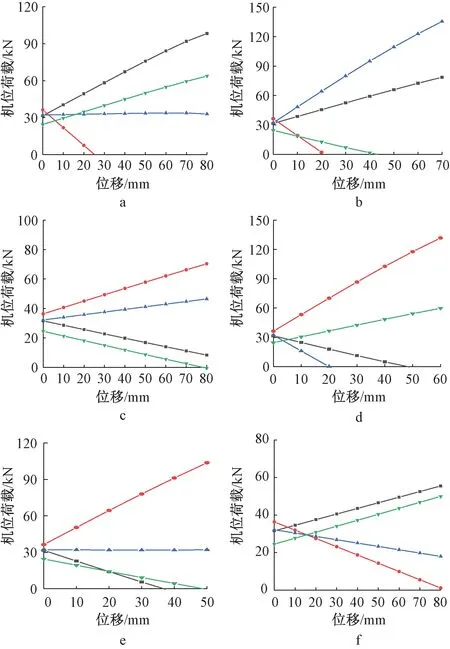
a—工况27; b—工况28; c—工况29; d—工况30; e—工况31; f—工况32。—A机位; —B机位; —C机位; —D机位。图15 机位A、B、D不同步工况Fig.15 The asynchronous motion of the lifting mechanisms A, B and D
由图15b、c可知:在工况28中,当机位位移变化量达到12.23 mm,提升点B荷载减少至0 kN,提升点C相继超载;工况29表现为跨中机位荷载迅速上升,端部机位荷载迅速下降。其中,机位B提升程度更多,故机位A相对滞后。
由图15d~f可知:在工况30中,当机位位移变化量为19.57 mm时,机位C失载;在工况31中,机位A、D因滞后失载,机位B达到额定荷载而后超载,机位C受机位B、D影响荷载变化基本恒定,证明机位位置是影响不同步运动响应的主要因素,而初始机位荷载及机位跨度为次要因素;在工况32中,机位B荷载由机位A、C承担,机位D超升,承担自身及机位C荷载。
4 设计建议
JGJ 202—2010规定,当相邻机位位移差超过30 mm、机位超载和机位失载时,均需停机调整或检查。为此,基于32种工况分析结果,统计了相邻机位位移差超过30 mm、机位超载和机位失载任何一种工况发生时机位的不同步系数,其最大值为2.33,最小值为1.16,平均值为1.82。目前JGJ 202—2010中规定的荷载不均匀系数为2.0,基于本文的分析,建议提高荷载不均匀系数至2.35或者降低允许的机位位移差,以保证升降脚手架的安全使用。
5 结束语
对全钢型集成式附着升降脚手架进行不同步运动性能试验研究,并建立有限元模型进行参数化分析,对单机位不同步运动工况、双机位不同步运动工况、三机位不同步运动工况下各机位承载性能的影响进行了研究,得到以下结论:
1)根据荷载传递路径,在试验中测得不同步运动过程中各测点的应力时程曲线。采用ABAQUS进行有限元分析,得到应力-位移曲线并与试验结果进行对比,各工况中测点的应力变化量误差在20%以内,证明采用有限元能够较为合理地反映实际升降不同步响应结果。
2)对有限元模型进行参数化研究,分析32个工况对于机位的承载性能的影响。研究表明:当单机位不同步运动时,中间机位受到的影响总是大于端部机位;当双机位不同步运动时,初始机位荷载越小,对应的机位响应越明显,机位荷载变化量越大,更容易发生超载或失载的现象;三机位不同步运动,证明了机位位置是影响不同步运动响应的主要因素,初始机位荷载和机位跨度为次要因素。
3)相邻机位位移差超过30 mm、机位超载和机位失载任何一种工况发生时机位的不同步系数,其最大值为2.33,最小值为1.16,平均值为1.82。目前JGJ 202—2010中规定的荷载不均匀系数为2.0,基于本文的分析,建议提高荷载不均匀系数至2.35或者降低允许的机位位移差,以保证升降脚手架的安全使用。
论文得到了天津大学刘红波教授的指导,天津大学硕士生于磊协助完成了试验,在此表示衷心的感谢。
