进口效应对小孔节流静压空气轴承静特性的影响
2010-07-25龙威,包钢
龙 威,包 钢
(哈尔滨工业大学 机电学院,哈尔滨 150001)
1 概述
空气轴承以其高精度、低摩擦和无污染的特点广泛应用于精密加工、医药卫生和航空航天等领域[1]。小孔节流空气静压止推轴承是一种常见的起支承作用的轴承结构形式。图1所示为典型的简单孔节流器[2],这种结构通常是指在直径为d的进气孔与轴承气膜交界处加工一个直径为d1和深度为δ的气腔凹穴。传统的轴承设计理论认为,当供气孔结构满足d<4h时,工作气体以等熵状态经过供气小孔,然后按照完全发展的层流形式以等温状态流经轴承间隙气膜,直至轴承边缘气膜间隙出口与外界大气环境相连通。然而Carfagno S P在试验中发现:试验压力曲线和通常经过层流假设的轴承径向压力分布曲线在气体流出供气孔和进入压力气膜之间的区域会出现压力骤降现象。在1966年,他首次提出在计算小孔供气静压止推轴承静态承载力时存在供气孔处的进口效应[3]。但其研究只局限在外径7.112 mm(2.8英寸)、供气孔直径0.050 8 mm(0.02英寸)的圆盘静压止推轴承在气膜厚度较大时的结果,没能将影响进口效应的具体因素做出详细分析。现代润滑理论结合空气轴承设计原理认为,这部分差异主要在于节流孔通过气腔向气膜过渡区间,流体因为流道形状的改变和流体间摩擦的加剧等原因,从完全发展的层流向紊流状态变化,目前尚没有准确的数学模型可以对其进行描述,只有通过完整描述轴承表面的压力分布对进口效应加以认识和描述。这使得对轴承表面、支承台面以及节流器的加工情况都要求极为严格,任何一点加工误差、表面误差或者外界环境的干扰都可能对试验结果产生重大的影响。文中从润滑气体的基本方程出发,推导小孔节流空气静压轴承间隙气膜内压力分布规律;在得到空气轴承静特性数学模型的基础上,分析造成和影响轴承进口效应的可能因素。通过参数优化,充分利用可能出现的多次节流效果提高空气静压轴承的承载能力,尽量减少进口效应可能产生的不利影响。
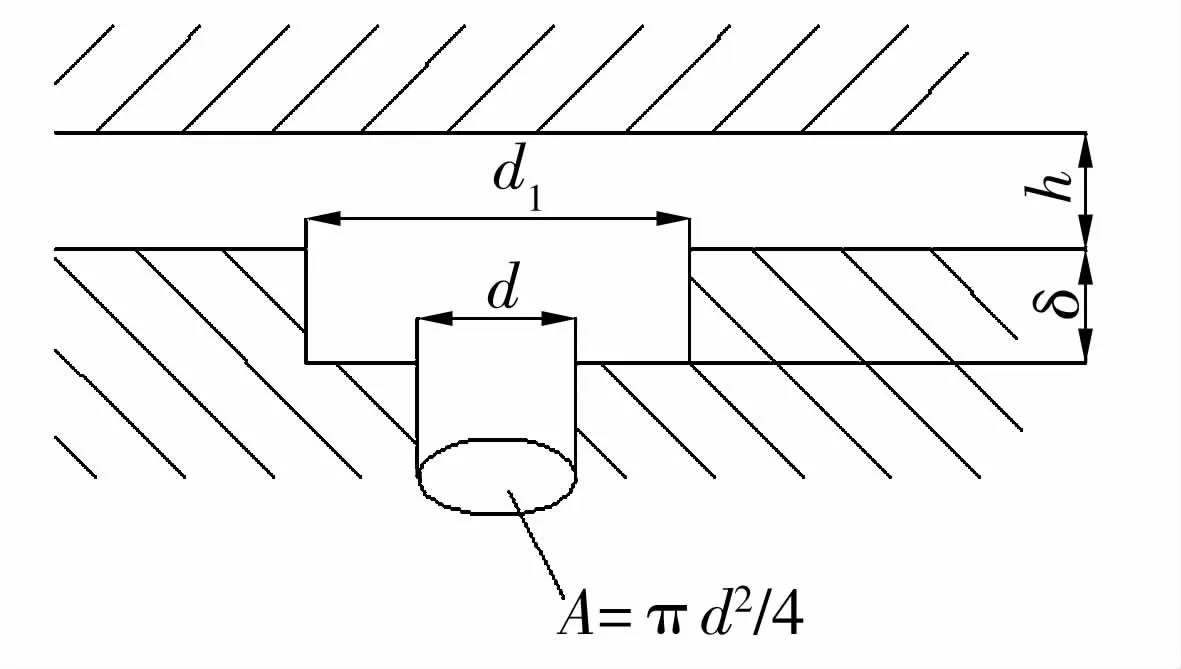
图1 简单孔节流器
2 数学模型的建立
在图2所示直角坐标系内建立外径为D,气膜厚度为h的中心供气小孔节流圆盘静压止推轴承结构示意图。其中进气小孔深度为l0,直径为d;在中心供气孔下方开一个高为δ,直径为d1的圆形气腔;外界气源供气压力为ps,气膜出口通环境大气压力为pa。定义:A11=πd2/4,A12=πd(h+δ),A21=πD21/4,A22=πD1h。由气体静压润滑理论可知:

图2 单孔静压止推轴承结构示意图
(1)当A22最小时,通过供气孔的气流直接从A22进入气膜,此时另外3个节流面都没有起作用,相当于只有一次环面节流,即:A22<min(A11,A12,A21),可将这种结构称为第1种节流形式,简称类型1。此时对轴承结构参数的具体要求为:
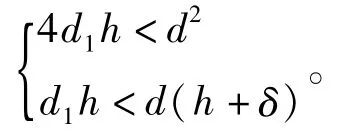
(2)因为d1>d2,所以A21恒大于A11,即A21不可能为最小。
(3)当A12最小时,则气流经供气孔从A12直接进入气腔,此处发生第1次节流,且节流类型为环面节流。当A22为次小时,气流流经气腔后从A22进入气膜,此处发生第2次节流,且节流类型为环面节流,即A12<A22<A11<A21。可将这种结构称为第2种节流形式,简称类型2。此时对轴承参数的具体要求为:
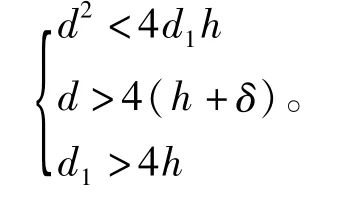
(4)当A11为最小时,则气流经供气孔后由A11离开供气孔,此处发生第1次节流,且节流类型为小孔节流。
当A12次小时,气流从A12进入气腔,此处发生第2次节流,其为环面节流。当A22为第3小时,气流从A22离开气腔进入气膜,此处发生第3次节流,其为环面节流,即A11<A12<A22<A21。可将这种结构称为第3种节流形式,简称类型3。此时对轴承参数的具体要求为:
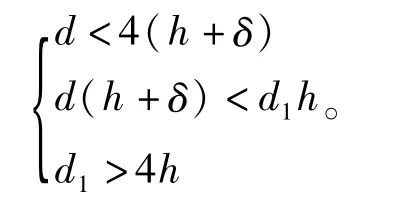
当A21次小时,气流从A21进入气膜,此处发生第2次节流,其为小孔节流,即A11<A21<min(A22,A21)。可将这种结构称为第4种节流形式,简称类型4。此时对轴承参数的具体要求为:
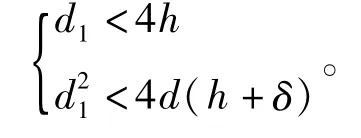
当A22次小时,气流从A11进入气腔,自A22离开气囊而进入气膜,此处发生第2次节流,其为环面节流,即A11<A22<min(A21,A12)。可把这种结构称为第5种节流形式,简称类型5。此时对轴承参数的具体要求为:
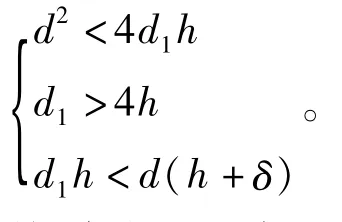
特别需要注意的是,很多假设情况下要求d1<4h,此时在小气膜厚度下工作时就使得d1必须很小才能满足假设条件,进而要求供气孔直径d更小,这不仅加工很困难,而且进气量也很小,即使在节流形式上满足了假设条件,仍无法得到较大的承载能力。设每经过一次节流作用后气体压力分别为pdi(i=1,2,3)。由文献[4]可知,轴承完整气膜内的Reynolds方程的一般形式可以写为:
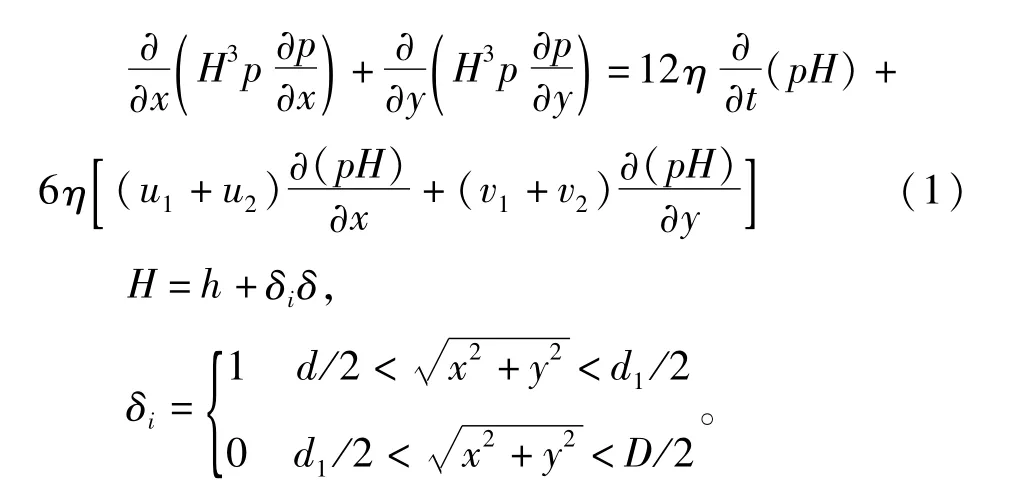
式中:H为广义气膜厚度;n为气体黏度;u1,u2,v3,v4为轴承的两侧面在x,y方向的运动速度。
(1)式与文献[3]气体润滑问题中均匀气膜的Reynolds方程在形式上具有一致性,但由于2次节流的效果,使得H在x-y上是间断的,这直接改变了气膜内压力分布规律,并对轴承的承载能力和刚度都有重大影响。由连续性原理进一步得到pd1,pd2,则气膜内的压力分布可由下式求得:

式中:wini为工作气体每经过一次节流作用时通过该节流面的气体流量。
3 模型实例分析
以环状均布6供气孔轴承为例,按前述分类,固定供气小孔固定流阻和供气压力ps,分析气腔直径和深度对轴承静承载能力的影响。选取轴承其他外形结构参数及供气参数见表1,5种节流类型下进气孔和气腔结构参数的取值范围见表2。
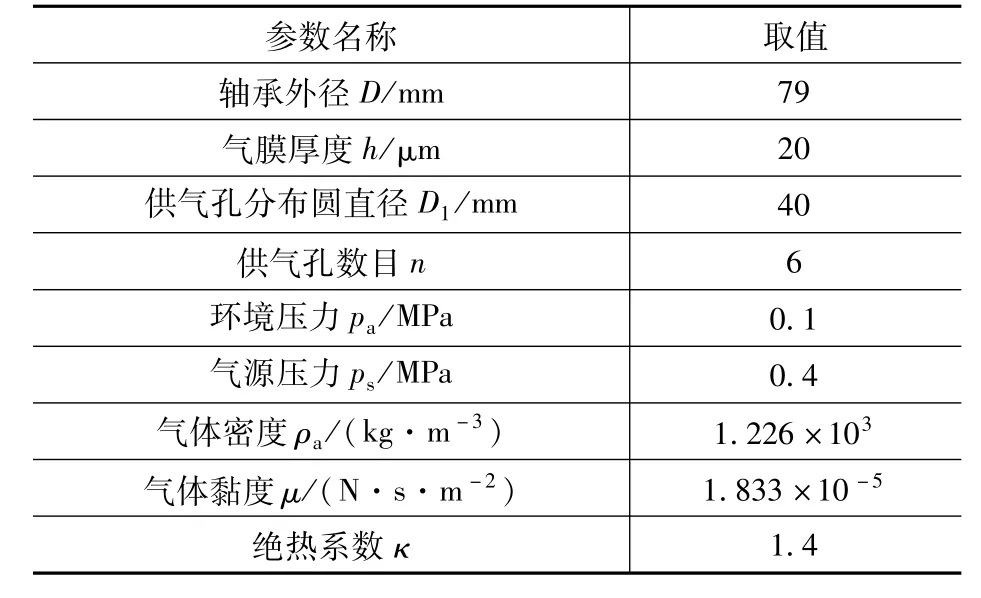
表1 轴承外形结构参数及供气参数
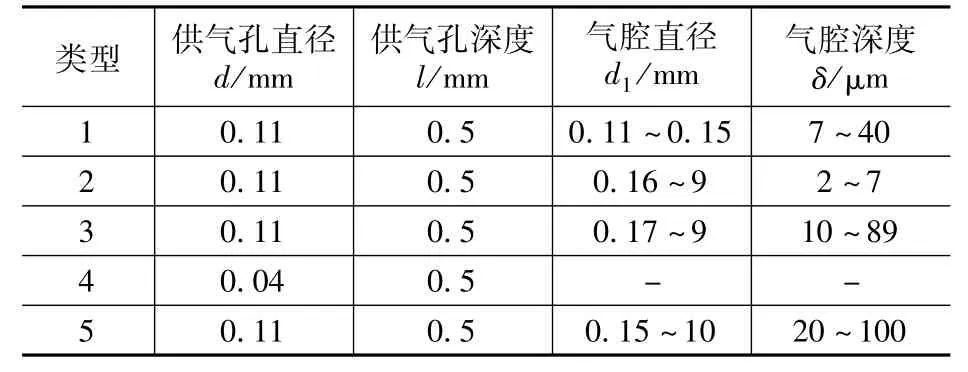
表2 不同节流类型时轴承节流器结构参数取值范围
按上述分类分析不同节流类型中气腔直径d1和气腔深度δ对轴承气膜内压力分布、轴承承载力、静刚度和耗气量的影响。固定供气压力ps=0.4 MPa,选择气膜厚度h=20μm,各节流类型下轴承节流器处结构参数取值范围如表2所示,其他结构参数及供气参数如表3所示。
由于类型4要求d1<0.08 mm,物理上又必须满足d1>d,该精度的供气孔在工艺上很难实现,而且对气体清洁度及过滤设备等要求也极为苛刻,因此尚不能应用于现实中,故忽略此节流类型。为标识明显起见,另外4种节流类型仍依次按类型1,类型2,类型3和类型5命名。
有限体积法[5]得出的离散方程要求因变量的积分守恒对任意一组控制体积都得到满足,对整个计算区域也自然得到满足;相比有限元法,有限体积法对网格质量要求低,得到的计算结果更为准确。其基本思路为:首先将完整的轴承气膜区域(含进气孔、气腔和气膜3部分)作为计算区域划分一系列不重复的控制体积,并使每个网格点周围有一个控制体积;将(1)式得到的偏微分方程对每个控制体积积分,得出一组相应的离散方程,其中的未知数是网格点上因变量的值;以进气孔入口压力和气膜出口压力作为边界条件,给出一组初始条件,假定值在网格点之间的变化规律;联立离散方程组求解,即可求出控制体积的积分。
4 试验装置
建立如图3所示试验装置[6],用来测量止推轴承气膜内的承载能力和静刚度。

图3 气浮轴承试验台原理图
试验台主体由施力杠杆、被试轴承及大理石支承平台组成。工作气膜间隙位于被试轴承和支承平台之间。气缸驱动施力杠杆,气膜间隙的高度通过施力杠杆在竖直方向的运动予以改变,具体数值由电感测微仪测出。试验轴承静承载力由应变式力传感器测得,为避免被试轴承在支承平面上发生平移或倾斜影响测试结果的准确性,通过定位板进行平面内的位置固定。在支承平台与被试轴承相对应的部分,沿轴承的半径方向确定多个测试点,可以测得工作气膜内沿半径方向的压力分布。在支承平台测压点处设置直径为0.2 mm的测压孔,小孔另一端出口外通压力传感器。在定位板的限制之下,改变被试轴承和支承平台之间的相对位置,测压孔可以位于不同的测试点,从而测得工作气膜内不同位置的压力值。为了保证试验结果的准确性,对于气膜内某一半径r处的压力值,可以令轴承在平面内固定位置沿垂直于支承平台的z向旋转一定角度,测得多个数值,求其算术平均值作为最终的测量结果,以消除单次测量可能带来的误差。
5 结果与讨论
图4分别给出4种节流类型中气腔深度对轴承承载力的影响:类型1中承载力先是随着气腔深度增加而增加,当气腔深度达到δ=30μm时承载力达到最大值,然后随着气腔深度的继续增加承载力略有下降;对于类型2,承载力随气腔深度变化近似呈线性增长,且气腔直径d1越小,线性化程度越高;对于类型3和类型5,承载力随气腔深度增加而迅速增长,达到最大值后基本保持稳定,且类型5增长的速度更为明显。
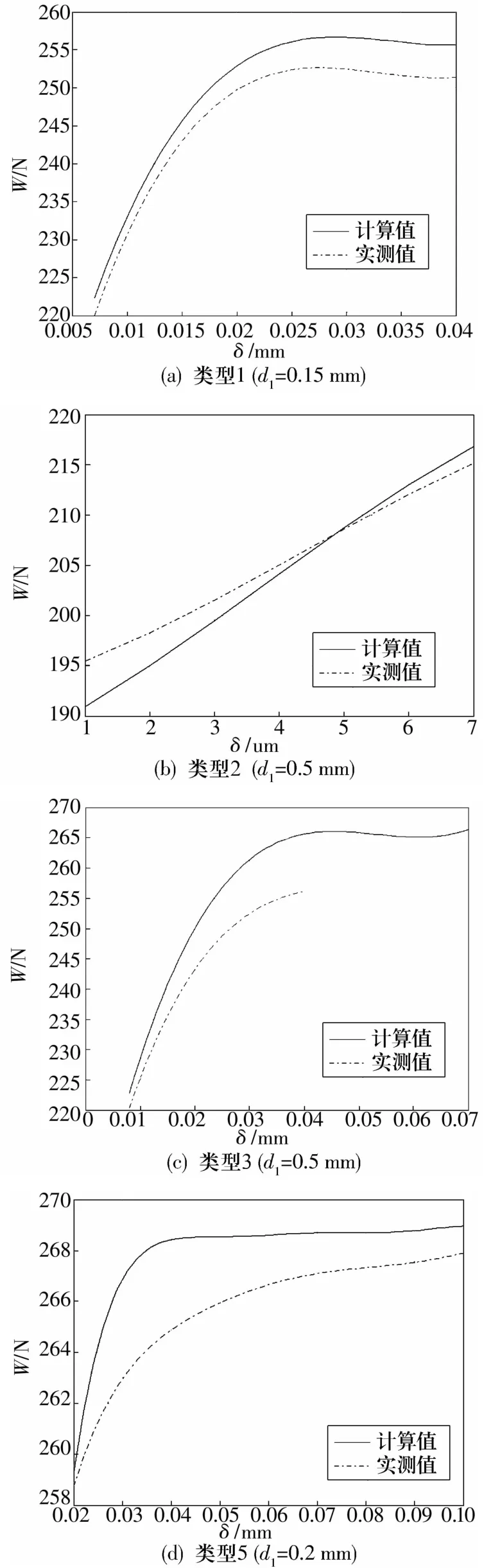
图4 气腔深度对轴承承载力的影响
图5分别给出4种节流类型中气腔直径对轴承承载力的影响:对于类型1,承载力随着气腔直径的增加而逐渐增大,当d1=0.126 mm时达到最大值,随后基本保持稳定,承载力变化ΔW/W=2.6%;类型2中承载力先是随着气腔直径的增加而增大,当d1达到5 mm左右时承载力达到最大值,然后随着气腔深度的继续增加而逐渐降低;对于类型3,承载力随气腔直径变化近似呈线性增长;对于类型4,在给定的气腔直径范围内,承载力随d1增长而增长,尤其在中间范围内增长的斜率较高,两侧的增长幅度较为缓慢。
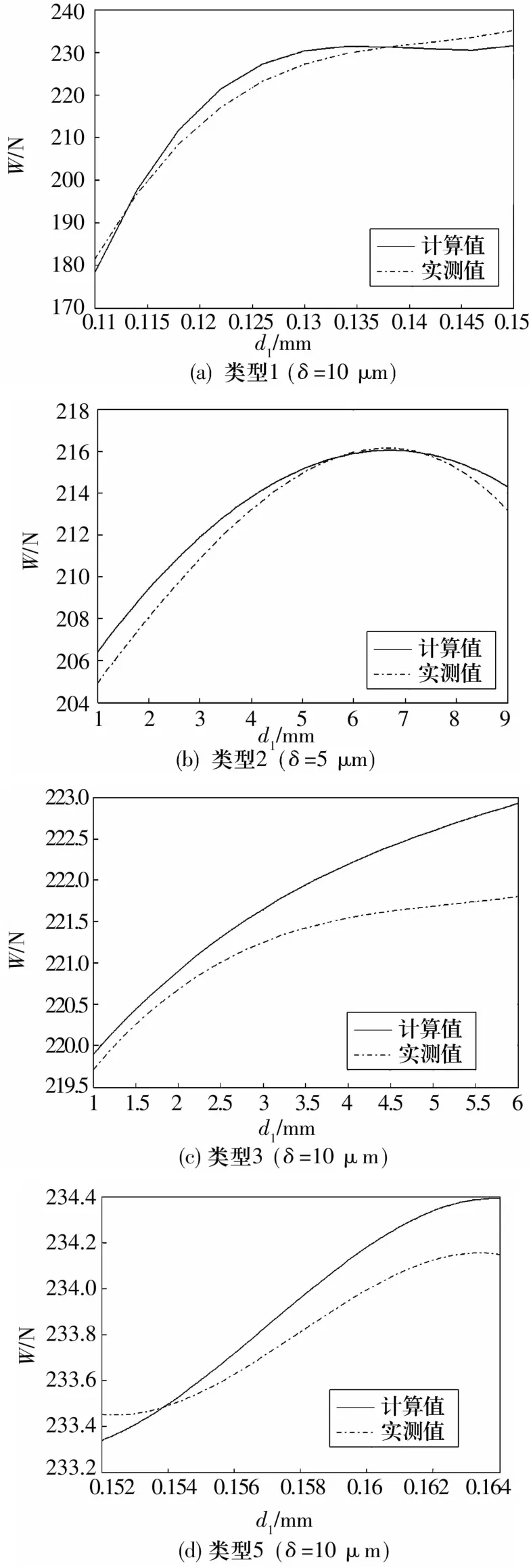
图5 气腔直径对轴承承载力的影响
将试验所得结果与计算仿真得出结果对比可知:随着气膜厚度增加,两者之间的吻合程度越高;随着气膜厚度减小,两者之间的偏差略为明显。这不仅是由于计算时采用的假设与实际过程之间存在差异造成的,也与现场试验条件、加工精度和仪器测量误差等有关。在试验允许的误差范围内,理论计算值与试验测得值基本符合,这证明了上文采用的理论分析方法合理有效,计算结果真实可靠,并为进一步研究空气静压轴承小孔节流的进口效应问题打下了重要的基础,使静压润滑理论在空气轴承设计方面得到了丰富和完善。表3为承载力最大时的轴承结构及静特性参数。
表3 承载力最大时的轴承结构及静特性参数
6 结束语
从二维定常Reynolds方程出发,建立小孔节流圆盘空气静压止推轴承的数学模型,根据节流效果不同将轴承分为4种节流类型,分别研究不同节流类型时结构参数造成的进口效应对轴承静特性的影响。使用有限体积法计算气腔深度和气腔直径对轴承承载力变化的影响规律,并给出承载力最大时气膜内压力分布规律。建立试验台,对结构参数对轴承承载力的影响规律进行了试验研究。介绍了试验台装置设计、工作原理和气膜内压力的测试方法。试验结果表明,文中对小孔节流进口效应的分析结论是正确的,计算结果合理可靠,具有满意的工程计算精度。
利用气腔进口效应构造多次节流的小孔式静压止推轴承对于制造精度有着严格的要求。在进行理论研究和优化设计的同时,制造工艺及零件检测技术也亟待提升,这也是制约我国自行开发高精度高承载能力支承试验台的一个主要因素。
