基于岭回归的4万亿经济刺激计划效果的评估
2010-07-23黎鹏
黎 鹏
(中南民族大学 经济学院,武汉 430074)
0 引言
为了应对金融海啸导致的全球经济危机,我国政府提出了4万亿经济刺激方案,力争我国经济增长“保八”。该方案能否确保“保八”目标的顺利实现,得到了海内外各界的关注,各种观点和预测层出不穷。根据凯恩斯的国民收入决定模型Y=I+C+G+EX,影响国民收入的四个因素为:投资I、消费C、政府财政支出G和出口EX。对照此模型,本文将影响经济增长的因素划分为4种,估计出在其共同作用下各个因素对经济增长的拉动作用系数。并根据系数评估4万亿经济刺激方案能否实现“保八”的目标。
1 模型构建与参数估计
1.1 对数线性模型简介
本文引入1个因变量序列:国内生产总值{GDPt},4个分别代表不同影响经济增长因素的自变量序列:全社会固定资产投资总额{It}、社会消费品零售总额{Ct}、国家财政支出{Gt}和出口额{EXt}。采用如下式(1)的对数线性模型来拟合。

之所以选择对数线性模型有如下两个理由:
(1)如下图1,自变量和因变量序列对时间呈现非线性的指数上升,对变量进行对数变换后可以有效剔除变量的非线性趋势;
(2)对于任意对数线性模型 Ln(Y)=β0+β1Ln(X)+ε 而言,方程两边同时对X求导,即可得整理得到所以对数线性模型的各个回归参数有明显的经济意义:体现了自变量变化率所导致的因变量变化率。具体对于本文模型式(1)而言,参数β1,β2,β3,β4分别表示自变量序列{It},{Ct},{Gt},{EXt}增长率所导致的因变量序列{GDPt}的增长率。
1.2 数据来源及初处理
选取1978~2008年的国内生产总值{GDPt}、全社会固定资产投资总额{It}、社会消费品零售总额{Ct}、国家财政支出{Gt}、出口额{EXt}和居民消费价格指数{GPIt}序列年度数据,长度为31年。其中1978~2007的30个年度数据来自于各年的 《中国统计年鉴》,由于2009的统计年鉴尚未最终出版,2008年的数据来自于国家统计局的相关统计公报。
考虑到历年通货膨胀率的影响,首先将自变量序列和所有因变量序列通过居民消费价格指数序列{CPIt}调整到以1978年价格水平计价的相对值,如图1。
对各个变量序列取自然对数剔除非线性指数趋势后,考虑到我们关心的仅是变量的变化率,而不是变量的绝对数值,所以将取对数后的以1978年价格水平计价的数据进行减去均值除以标准差的标准化处理。经过数据的初处理,最后进入回归的为以1978年价格水平计价对数化后标准化的数据。
由于经过标准化处理后的变量序列均转换成均值为0并且方差为1的序列,所以式(1)中的常数项参数β0变为0。式(1)退化为如下没有截距项的式(2):
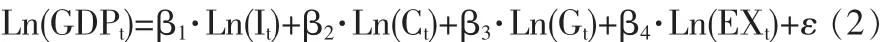
1.3 普通最小二乘法(OLS)的估计结果
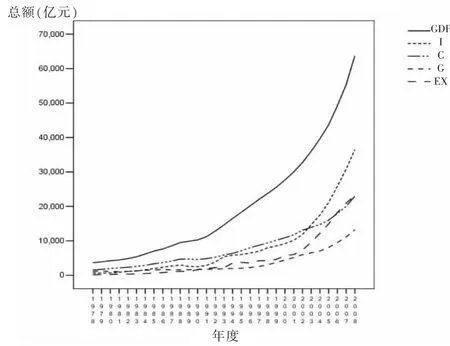
图1 以1978年价格水平计价的自变量与因变量序列图
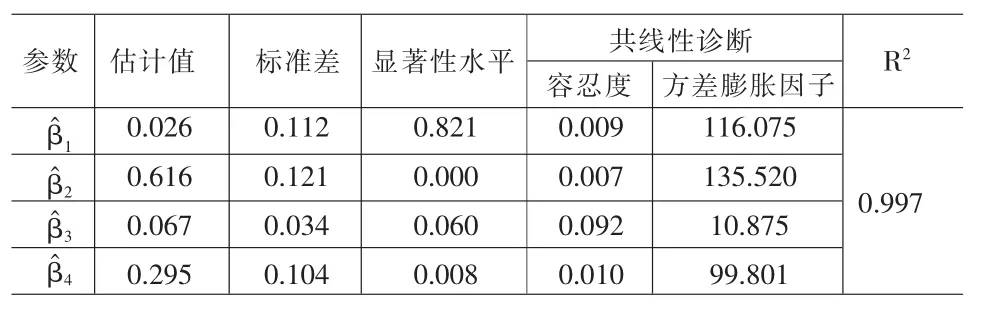
表1 普通最小二乘法估计结果表
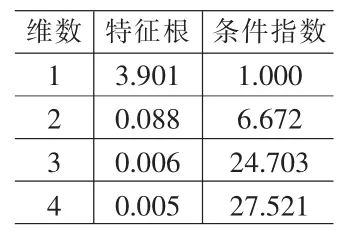
表2 特征根与条件指数表

表3 岭回归估计结果表(部分)
对经过初处理的数据采用普通最小二乘法估计式(2)模型得到结果如表1。
表1中,各个参数估计值符号正确,除β1外其他参数显著性水平较高;测定系数R2趋向于1,显示模型整体拟合效果较好。但是,各个参数的容忍度数值均小于经验值0.1,方差膨胀因子较大,并且表2中四个维数的特征根有3个趋向于0,四个维数的条件指数有两个趋向于30,均显示了该模型中自变量间的多重共线性较为严重。
多重共线性的存在通常会导致被估计参数方差过大、不稳定和不准确。具体到式(2)模型会导致无法相对准确的估计各个自变量增长率对因变量GDP增长率的弹性系数。为了有效克服模型自变量间的多重共线性问题,提高参数估计值的精度,必须采用其他估计办法。
1.4 岭回归(Ridge regression)的估计结果
对于任意回归模型Y=X·β+ε(其中Y为因变量观察值列向量,X为自变量观察值矩阵,β为被估计参数列向量,ε为误差列向量)而言,参数的普通最小二乘法估计为:

由于自变量间存在的多重共线性问题,导致方差协方差矩阵XT·X接近奇异矩阵即|XT·X|→0,进行矩阵求逆运算后(XT·X)-1内的各元素都很大, 从而导致被估计参数β的方差协方差均很大。
如上分析,在多重共线性的情况下,参数估计不准确的根本原因是矩阵XT·X趋向一个奇异矩阵。岭回归正是在矩阵XT·X上加上一个k倍的单位矩阵 I使得 XT·X+k·I不再近似为一奇异矩阵,从而克服多重共线性对参数估计的影响。参数估计值由式(3)变为如下式(4):

使用经过初处理对数化后标准化的数据得到式(2)的岭回归估计结果如图2、图3和表3。
观察图2岭迹图发现当k=0.8时,各参数估计值趋向与稳定,图3中显示测定系数R2始终保持在0.975以上,模型整体拟合效果较好,参数估计值符号正确。选定在k=0.8时得到的岭回归模型估计结果如下式(5):

图2 参数估计值的岭迹图
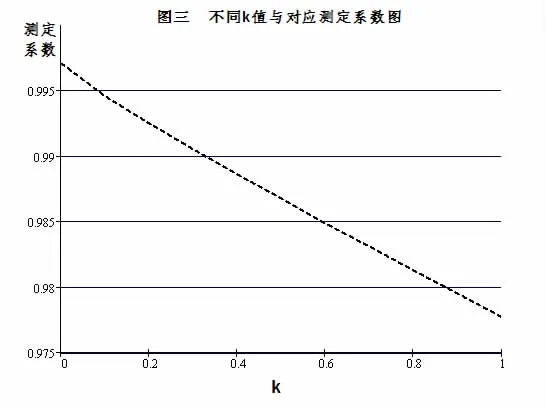
图3 不同k值与对应测定系数图

2 结论
依据模型估计结果式(5),得到如下结论:
(1)在拉动GDP增长的四个因素当中,每增长1个单位的投资I拉动GDP增长0.24,1个单位的消费C拉动增长0.338,1个单位的政府支出G拉动增长0.112,1个单位的出口EX拉动GDP增长0.309。不同因素增长相同1个单位对GDP增长的拉动作用大小取决于其对应参数β估计值的大小,依次为:消费C>出口EX>投资I>政府支出G。
在拉动经济增长的因素中,消费C的作用最大,政府支出G的作用最小。按照参数估计结果,逻辑上来说,两者相同的一个单位增长对于拉动经济增长来说,消费C的效果大概是政府支出G的3倍左右。直接刺激消费C显然比增加政府支出G对GDP增长的拉动作用更大。但是,消费C由每个微观经济个体决定,取决于个体的收入水平和对未来的预期,属于不可控或者不完全可控的因素;而财政支出G属于可控或者大部可控因素。政府只能选择财政支出G为作用变量。同样数额的财政支出G投入方向的不同,对消费C的影响亦不同。如:增加转移支付和减税等会对消费C有一定的刺激作用,增加基础设施等对消费C的刺激作用则较小。
(2)根据估算出的2009年各因素增长率可以测算出它们拉动GDP的增长率及在4种因素共同作用下最终的GDP增长率,结果如下表4:
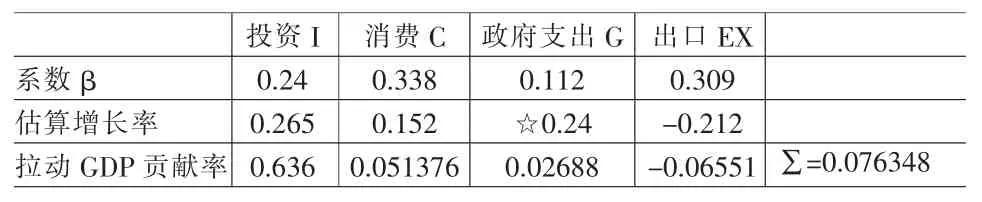
表4 各因素估算增长率及其对拉动GDP贡献率
表4中数据计算办法按照如下式(6)和式(7)进行

其中投资I、消费C和出口EX的估算增长率为2009年1-2月份实际统计数据,来自于国家统计局的相关统计公报;政府支出G增长率来自于《2009年政府预算报告》中的“中央财政支出43865亿元,增加8485.01亿元,增长24%”,同时假设地方财政支出的增幅不小于中央财政支出的增幅。
基于上述的结论,如果投资I、消费C和出口EX在未来10个月内维持1-2月份的增幅,并且政府财政支出切实落实的情况下,在考虑到计算误差后,2009年的GDP增幅可维持在8%左右。但是,实际情况也许更加困难一些。
正如温家宝总理所说,心暖则经济暖。要坚定信心,只有信心才能产生勇气和力量,只有勇气和力量才能战胜困难。面对当前的形势,只要应对得当,我国经济必将领先于世界其他经济体回暖。
[1]张海星.《中国FDI与国内投资经济增长效应的比较分析》[J].财经问题研究,2005(11).
[2]刘晓霞,周庄.基于协整分析的我国经济增长、消费和投资关系研究[J].现代经济,2007,6(5).
[3]郭健.税收、政府支出与中国经济增长的协整分析[J].财经问题研究,2006(11).
[4]康赞亮 张必松.FDI、国际贸易及我国经济增长的协整分析与VECM模型[J].国际贸易问题,2006,(2).
[5]高素英,李延军,金浩.岭回归在经济增长影响因素分析中的应用[J].统计与决策,2005,(5).
[6]田晖.基于岭回归法的居民消费行为影响因素实证分析[J].消费经济,2007,(6).
[7]张文彤.SPSS11统计分析教程[M].北京:北京希望电子出版社,2002.
[9]郝黎仁等.Mathcad 2001及概率统计应用[M].北京:中国水利水电出版社,2002.
