基于FPGA的并行FIR数字滤波器硬件实现及优化

2010-07-17郑维智江远志

食品科学技术学报 2010年5期

付正，郑维智，江远志

(北京工商大学机械工程学院，北京 100048)

现场可编程逻辑器件FPGA是可编程逻辑器件中一个重要的分支. FPGA使用了可编程领域中最常用的硬件描述语言VHDL，以及Max-plus Ⅱ作为仿真软件. FPGA在网络、数据处理、仪器、军事、工业控制、通信和航空航天等众多领域都得到了广泛应用，随着功耗和成本的进一步降低，FPGA还将进入更多的应用领域[1-2].

本文在一个有限脉冲响应数字滤波器(finite impulse response,即FIR)的可编程逻辑器件实现的基础上做了一定的优化和改进，详细地阐明了滤波器涉及的流程和原理.

1 有限脉冲响应数字滤波器FIR

所谓并行FIR滤波器指的是数据是并行输入的，对这些数据的处理也是并行的，这样能够达到在一个时钟内对一个输入数据进行处理的目的.

数字滤波器通常都是用来改变时域或频域中信号的属性的. 其中最为常见的数字滤波器是线性时不变(linear time-invariant,LTI)滤波器. 输入信号经过LTI滤波器时经过了一个称为线性卷积的过程. 用公式可以表示为y=f*x，其中f指的是滤波器的脉冲响应函数，x表示的是输入信号，而y则表示卷积输出. 线性卷积过程的定义如下：

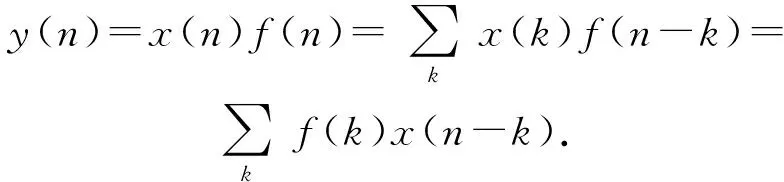
(1)

线性时不变数字滤波器分为无限脉冲响应滤波器(infinite impulse response,即IIR)和有限脉冲响应滤波器FIR两大类. 顾名思义，FIR滤波器是由有限个采样值组成的，只需进行有限次卷积，而IIR滤波器则要执行无限数量次卷积.

有限脉冲响应滤波器可由式(2)的差分方程表示

(2)

式(2)中，bl系数和系统的脉冲响应是直接相关的，bl=h(l). 因此式(2)可改为

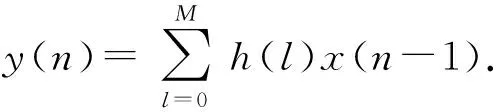
(3)

对式(3)进行Z变换，得到式(4)输入输出关系

(4)

在实际应用中，式(4)由几个不同形式的部件组成：延时器，乘法器，加法器.

带有常系数的FIR滤波器是一种LTI数字滤波器. L阶或者长度为L的FIR输出对应于输入时间序列x(n)的关系由一种有限卷积形式给出，具体的形式如下：

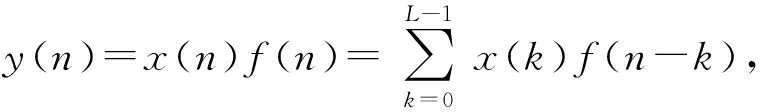
(5)

其中从f(0)≠0一直到f(L-1)≠0均是滤波器的L阶系数，同时也对应于FIR的脉冲响应. 对于LTI系统可以更方便地将上式表示成为z域内的形式：

Y(z)=F(z)X(z).

(6)

其中F(z)是FIR的传递函数，其z域内的形式：

(7)

2 并行FIR滤波器结构的优化

传统的线性FIR滤波器的实现结构如图1.

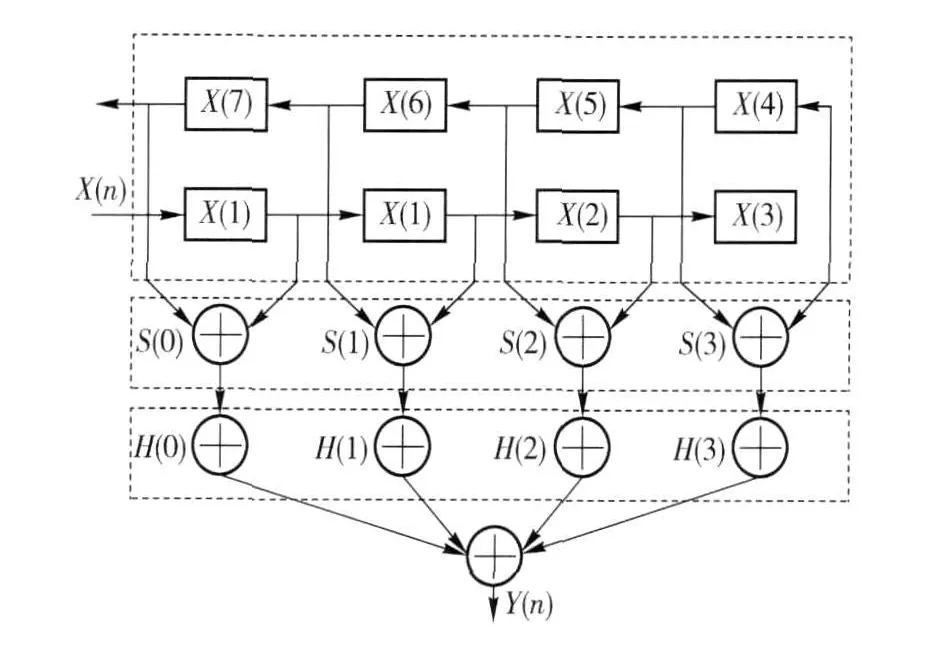
图1 传统的线性FIR滤波器的实现结构Fig.1 Traditional linear FIR filter implementation structure

对于改进型的结构主要在于并行矢量乘法器模块，由于它占用这个系统的大量资源，其设计决定了整个系统设计是否优良. 并行矢量乘法器模块的设计方法有许多种，见图1，输入数据与冲击响应相乘是通过乘法器完成的，然后利用加法器把它们相加起来. 这样设计存在比较大的缺陷，主要是乘法器的实现非常困难，会占用很多资源，系统冗余很大，因此需要的时钟延迟也比较长. 本文采用了查找表的方法来设计并行矢量加法器(见图2).

2.1 A/D模块

数字滤波器需要处理的是离散信号，因此必须先将输入的模拟信号通过模数转换成离散信号.

图2 并行FIR滤波器的模块划分Fig.2 Parallel FIR filter module division

2.2 并行时延模块

A/D模块的采样数据首先送到并行时延模块中，在每个时钟周期内都将下一组数据向下移动一位，由于器件中的逻辑单元均带有同步使能的可编程触发器，因此将移位寄存器组中的每个移位寄存器都设计成一组并联的D触发器，D触发器个数为输入数据的有效位数. 因为所有D触发器共用一个时钟脉冲，所以每个时种均可以输出一组数据，从而使每个移位寄存器实现了一个时钟延迟，完成需要的功能.

2.3 加法器组模块

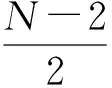
2.4 抽头系数模块

抽头系数模块是人工将抽头系数的所有可能的组合都固化在FPGA的ROM中. 通过加法器模块的作用输出数据相应位的组合，然后根据查找表输出相应的值.

2.5 移位相加模块

移位相加模块是通过对显示查找表(look-up-table，简称LUT)输出的值进行移位相加来实现乘法功能的，在经过了移位相加运算后，通过寄存器输出y(n)的值.

3 各模块具体功能的实现

为了使设计的实际效果更加直观，举例说明16阶线性FIR低通滤波器的具体实现过程.

假设输入为：x=sin(40πt)+0.2cos(400πt)，如图3，其中xb=0.2cos(400πt)是叠加在x=sin(40πt)的干扰信号. 叠加之后的输入信号波形如图4，设计指标为：ωp=0.1π，xs=0.15π，fs=1 000 Hz.

滤波器的频率响应波形如图5.

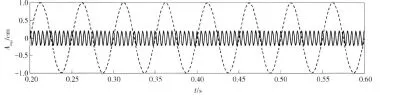
图3 源信号与干扰信号的波形Fig.3 Source signal and interference signal waveform

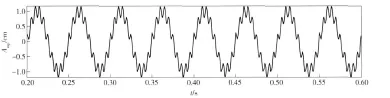
图4 叠加后输出波形Fig.4 Superposed output waveform

图5 滤波器的频率响应波形Fig.5 Filter frequency response waveform

3.1 输入信号的抽样和量化

输入信号的抽样和量化用于并行方式中的模数(A/D)转换，其目的就是通过对连续信号进行抽样并量化成二进制补码的形式将之变为数字信号，即x(n). EP1K30系列FPGA只支持定点运算，以此来实现更高的速度和更低廉的成本，因此必须对采样信号进行相应的转换，通常采样信号的数值比较小，需要先将之放大，之后把放大后的信号转换成7位二进制补码的形式. 值得注意的是，这个转换过程是通Mat1ab仿真来实现的[3].

3.2 预相加模块

预相加模块是由并行时延模块和加法器组模块组成的. 其目的主要实现在每个时钟周期将输入的采样数据x(n)进行延时，同时将对称的那些抽头系数中的x(n)预相加，最后将结果输出到抽头系数模块中. 在该模块中，x-in(6:0)是采样输入信号，clk代表系统时钟，sum0，suml，sum2，sum3是八阶滤波器预相加的结果并行输出信号.

具体程序如下:

Library ieee;

Use ieee.std-logic-1164.all;

Use ieee.std-logic-arith.all;

Use ieee.std-logic-unsigned.all;

Entity preadd is

Port(x-in : in std-logic-vector(6 downto 0);

Clk : in std-logic;

Sum0,sum1,sum2,sum3: out std-logic-vetor(7 downto 0);

End preadd;

Architecture Behavioral of Preadd is

Signal x0，x1，x2，x3，x4，x5，x6，x7:std-logie-vector(6 downto 0):=“0000000”;

Signal x0-temp，x1-temp，x2-temp，x3-temp，x4-temp，x5-temp,

X6-tem，x7-temp:std-logic-vector(7 downto 0);

Component reg

Port (d: in std-logic-vector (6 downto 0);

cIk: in std-logic:

q: out std-logic-vector(6 downto 0)

);

End component:

Begin

P1: reg port map(x-in，clk，x0);

P2: reg port map(x0,clk,x1);

p3: reg port map(xl，clk，x2);

p4: reg port map(x2，clk，x3);

p5: reg port map(x3，clk，x4);

p6: reg port map(x4，clk，x5);

p7: reg port map(x5，clk，x6);

p8: reg port map(x6，clk，x7);

xo-temp<=x0(6)&x0;

xl-temp<=x1(6)&x1;

x2-temp<=x2(6)&x2;

x3-temp<=x3(6)&x3;

x4-temp<=x4(6)&x4;

x5-temp<=x5(6)&x5;

x6-temp<=x6(6)&x6;

x7-temp<=x7(6)&x7;:

sum0<=x0-temp+x7-temp;

sum1<=x1-temp+x6-temp;

sum2<=x2-temp+x5-temp;

sum3<=x3-temp+x4-temp;

end behavioral

3.3 抽头系数h(n)的确定

将滤波器的截止频率设置为50 Hz，ωp=0.1π，借助于Matlab仿真软件通过调用相应的窗函数，通过截止频率和设计滤波器的阶数两个参数调用firl函数，求出滤波器的脉冲响应系数h(n).对应于不同的窗函数，所求得的h(n)见表1，通常用8位字长来表示h(n).

3.4 乘累加模块的实现

此模块又包括抽头系数和移位相加两个子模块. 作为FIR滤波器优化的主要方面，采用基于查找表结构的模数转换改进结构来替代传统的硬件乘法器. 由于使用的是四输入的LUT，因此为了节省硬件资源，将16阶滤波器变为两个级联的八阶FIR数字滤波器，这样有利于扩展成更高阶的滤波器. 由于h(n)具有对称结构，对于八阶线性FIR滤波器可以采用四输入的形式，将h(n)有可能出现的各种组合预先存在查找表中，参见表2.

表1 采用汉明窗得到的h(n)Tab.1 Obtained by Hamming window h(n)

表2 16阶FIR滤波器的LUT表(8位)Tab.2 16FIR filter LUT order form (8)

为了使设计更具有普遍性，在设计中所有的数据使用的都是二进制补码的形式，由于中间的计算过程可能会出现数据溢出，从而导致计算结果产生无法估量的错误. 因此在两个数据相加的时候采用增加符号扩展位的方法来防止数据溢出，实践证明这种方法十分有效. 具体做法：将要相加的两个数的最高位的符号位均向前扩展一位，这么做就保证了中间计算结果的正确性. LUT的输出位宽是9位,而其中最高位为符号扩展位. 因为输入数据位宽是8位，因此在并行结构中，sb(n)[b=0,1…7]分别对应了8个查找表，而前7位对应的查找表完全相同;对于最高位(符号位)对应的查找表，为了全部用加法器以提高运算速度，输入到该查找表的数据是表3的补码形式. 另一个级联的8阶滤波器设计方法与上述内容完全相同，唯一不同的是写入ROM中的数值为h(4)，h(5)，h(6)，h(7)的所有组合形式，得到的实验结果如图6. 本设计中LUT是由抽头系数模块来实现的，其实现方式通过EP1K系列器件中的Core generator和VHDL语言将以上数据固化在ROM中，这样做使模块的可移植性更好. 另外并行移位相加模块是将sum0，sum1,sum2,sum3中相同的有效位来组成地址信号，之后通过LUT输出值table-out[0:8]得到相对应的部分积，最后通过移位寄存器和加法器将上面得到的部分积相加，从而得到了最终的乘积y(n). 其模块符号如图7.

表3 16阶FIR滤波器的LUT表(9位)Tab.3 FIR order filter LUT table (9)

图6 经过滤波后的输出波形Fig.6 After filtered output waveform

图7 四乘8位乘累加模块符号Fig.7 4×8-bit multiply accumulate module symbols

4 并行FIR滤波器的流水线设计

在FPGA中通过流水线技术进行并行可重复配置高精度的FIR滤波器设计，方便地改变滤波器的系数和阶数. 采用这种FIR滤波器的设计方法可以充分发挥FPGA的优势.

FIR滤波器中的流水线技术不仅可以扩展信号频带和滤除多余的噪声，还可以通过改变信号的特定频谱分量来得到预期的结果. 数字滤波器在无线通信等领域中有着广泛的应用. 在数字信号处理中，传统滤波器是通过高速乘法累加器来实现的，这种方法的缺陷在于，在下一个采样周期到来前滤波器只能进行有限操作，因此带宽受到了限制. 通过使用并行流水线结构的FIR滤波器，可以使即便64阶、128阶甚至更高阶的滤波器与16阶滤波器的速度一样快，其特点是在算法的每一个阶段存取数据. FPGA结构使得在以采样速率处理数字信号的过程中，常数乘法器成为理想的载体，从而提高了整个系统的速度和效率. 值得注意的是，由于设计要求存在差异，在整个设计过程中，各个环节也会有所不同，这就需要根据不同的要求对数据进行不同的处理，如截断、扩展等，最终才能设计出既满足设计需要，又节省FPGA资源的电路.