条件推测性十进制加法器的优化设计
2016-10-13崔晓平王书敏刘伟强董文雯
崔晓平 王书敏 刘伟强 董文雯
条件推测性十进制加法器的优化设计
崔晓平*王书敏 刘伟强 董文雯
(南京航空航天大学电子信息工程学院 南京 210016)
随着商业计算和金融分析等高精度计算应用领域的高速发展,提供硬件支持十进制算术运算变得越来越重要,新的IEEE 754-2008浮点运算标准也添加了十进制算术运算规范。该文采用目前最佳的条件推测性算法设计十进制加法电路,给出了基于并行前缀/进位选择结构的条件推测性十进制加法器的设计过程,并通过并行前缀单元对十进制进位选择加法器进行优化设计。采用Verilog HDL对32 bit, 64 bit和128 bit十进制加法器进行描述并在ModelSim平台上进行了仿真验证,在Nangate Open Cell 45nm标准工艺库下,通过Synopsys公司综合工具Design Compiler进行了综合。与现有的条件推测性十进制加法器相比较,综合结果显示该文所提出的十进制加法器可以提升12.3%的速度性能。
十进制加法;条件推测十进制加法;并行前缀;进位选择加法器
1 引言
提供硬件支持十进制浮点(Decimal Floating Point, DFP)算术运算正在成为一个热门的研究方向,2008年发行的IEEE 754标准的修订版本(IEEE 754-2008)[1]包括DFP算术运算的最新规范。越来越多的处理器制造商倾向于在自己的处理器芯片中集成专用的十进制浮点运算单元,IBM面向工作站和服务器的Power 6[2]微处理器以及Z10大型机[3]的处理器中已经包括了完全符合IEEE754-2008标准的十进制浮点运算硬件单元。在处理器中提供专用的十进制运算单元将成为趋势。
十进制算术运算中最基础的十进制加法一直是研究的热点,目前的十进制加法运算基本上采用8421二-十进制编码(Binary Coded Decimal, BCD),采用8421-BCD码设计十进制加法器的优势在于可以利用二进制加法器中成熟且性能优越的电路结构来设计十进制加法器,使其电路结构更为简单与规整。不论在二进制加法还是十进制加法中,影响加法电路运算速度的主要因素在于低位向高位传播的进位链。二进制加法和BCD 十进制加法的不同点是:(1)二进制加法的进位规则是逢二进一,其进位的产生与传递比较简单,而十进制加法运算需要计算十进制数之间的进位,其进位规则是逢十进一。(2)4 bit编码的8421-BCD共有16种状态,其中6种编码(1010,1011,1100,1101,1110, 1111)是误码,因此,当采用二进制运算方法对4 bit 8421-BCD进行相加运算时,需要对二进制运算结果进行修正。
为了提高8421-BCD码十进制加法的性能,研究人员提出了多种算法与结构,其中最经典的两种方法是直接十进制加法[5]和推测性十进制加法[7]。直接十进制加法是一种无需进行修正的十进制加法算法,该算法推导出直接产生十进制和与十进制进位的方法,在IBM S/360 Model 195机型的处理器中使用该算法完成浮点运算[4]。推测性十进制加法采用预先修正,二进制求和并再修正的算法,这种采用预先修正的十进制加法,称之为推测性十进制加法。文献[7-9]根据此思路提出了条件推测性十进制加法,即有条件地对操作数进行预先加6修正。
条件推测性十进制加法器主要包括+6预处理模块、二进制并行前缀加法器模块和十进制进位选择加法器模块。二进制并行前缀加法器(Parallel Prefix Adder, PPA)可以看成是超前进位加法器的一种改进结构,其常见的结构包括Kogge-Stone(KS)树[18]、Brent-Kung(BK)树[14]、Sklansky(SK)树[15]、Han-Carlson(HC)树[16]等基本树形结构和并行前缀/进位选择混合加法器(Hybrid Parallel-Prefix/ Carry-Select Adder, PPF/CSA)结构。并行前缀/进位选择混合加法器被广泛应用于宽位加法器的设计中。
文献[7-9]使用QT (Quaternary Tree, QT)树形结构[12]产生进位信号,该结构与基于SK的PPF/ CSL加法器结构相同,进位选择加法器模块的长度为4,适用于设计4位一组的BCD十进制加法器。SK树形结构随着操作数位数的增大,其最大扇出数呈线性增长,导致延迟时间增大。KS并行前缀加法器具有最短的延时,且结构规整并具有相同的扇出因子,但不足之处是复杂度随着操作数位数增加,因此导致面积和功耗的增大,采用基于KS的PPF/CSA加法器结构可以得到高速的十进制加法器。本文重点研究基于KS的PPF/CSL十进制定点加法器的算法与相关结构,并在第3节针对条件推测性十进制加法器给出优化设计方法以降低电路的复杂度。
本文结构如下:第2节介绍了基于8421-BCD码的十进制加法;第3节给出了新的基于KS结构的条件推测性十进制加法器的设计;第4节给出了仿真结果并与现有的二进制和十进制加法器进行了对比分析。
2 基于8421-BCD码的十进制加法概述
在设计bit(=4)十进制加法器时,采用8421-BCD码对两个位宽为的十进制被加数和加数进行编码,具体形式为
基于8421-BCD码的十进制加法的基本算法是:首先对十进制被加数和加数按二进制加法进行运算,再对运算结果进行纠错。产生错误的原因是十进制数相加的进位原则是“逢十进一”,而4 bit二进制数相加采用“逢十六进一”的进位原则,两者相差6。因此,按二进制数运算规则得到的8421-BCD码运算结果需要修正。修正的方法是当和数大于9或产生进位时,需要对该位的和加6修正。上述算法的最大缺陷是修正时的进位链会导致延时增加。研究人员提出了几种改进方法,主要有直接十进制加法[5],推测性十进制加法以及条件推测性加法。
1位直接十进制加法的输入为8421-BCD码的十进制被加数,加数以及一个1 bit的十进制进位输入信号,直接产生十进制和,以及一个1 bit的十进制进位输出,的位权是的10倍,其表达式为
推测性十进制加法对操作数的每一个十进制位先加6,然后对按照二进制的方法进行求和,如果该十进制位的进位输出为0,则说明加6操作是多余的,进行减6修正,其结构如图1所示。
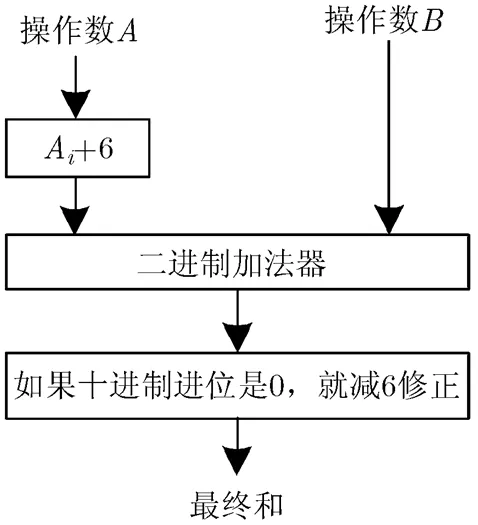
图1 推测性十进制加法结构图
文献[7-9]依据此思路提出有条件的推测性加法算法,该算法没有对操作数的所有十进制位A加6,而是根据一定条件判断是否需要对某个十进制位进行加6预操作,称之为条件推测性十进制加法,条件推测性十进制加法结构如图2所示。
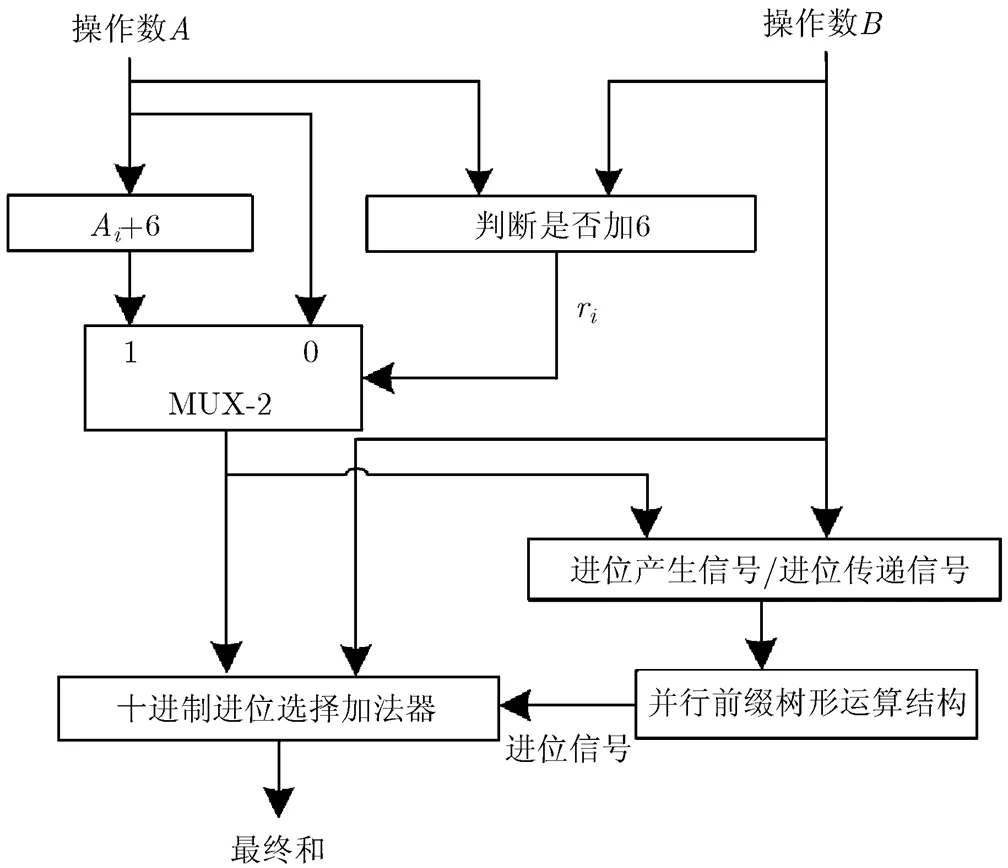
图2 条件推测性十进制加法结构图
由此可以得到:
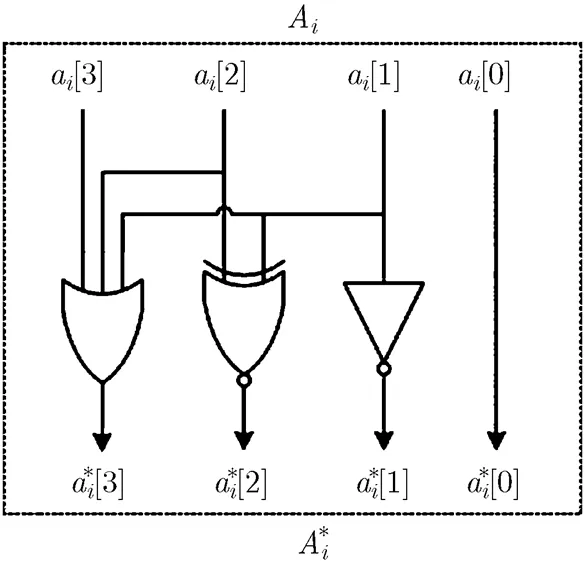
图3 加6操作电路图
3 建议的基于KS结构的条件推测性十进制加法器的设计
在设计条件推测性十进制加法器时,完成加6预操作之后十进制进位和二进制相应位的进位信号一致,因此在二进制加法器设计中广泛采用的并行前缀/进位选择结构可以用于十进制加法器的设计。文献[7-9]采用基于SK的QT树形结构产生进位信号。典型的16 bit SK结构如图4所示,SK树的逻辑级数最小,为,运算结点只有个。但是SK树形结构随着操作数位数的增大,其最大扇出数呈线性增长,导致延迟时间增大。为了获得高性能的十进制加法器,采用基于KS的并行前缀/进位选择加法器结构设计32 bit, 64 bit和128 bit十进制加法器,并对4 bit十进制进位选择加法器进行优化设计。典型的16 bit KS结构如图5所示。
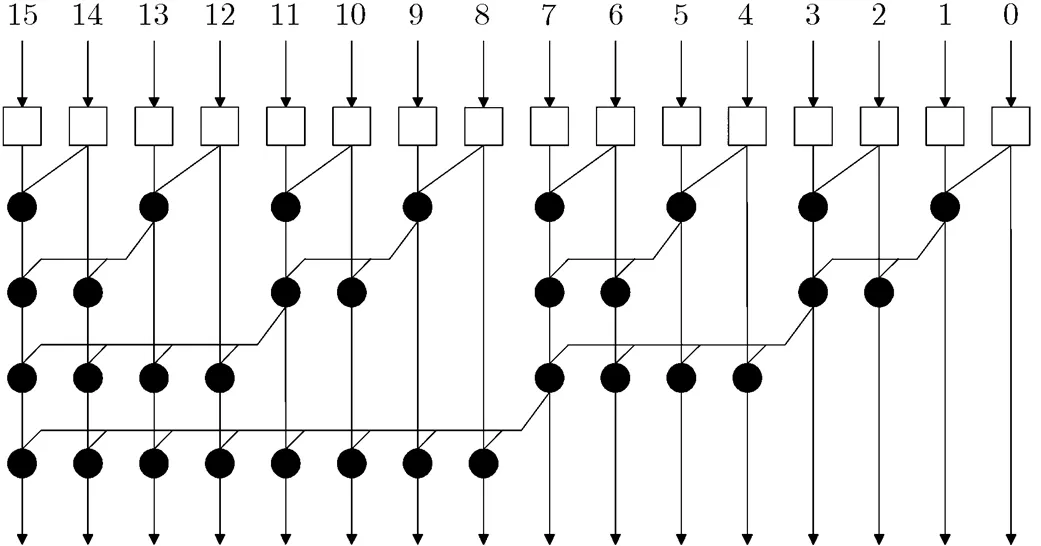
图4 典型16bit Sklansky前缀结构
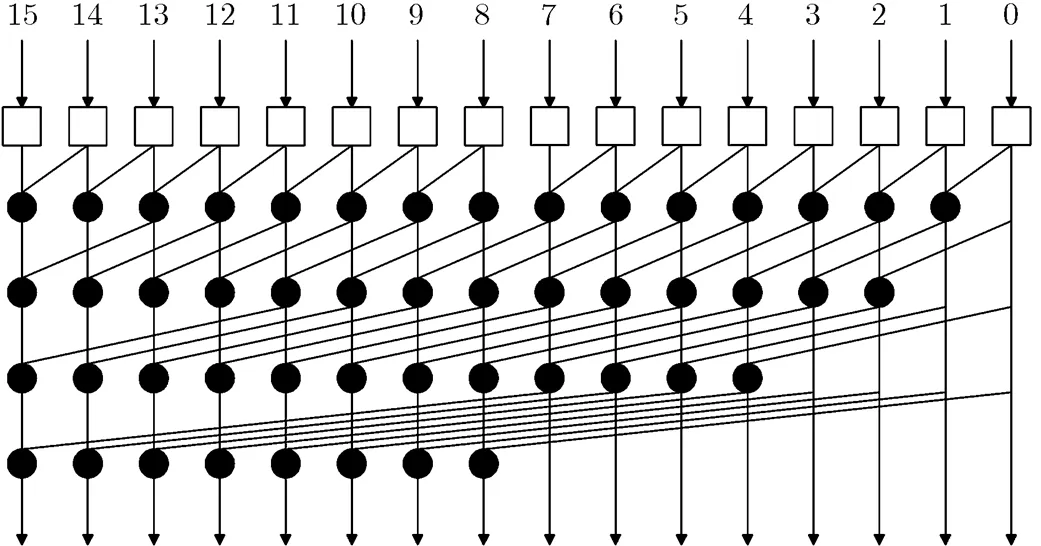
图5 典型16bit Kogge-Stone前缀结构
为了减少加法器的复杂度,本文将利用并行前缀单元对文献[7]中的十进制进位选择单元进行改进。令,为相应的十进制进位输出信号,当时,运算结果无需修正;当时,不管等于0或者1,,和与无关。定义是0位和1位的方块进位产生信号,是0位和1位的方块进位传递信号;定义是0位、1位和2位的方块进位产生信号,是0位、1位和2位的方块进位传递信号。则
由式(7)和式(8)得到改进的十进制进位选择加法器如图6所示。
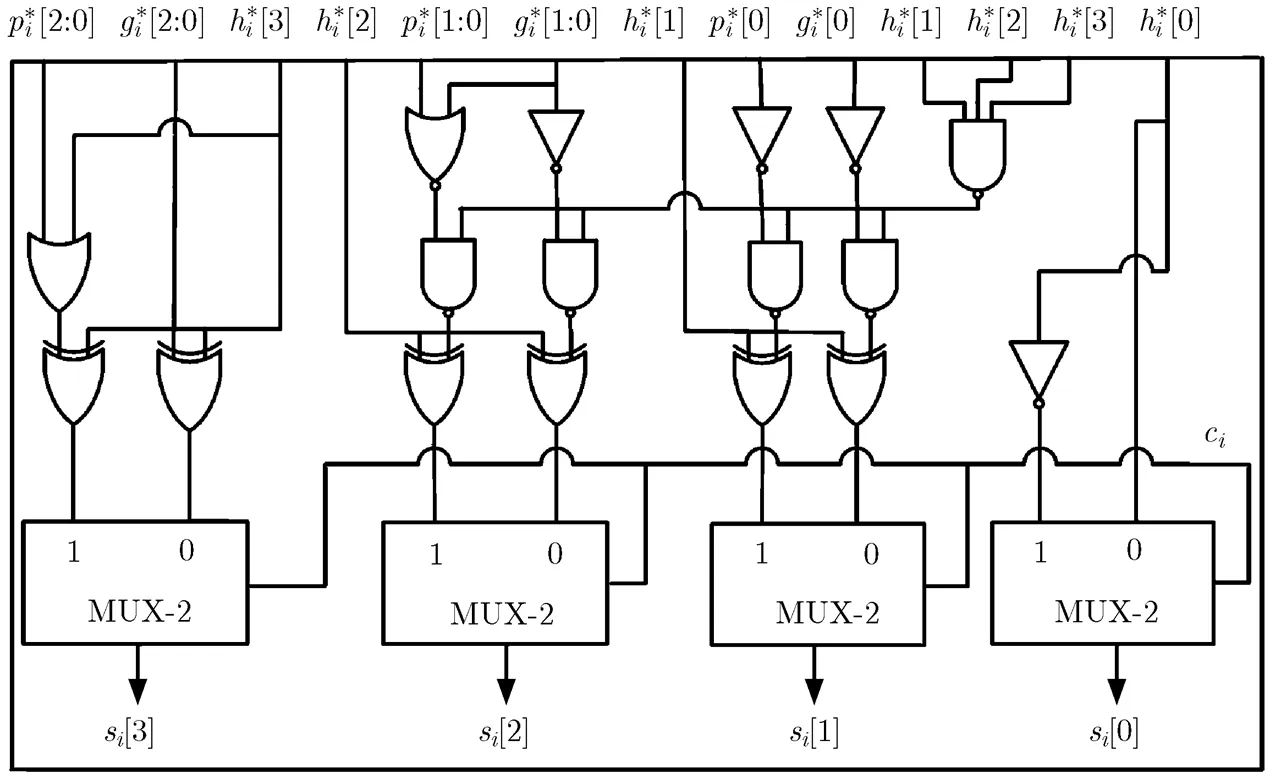
图6 改进的十进制进位选择加法器单元
32 bit基于KS结构的并行前缀/进位选择加法器由8 bit KS结构的并行前缀加法器扩展得到,产生的7个进位输出信号作为十进制4 bit进位选择加法器单元进位选择信号。改进的32 bit基于KS结构的并行前缀/进位选择十进制加法器如图7所示。图7中的十进制进位选择加法器模块如图6所示。由图6和图7可以看到,充分利用并行前缀中已经存在的方块进位产生信号和方块进位传递信号来简化十进制进位选择加法电路,避免在进位选择加法器中重复计算,可以减小电路的复杂度。
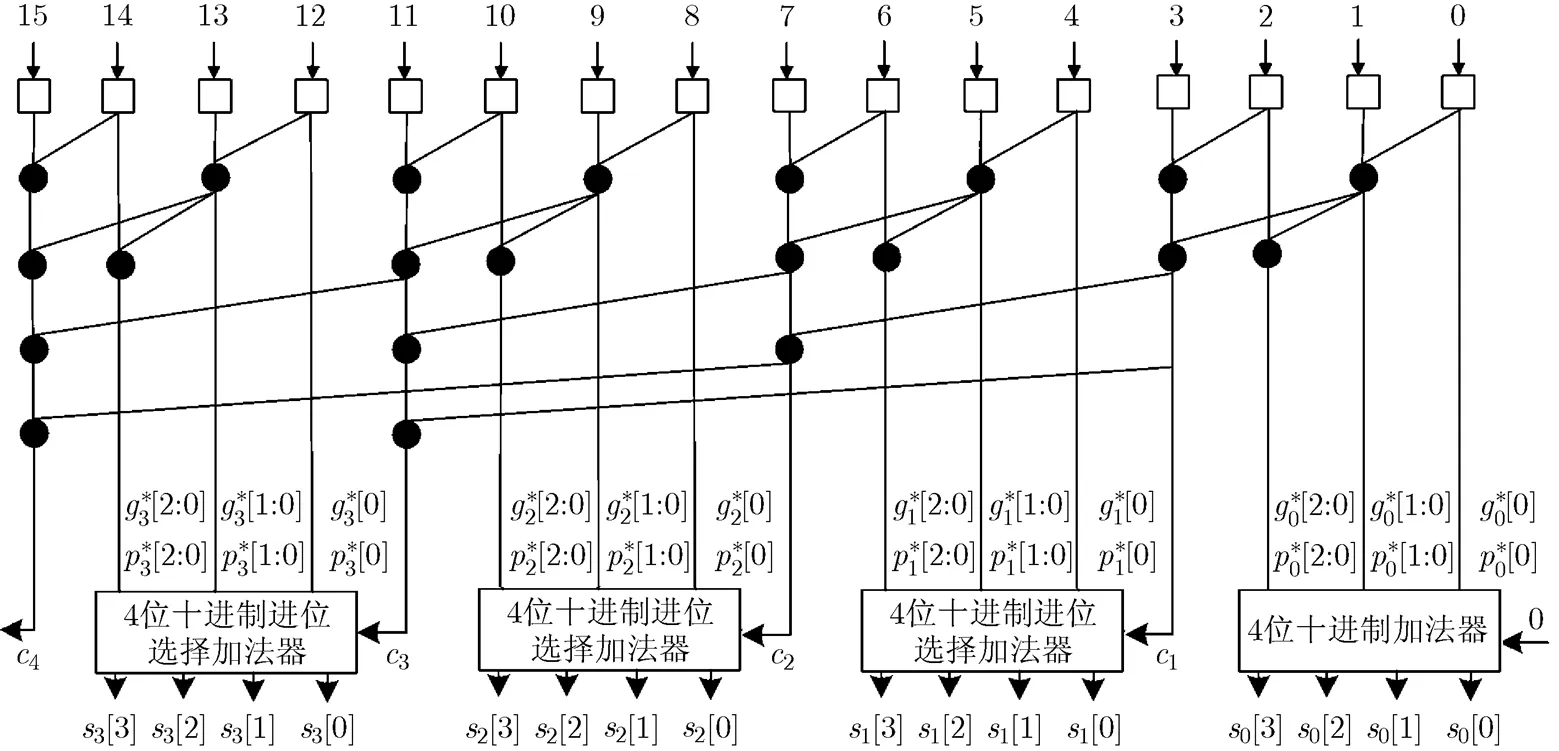
图7 改进的16bit基于KS并行前缀/进位选择结构条件推测性十进制加法器
4 实验结果
64 bit基于KS结构的并行前缀/进位选择加法器由16 bit KS结构的并行前缀加法器扩展得到,产生的15个进位输出信号作为十进制4 bit进位选择加法器单元进位选择信号,128 bit基于KS结构的并行前缀/进位选择加法器由32 bit KS结构的并行前缀加法器扩展得到,产生的31个进位输出信号作为十进制4 bit进位选择加法器单元进位选择信号。使用Verilog HDL硬件描述语言分别对32 bit, 64 bit和128 bit基于并行前缀/进位选择结构的条件推测性十进制加法器进行描述。在NanGate Open Cell 45nm CMOS标准工艺库下,通过Synopsys公司综合工具Design Compiler进行综合,获得延时和面积,采用Synopsys Power Compiler获取功耗。最终得到本文提出的32 bit, 64 bit, 128 bit十进制加法器,基于KS结构的二进制并行前缀/进位选择加法器[17]和文献[9]中的电路结构的延迟、面积、功耗参数结果如表1所示。延时对比和延时-功耗积对比如图8和图9所示。
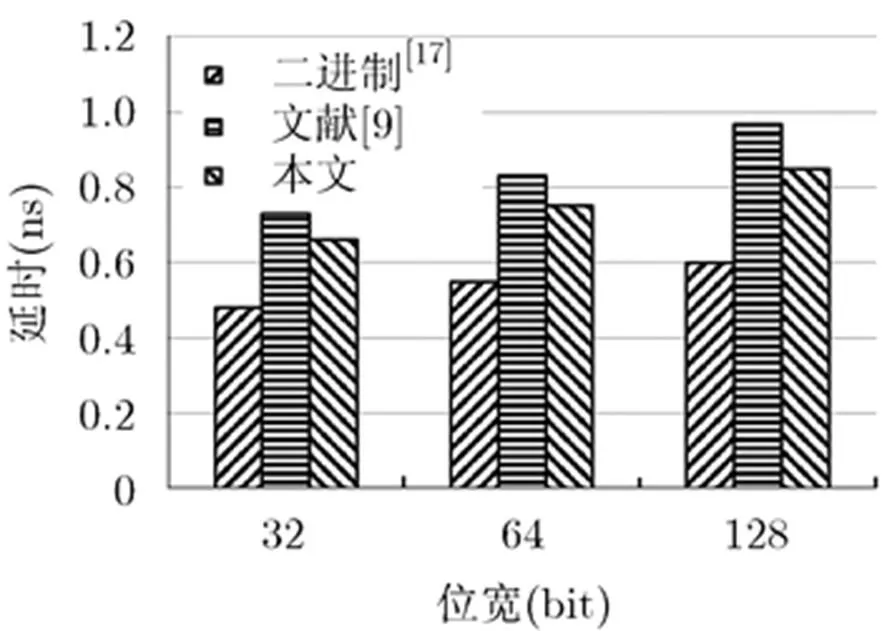
图8 改进的十进制加法器与文献[9]和文献[17]的延时对比
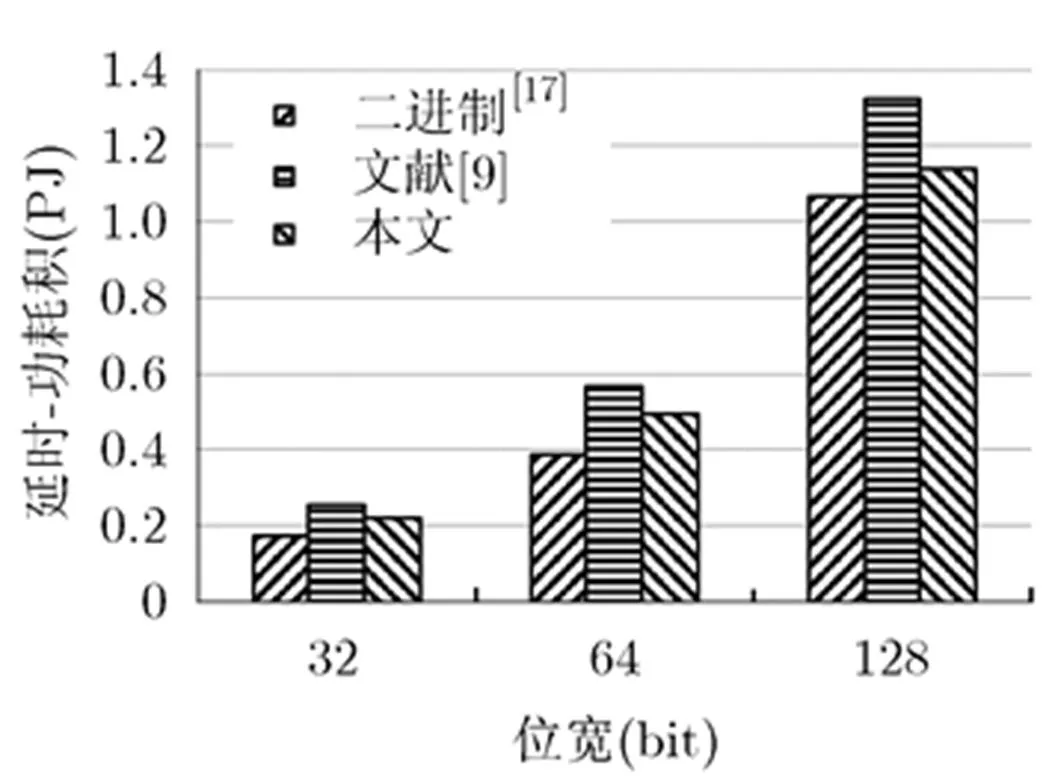
图9 改进的十进制加法器与文献[9]和文献[17]的延时-功耗积对比
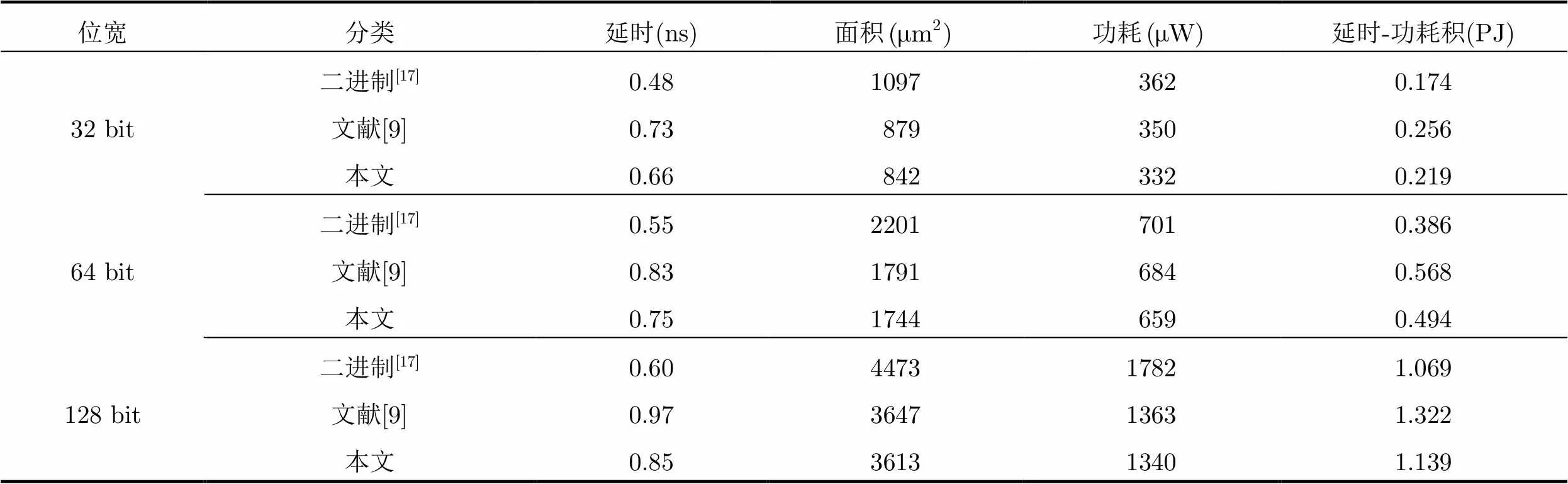
表1二进制、十进制加法器综合结果比较
从图8和图9对比结果可知,与文献[9]所采用的加法器结构相比较,在不增加面积和功耗的情况下,本文提出的32 bit, 64 bit和128 bit十进制加法器的延迟分别降低9.5%, 9.6%和12.3%,随着位宽的增加,速度提高的效果更加明显。其延时-功耗积分别减少了14.5%, 13.0%和13.8%,其性能得到有效的改善。
与基于KS结构的PPF/CSL的二进制加法器相比较,本文提出的32 bit, 64 bit和128 bit十进制加法器的延时-功耗积分别增加了25.9%, 28.0%和6.5%。从综合结果来看,十进制加法器的速度低于二进制加法器。需要说明的是,十进制加法器和二进制加法器的综合结果的比较仅具有参考意义,目前十进制算术运算只是应用于商业和金融等高精度计算领域,它并不能取代二进制算术运算。
5 结束语
条件推测性十进制加法器可以有效地完成十进制加法器运算,本文采用基于KS结构的PPF/CSL加法器构成条件推测性十进制加法器,并对4 bit进位选择单元进行优化设计,利用并行前缀中的方块进位产生信号和方块进位传递信号来简化十进制进位选择加法的电路。从实验结果看出,本文提出的32 bit, 64 bit和128 bit十进制加法器相比较于文献[9]中的电路结构延时-功耗积分别降低了14.5%, 13.0%和13.8%。本文提出的条件推测性十进制加法器的性能得到了有效的提升。
参考文献
[1] IEEE Std 754(TM)-2008. IEEE standard for floating-point arithmetic[S]. IEEE CS, 2008. doi: 10.1109/ieeestd.2008. 4610935.
[2] EISEN L, WARD J W, TAST H W,. IBM POWER6 accelerators: VMX and DFU[J]., 2007, 51(6): 663-684.doi: 10.1147/rd.516.0663.
[3] SCHWARZ E M, KAPERNICK J S, and COWLISHAW M F. Decimal floating-point support on the IBM system z10 processor[J]., 2009, 53(1): 4:1-4:10.doi: 10.1147/JRD.2009.5388585.
[4] WANG L K, ERLE M A, TSEN C,. A survey of hardware designs for decimal arithmetic[J]., 2010, 54(2): 8:1-8:15.doi: 10.1147/ JRD.2010.2040930.
[5] SCHMOOKLER M and WEINBERGER A. High speed decimal addition[J]., 1971, 20(8): 862-866.doi: 10.1109/T-C.1971.223362.
[6] LIU Han, ZHANG Hao, and SEOK-BUM Ko. Area and power efficient decimal carry-free adder[J]., 2015, 51(23): 1852-1854. doi: 10.1049/el.2015.0786.
[7] VAZQUEZ A and ANTELO E. Conditional speculative decimal addition[C]. Proceedings of Seventh Conference on Real Numbers and Computers, Nancy, France, 2006: 47-57.
[8] VAZQUEZ A, ANTELO E, and MONTUSCHI P. Improved design of high-performance parallel decimal multipliers[J]., 2010, 59(5): 679-693.doi: 10.1109/TC.2009.167.
[9] VAZQUEZ A, ANTELO E, and BRUGUERA J. Fast radix-10 multiplication using redundant BCD codes[J]., 2014, 63(8): 1902-1914. doi: 10.1109/TC.2014.2315626.
[10] KORNERUP P. Reviewing high-radix signed-digit adders[J]., 2015, 64(5): 1502-1505.doi: 10.1109/TC.2014.2329678.
[11] MOHANTY B K. Area-delay-power efficient carry-select adder[J].:, 2014, 61(6): 418-422.doi: 10.1109/TCSII. 2014.2319695.
[12] MATHEW S K, ANDERS M, KRISHNAMURTHY R K,. A 4 GHz 130 nm address generation unit with 32-bit sparse-tree adder core[J]., 2003, 38(5): 689-695.doi: 10.1109/JSSC.2003. 810056.
[13] KOGGE P M and STONE H S. A parallel algorithm for efficient solution of a general class of recurrence equations[J]., 1973, 22(8): 786-793.doi: 10.1109/TC.1973.5009159.
[14] BRENT R P and KUNG H T. A regular layout for parallel adders[J]., 1982, 31(3): 260-264.doi: 10.1109/TC.1982.1675982.
[15] SKLANSKY J. Conditional-sum addition logic[J]., 1960, EC-9(2): 226-231. doi: 10.1109/TEC.1960.5219822.
[16] HAN TACKDON and CARLSON D A. Fast area-efficient VLSI adders[C]. IEEE 8th Symposium on Computer Arithmetic, 1987: 49-56. doi: 10.1109/ARITH.1987.6158699.
[17] DIMITRAKOPOULOS G and NIKOLOS D. High-speed parallel- prefix VLSI Ling adders[J]., 2005, 54(2): 225-231.doi: 10.1109/TC.2005.26.
[18] HE Yajuan and CHANG C H. A power-delay efficient hybrid carry-lookahead/carry-select based redundant binary to two’s complement converter[J].&:, 2008, 55(1): 336-346.doi: 10.1109/TCSI.2007.913610.
Design of Optimized Conditional Speculative Decimal Adders
CUI Xiaoping WANG Shumin LIU Weiqiang DONG Wenwen
(,&,210016,)
There are increasing interests in hardware support for decimal arithmetic due to the demand of high accuracy computation in commercial computing, financial analysis, and other applications. New specifications for decimal floating-point arithmetic have been added to the revised IEEE 754-2008 standard. In this paper, the algorithm and architecture of decimal addition is studied comprehensively. A decimal adder is designed by using the parallel-prefix/carry-select architecture. The parallel-prefix unit is used to optimize the decimal carry select adder. The decimal adder has been realized by Verilog HDL and simulated with ModelSim. The synthesis results of this design by Design Compiler is also given and analyzed under Nangate Open Cell 45nm library. The results show that the delay performance of the proposed circuit can be improved by up to 12.3%.
Decimal addition; Conditional speculative decimal addition; Parallel prefix; Carry select adder
TN431.2
A
1009-5896(2016)10-2689-06
10.11999/JEIT151416
2015-12-14;改回日期:2016-06-08;网络出版:2016-07-19
崔晓平 wnhcxp@nuaa.edu.cn
崔晓平: 女,1962年生,副教授,硕士生导师,研究方向为数字集成电路设计和计算机算术运算系统.
王书敏: 男,1990年生,硕士生,研究方向为数字系统设计与计算机应用.
刘伟强: 男,1983年生,副教授,硕士生导师,研究方向为数字集成电路设计和加密硬件.
董文雯: 女,1993年生,硕士生,研究方向为数字系统设计与计算机应用.
