一种基于整数小波变换的彩色图像盲水印技术
2010-07-05石红芹吕方亮
石红芹,吕方亮
(华东交通大学 软件学院,江西 南昌 330013)
在网络环境中实施有效的版权保护和信息安全是目前人们特别关注的1个问题。数字水印作为一种能够比较有效实施版权保护和信息安全的技术而成为1个新的研究热点。
从1993年Tirkel等人[1]提出了数字水印的一种方法以来,就不断的有数字水印算法涌现出来。现有方法[2,3]大致可分为空间域方法和变换域方法两个方面。整数小波变换作为新一代图像压缩标准JPEG 2000的核心部分已经被广泛应用,整数小波变换的优点在于能够在图像分解和重构过程中,保证图像在变换部分损失为0,从而提高嵌入水印的质量。根据水印在提取时是否需要原始载体又可将水印分为盲水印和非盲水印。在网络环境中,非盲水印的提取是不方便和不现实的。因此盲水印是更为实用的方案,同时越来越多的数字作品都是由非灰度图像构成的,所以对彩色图像水印的研究成为水印研究的热点。
1 彩色空间可逆整数变换
在PAL彩色电视制式中使用YUV模型,其中Y表示亮度,U,V用来表示色差,U,V是构成彩色的两个分量。YUV表示法的重要性是它的亮度信号(Y)和色度信号(U,V)是相互独立的,也就是由Y信号分量构成的黑白灰度图与用U,V信号构成的另外两幅单色图是相互独立的。由于Y,U,V是独立的,所以可以对这些单色图分别进行编码。此外,黑白电视能接收彩色电视信号也就是利用了YUV分量之间的独立性。
YUV表示法的优点是可以利用人眼的特性来降低数字彩色图像所需要的存储容量。人眼对彩色细节的分辨能力远比对亮度细节的分辨能力低。若把人眼刚能分辨出的黑白相间的条纹换成不同颜色的彩色条纹,眼睛就不再能分辨出条纹来。由于这个原因,就可以把彩色分量的分辨率降低而不明显影响图像的质量,因而就可以把几个相邻像素不同的彩色值当作相同的彩色值来处理,从而减少所需的存储容量。
对载体图像(彩色图像)进行彩色空间整数变换。当载体还原时还要通过彩色空间整数逆变换处理,所以这里介绍算法中的彩色空间可逆整数变换。根据HVS水印策略,人眼对亮度的信息不太敏感,而一般的彩色图像采用RGB彩色空间来表示一幅图像。所以,首先要将彩色图像由RGB彩色空间转换到YUV彩色空间以得到亮度Y分量。YUV彩色空间与RGB空间的转换关系见式(1)。

式中:Y表示亮度;U,V用来表示色差;R,G,B分别红绿蓝。
在上述关系中,R,G,B的值为整数(0-255),但由于转换的系数矩阵不是整数,因此Y,U,V的值也不是整数。为了得到整数,在这将Y,U,V的值都乘以1 000并取整,假设取整后的变量为KY,KU,KV,则可得到转换关系式(2)。
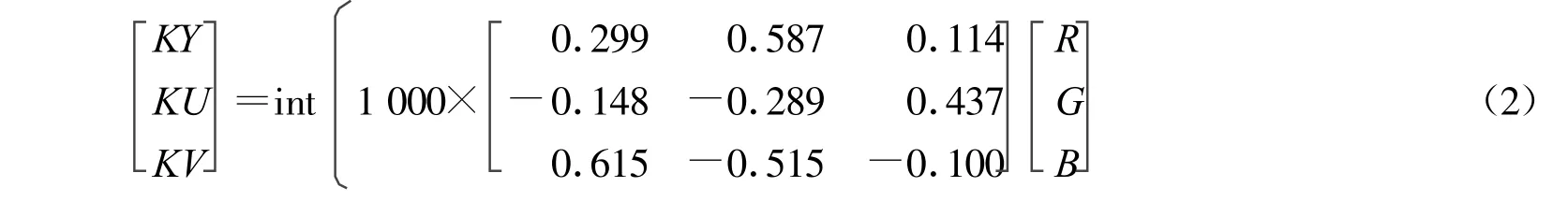
式中:int[◦]为取整运算。
通过式(2)就可以建立R,G,B与KY,KU,KV之间的整数到整数的可逆变换,它们的逆变换如式(3)。
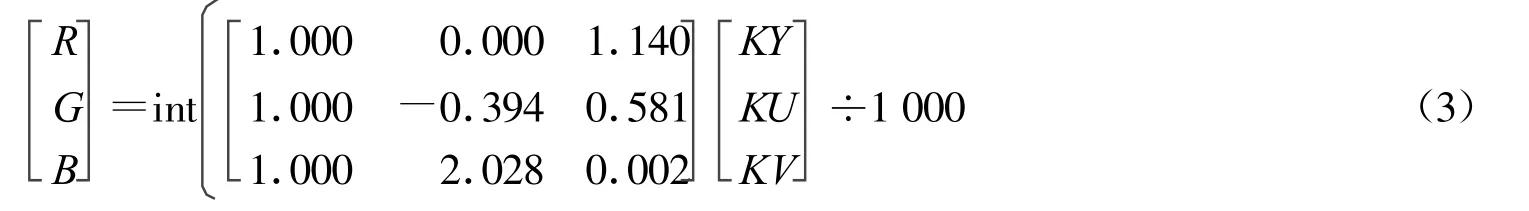
彩色空间可逆整数变换用于对载体图像的预处理(载体图像为彩色图像)。这主要是根据人类视觉系统(HVS)的特性,人眼对YUV空间中亮度分量Y的敏感性低于RGB彩色空间中各个颜色分量的敏感性。这样将水印信息嵌入到Y分量中具有较高的鲁棒性。采用整数可逆转换是由于在接下来的水印嵌入中,将用到离散整数小波变换,故先要得到1个整数的预处理域KY。
2 可逆离散整数小波变换
整数小波分解就是把数字图像在不同尺度的频率上进行分解和重构[4]。经过二维离散小波多分辩率分解以后,原始数字图像被分解成具有水平、垂直和对角方向在不同分辨率下的多个高频图,水平和垂直方向的低频子带图LL1、水平方向的低频和垂直方向的高频子带图LH1、水平方向的高频和垂直方向的低频子带图HL1以及水平和垂直方向的高频子带图HH1。若对子带图LL1再进行小波分解,又可以得到更低分辨率的4个子带图像,如此反复,可对数字图像进行多级小波分解得LHj,HLj,HHj和LLj。其中LLj表示由小波变换分解级数决定的最大尺度、最小分辨率下对原始图像的最佳逼近,称为小波变换子图,它集中了原始图像的绝大部分能量,其系数分布、统计特性与原始图像相似,有较好的稳定性。HHj表示了原始图像的水平边缘细节、垂直边缘细节和斜边缘细节信息,称其为高频子图。而LHj和HLj则是介于HHj与LLj之间的,可以称其为中频子图。一般我们将高频子图和中频子图统称为小波细节子图。细节子图的大部分能量集中在原始图像的边缘、轮廓、纹理信息对应的一些小波系数上。低频域LLj可以不断的分解下去,直到满足一定的分辨率要求。图1分别给出了对二维信号进行二维离散小波1级、2级的分解结果示意图。本文算法将水印信息嵌入到小波分解的低频域[5],即LLn(n表示小波分解的级数)。
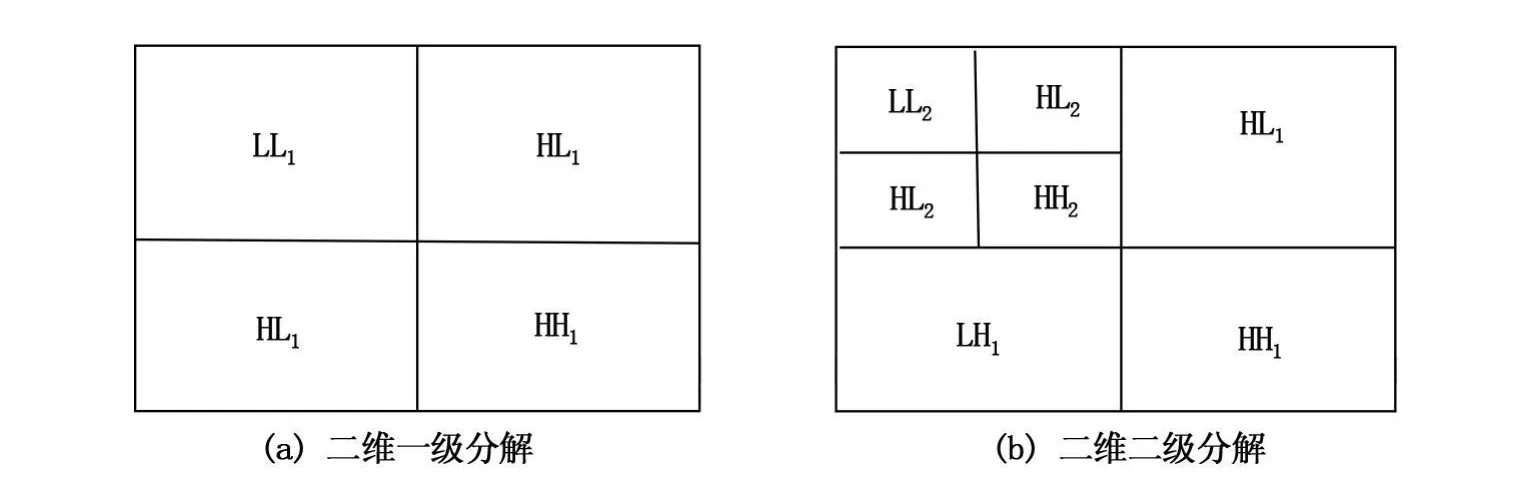
图1 二维小波分解示意图
在选择小波分解级数n时有两种选择策略:一是根据要嵌入的水印信息选择小波分解的级数,另一种是根据小波分解的级数选择嵌入水印的信息量[6]。本算法中采用的是后者即用于有意义二值图片的嵌入算法,根据小波分解的级数自动调整二值图片的大小以满足嵌入要求,同理,分解级数越大,则二值图片会被调整的越小,反之则越大。
3 彩色图像盲水印算法
该文提出了一种在彩色图像Y分量的离散小波变换(DWT)域嵌入水印的方案。提取原始载体图像的KY(经过取整后的Y)分量,利用离散小波变换将其进行小波分解,得到不同空间、不同分辨率的子带图像。选择在子带图像LLn中嵌入水印,其优点是经小波分解后,KY分量的绝大部分能量都集中在LLn中,其系数的值非常大,在其中嵌入水印的强度可以适当加大,而不影响图像的视觉效果。在LLn中嵌入水印,经受各种攻击后水印的顽健性最好。
3.1 水印的嵌入和提取
原始载体图像分别是512×512的真彩色测试图像,如图2所示。首先将原始载体图像进行彩色空间转换(由RGB转换到YUV)提取KY分量进行整数小波变换,得到低频分量LLn,然后按式(4)求LLn的平均能量E,并对LLn的系数平方值按大小排序。根据LLn的系数的平方值与E值的比值关系,确定嵌入水印的强度。比值越大,可以隐藏的水印强度越大。用E表示低频子带LLn的能量,其计算公式见(4)。

式中:X(i,j)表示子带图像LLn中(i,j)位置像素的值。对X(i,j)按大小值排序,得到一维序列X'(k),k=1~128×128。水印嵌入强度由公式(5)确定。

水印的嵌入公式见(6)

水印提取是水印嵌入的逆过程,具体提取过程如下。
(1)先对可能被破坏的含水印图像进行可逆整数彩色空间转换,得到YUV彩色空间的KY′分量,然后对KY′分量进行相应级数的整数小波分解得到低频域LLn′;
(2)对于子带LLn′通过计算提取水印,得到用0,1表示的水印信息。再结合水印处理过程将得到的信息还原即得到可能已经失真的水印。
4 实验结果
4.1 水印对原图质量的影响
水印不可见性是数字水印研究的1个重要内容。在这里进行水印嵌入对原图像质量的比较,比较参数使用峰值信噪比(PSNR)来评价原始图像与含水印图像间的差别,PSNR值越大,不可感性越好.水印的原图为同1张图像,见图3。对同1张载体图像分别在不同小波分解级数下进行比较。根据前面提出的算法[7],不同级数嵌入的水印图像在水印原图的基础上自动调整大小以适应嵌入域的大小。共选择7张不同的水印标准图像作为载体,它们分别是狒狒、F16、渔船、丽娜、歌剧院、辣椒和水,见图2。

图2 载体原始图像

图3 水印原始图像
测试时,先将选中的7张图片分别调整到512×512大小,然后分别在每张图片的1到5级小波域中嵌入水印图片,获得每次嵌入水印后的图像的峰值信噪比(PSNR),结果见表1。在此列举其中的1幅图片水印的嵌入效果图,见图4,图中从左到右分别是1级、2级、3级、4级以及5级小波分解域中嵌入水印的效果。

图4 水印嵌入效果图
从图4以及表1中可看出,本文所提出的算法对原图质量的影响较小,故该水印算法是有效的。

表1 水印对图像的影响PSNR值 dB
4.2 可抵抗JPEG压缩攻击
水印原图见图3,载体的原始图像为上述7张图片,见图2。载体的大小先调整为512×512,先分别将水印嵌入到7张图的小波1级分解域中,然后对嵌入后的图像进行JPEG压缩,即将图片存储为jpg格式。然后分别从jpg格式的图片中提取出水印图片。最终嵌入的水印图片见图5,压缩域提取出来的水印见图6,在图6中,从左到右分别是从狒狒、F16、渔船、丽娜、歌剧院、辣椒及水的JPEG压缩图片中提取出来的水印。
从图6可知,该水印算法可抵抗JPEG压缩攻击。

图5 嵌入的水印

图6 JPEG压缩后提取出的水印
5 结论
基于离散整数小波变换的水印图像对原图质量的影响较小且可抵抗JPEG压缩攻击,具有抗篡改性和可证明性的优点。另外水印的提取并不需要原始载体图像的参与,实现了真正意义上的盲水印提取。对有意义二值图片的嵌入与提取结果较为理想,而对有意义字符串嵌入与提取还需要进一步的研究与改善。一方面是由于字符串本身的精确性,只要有一位二进制位发生变化,字符串就会发生改变;另一方面是由于在提取时字符串信息不象二值图片容易定位。
[1]COX I J,MILLERM L.The first 50 years of electronic water-marking[J].Journal of Applied Signal Processing,2002(2):126-132.
[2]SWELDENS W.The lifting scheme:a custom-design construction of biorthogonal wavelets[J].Applied and Computational Harmonic Analysis,2001,3(2):186-200.
[3]DAUBECHIES I,SWELDENS W.Factoring wavelet transforms into lifting step[J].Journal of Fourier Analysis and Applications,1998,4(3):247-269.
[4]吴永宏,潘泉,张洪才,等.基于提升框架的整数小波变换[J].电子与信息学报,2004(4):659-663.
[5]张晓黎.基于整数小波变换的盲数字水印算法[J].计算机应用与软件,2007(4):32-34.
[6]郝小峰,孙德辉.基于整数小波变换和零树编码的监控图像压缩[J].微计算机信息,2006(10):287-289.
[7]范宇,胡访宇,赵爱华.基于整数提升小波变换图像压缩的优化与实现[J].计算机工程与应用,2004(8):81-82.
