基于粒子群的蚁群算法参数最优组合研究
2010-07-05俞云新王更生
俞云新,王更生
(华东交通大学信息工程学院,南昌江西330013)
Yu Yunxin,Wang Gengsheng
(School of Information Engineering,East China Jiaotong University,Nanchang 330013,China)
自1991年Dorigo,Maniezzo和Colorni等首先提出蚁群算法[1,2]以来,很多研究人员对该算法进行了研究,并成功地解决了许多组合优化问题,如TSP问题,即在给定城市个数和各城市之间距离的条件下,找到一条遍历所有城市且每个城市只访问一次的总路程最短的路线。蚁群算法在TSP问题应用中取得了良好的效果,但参数α,β,ρ,Q,m的设置不当可能导致算法求解速度很慢且所得解的质量特别差,对此问题,已有研究人员进行了研究,但还没有可行的方案。本文将在已有研究成果的基础上,对此问题进行研究。
1 蚁群算法基本原理
蚁群算法模型可以通过TSP(旅行商)问题描述[3],TSP问题是指完全遍历 n个城市一次且仅一次所走过的最短距离。其数学模型如下。
首先引入如下符号,m表示算法中蚂蚁的数量;dij(i,j=1,2,…,n)表示边(i,j)之间的距离;n为城市个数;τij(t)表示t时刻在(i,j)上残留的信息素量。初始时刻,各边信息素量相等。蚂蚁k在t时刻由城市i转移到城市j的概率为

式中:ηij为先验知识或能见度,针对具体问题根据启发式规则而定;α为边(i,j)上残留信息的重要程度;β为启发信息的重要程度;tabuk为蚂蚁k的禁忌表即蚂蚁k所走过的城市集。
随着时间的推移,以前蚂蚁留下的信息素逐渐消逝,用参数ρ(ρ∈(0,1))表示信息素挥发率,当蚂蚁完成一次循环后,各路径上的信息素量根据下式做调整
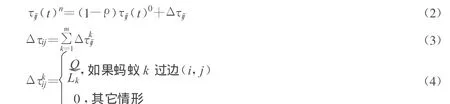
式中:τij(t)n表示更新后边(i,j)上的信息素量;τij(t)o表示更新前边(i,j)上的信息素量;Δτkij表示第k只蚂蚁本次循环中留在边(i,j)上的信息素量;Δτij表示本次循环中边(i,j)上信息素增量;Q为常数;Lk表示第k只蚂蚁在本次循环中所走过的路径长度。当所有蚂蚁都完成一次周游后,因每只蚂蚁本次周游的禁忌表已满,此时应及时清空,准备下一次周游。当周游次数达到设定值时算法结束。
经过十几年的发展,蚁群算法有诸多改进算法[4],但息启发式因子α、期望值启发式因子β、信息素挥发因子ρ、蚂蚁数量m和初始信息素量Q都始终是影响算法性能的重要参数,其中 α的大小反映了信息素因素的作用强度,β反映了先验性、确定性因素的作用。ρ的大小直接关系到蚁群算法的全局搜索能力及收敛速度。此外,m和Q也是影响算法效率的重要参数。有研究成果表明[4],参数的不同取值对算法性能的影响较大,为确定使算法性能较佳的最佳组合参数,本文将提出一种解决方案。
2 “两步走”参数最优组合确定策略
本文试图确定蚁群算法参数的最佳组合,使得算法性能最佳,在现有研究成果的基础上,提出“两步走”策略,即利用基本蚁群算法确定各参数的范围,再引入适应度函数并结合粒子群算法确定各参数的最优组合。本节将先简单介绍粒子群优化原理,再介绍“两步走”策略方案,最后叙述基于粒子群的蚁群算法参数最优组合确定算法。
2.1 粒子群优化原理
粒子群优化(Particle Swarm Optimization,PSO)[5]是由Kennedy和Eberhart借鉴鸟类寻找食物的自然现象提出的一类基于种群的随机全局优化技术。在算法的每一次迭代中,粒子xi通过跟踪其自身所找到的最优解(个体极值pbest)和整个种群目前找到的最优解(全局极值gbest),按式(5)来进行更新,从而引导粒子向最优解方向移动。
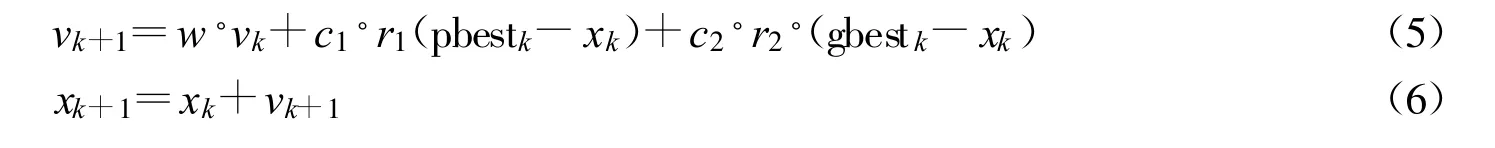
式中:vk是粒子的速度向量;xk是当前粒子的位置;c1,c2为常数,称为学习因子;r1,r2是在(0,1)上均匀分布的随机数;w是惯性权重。
粒子群算法的优点是简单易实现,比较适合解决连续域组合优化问题。
2.2 “两步走”策略具体步骤
第1步 根据基本蚁群算法,确定各参数较优范围。已有研究成果[5-10]得到各参数的经验值,即α=1,β=5,ρ=0.5,m=n/1.5(n为城市数),Q=100。根据专家给出的参数可取范围,利用基本蚁群算法,确定各参数的较优区间。在计算某个参数时,其余参数均采用经验值。
第2步 引入适应度函数概念,结合粒子群算法,确定蚁群算法参数的最佳组合,使算法性能得到提高。理论思想是将蚁群算法抽象为一个函数F,参数α,β,ρ,Q,m抽象为函数的自变量,因此参数的组合优化问题可定义为:确定自变量 α,β,ρ,m,Q的最佳组合,使函数F(α,β,ρ,m,Q)取得最优值。由于参数的组合优化问题是一个连续域的组合优化,所以本文采用前面介绍过的粒子群算法来确定各参数的最佳组合,详细算法将在下文阐述.
2.3 基于粒子群的蚁群算法参数最优组合算法设计
为实现“两步走”策略的实际应用,本文提出基于粒子群的蚁群算法参数最优组合算法,其思想是将蚁群算法参数作为粒子群算法的优化对象(粒子的位置),在每一次迭代过程中,使用粒子的当前位置信息来运行蚁群算法求解一标准优化问题,并使用适应度函数F(α,β,ρ,m,Q)对求解性能做出评价,从而引导各粒子向着最优的方向飞翔。算法的运算步骤如下。
步骤1 根据“两步走”策略中的第一步,确定各参数的较优区间,编写基本蚁群算法程序,将参数 α,β,ρ,m,Q作为入口参数以便调用。另外,为了保证数据的合理性,程序输出的结果取每一组参数十次运行的平均值。
步骤2 设定学习因子c1,c2和惯性权重w,在各参数较优区间内,对各粒子的初始位置和速度进行随机选取;
步骤3 使用每个粒子对应的位置信息运行蚁群优化算法,求解一标准优化问题,并使用适应度函数F(α,β,ρ,m,Q)对求解结果进行评价,得到各粒子的适应值;
步骤4 对各粒子,比较其当前位置适应值和pbest的适应值,如果更好,则用当前位置来更新pbest;
步骤5 用每个粒子的pbest的适应值与全局极值gbest的适应值比较,若更好,则更新gbest;
步骤6 按式(5),(6)对每个粒子进行速度和位置更新;
步骤7 判断是否满足终止条件,若满足,则输出全局极值gbest及粒子位置,否则转到步骤3。
为验证本文提出策略及算法的实用性,下节将对结合实例对策略及算法进行仿真。
3 仿真结果及性能分析
本文根据TSP问题中的Eil51数据对算法做了仿真,用C++语言为确定蚁群算法参数最优组合设计了程序并进行运算。由于这两种算法均是集群算法,所以有大量的蚂蚁个体和粒子个体而且需要迭代运行产生优化结果。因此,编程实现中的难点是算法的时间开销问题。本文经过程序设计的优化,以及适当地减少迭代次数,使得程序在理想的时间内得到优化的结果。蚁群算法的迭代次数为300,粒子群算法的迭代次数为100,粒子群算法的参数值选为
w=1,c1=c2=2。
确定蚁群算法各参数较优区间。取 α的范围(0,10),步长为0.5;β的范围(0,10),步长为0.5;ρ的范围(0,1),步长0.05,m范围(30,50),步长为1,Q范围(0,500),步长为10,每次迭代1 000次。平均路径长度取10次运行结果的平均值。本文列出参数ρ对蚁群算法性能影响的结果表1及收敛趋势图1。
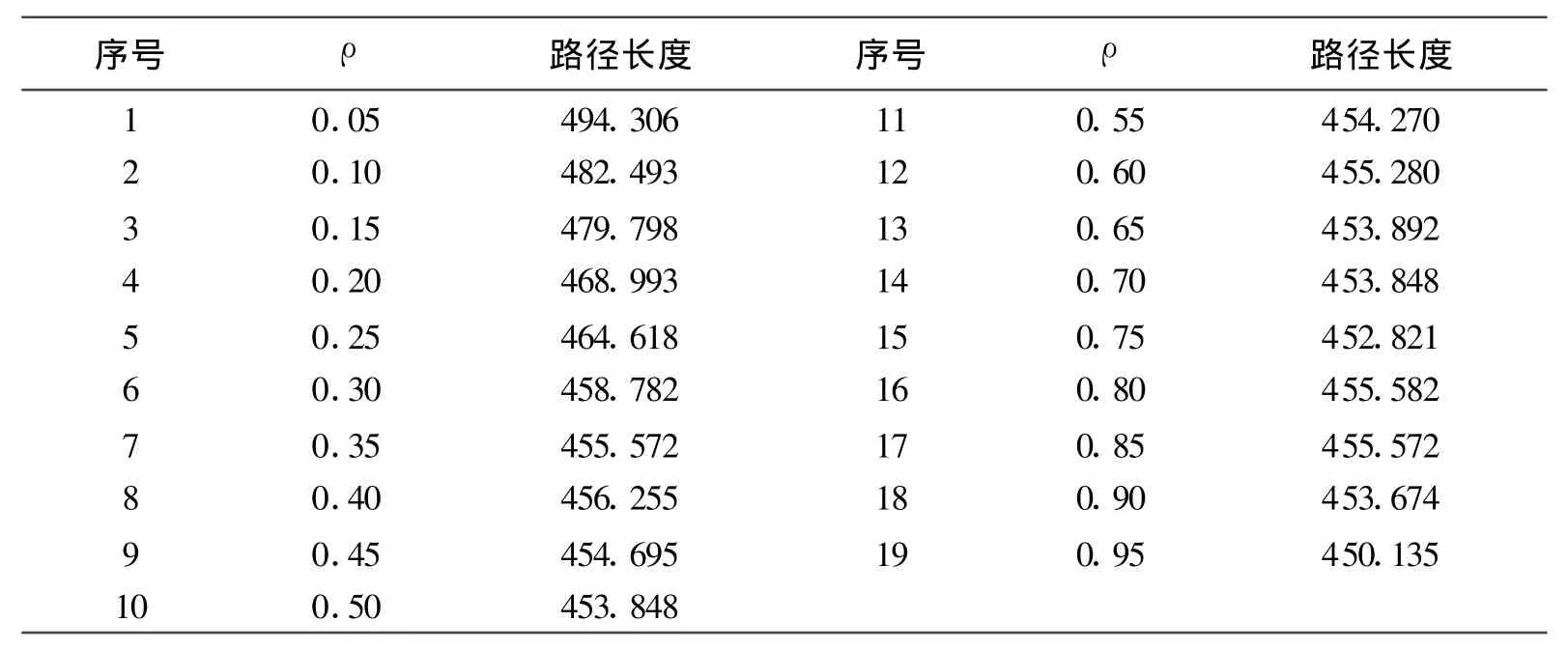
表1 ρ与平均路径长度的关系表
为进行对比,本文将蚁群算法各参数的随机组合得到的10个较优结果列于表2。

表2 蚁群算法参数随机组合结果表
根据本文提出的“两步走”策略得到的10个较优结果见表3。
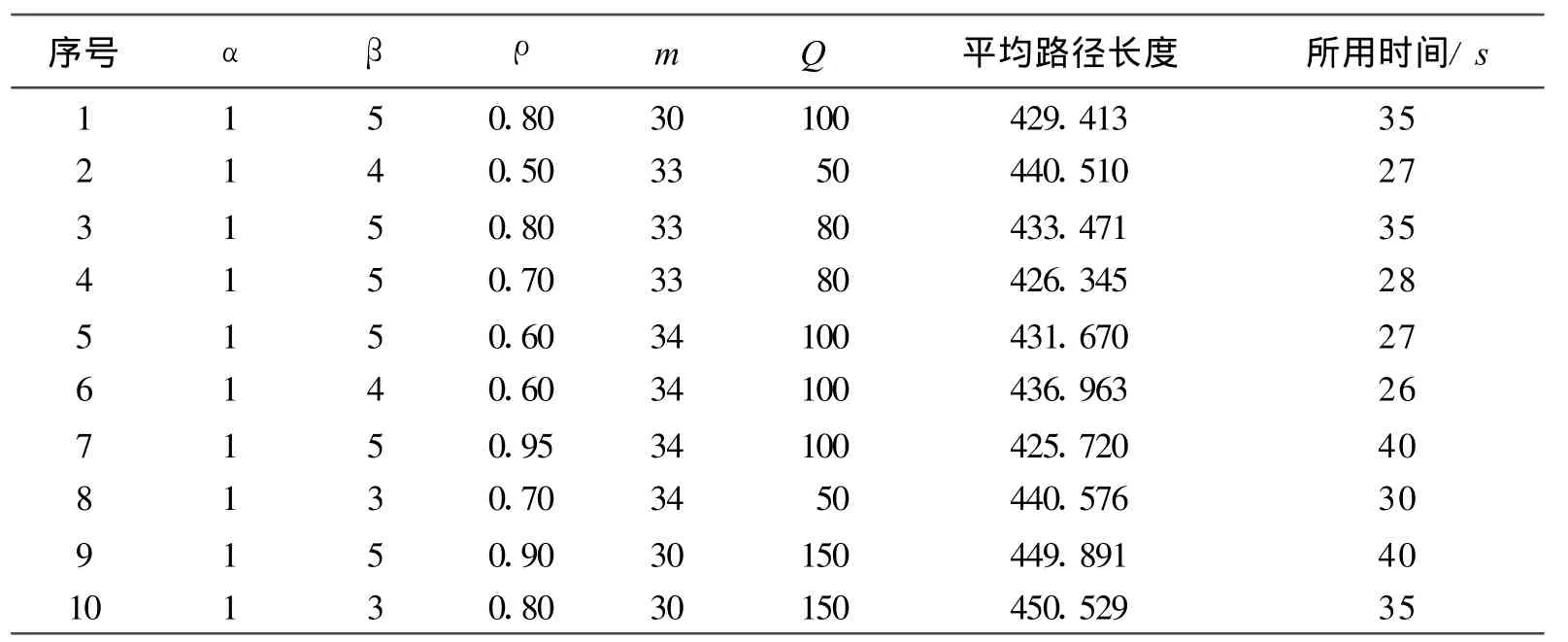
表3 基于粒子群的蚁群算法参数优化最优组合结果表
两组结果中最优路径的收敛趋势见图2。

图1 ρ与平均路径长度的关系
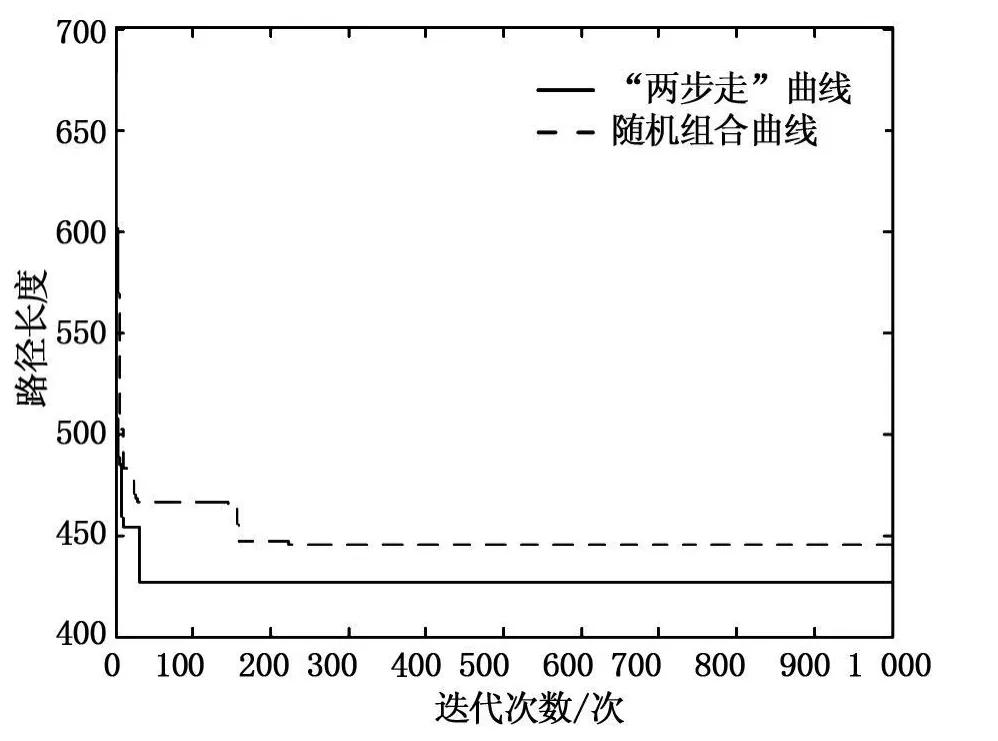
图2 两组最优结果的收敛趋势图
由表2可知,各参数的不同取值,对算法的性能有较大影响;较优区间内参数的随机组合,并不能使得算法的性能最佳。由表3可知,最佳组合的各参数值与各参数的经验值较接近,但性能有所差别,尤其是算法所花费时间差别比较大,因此,在解决实际问题中,要根据实际问题来确定各参数的值。其中,表3的第7行数据,最优结果值(425.720)比TSP官方公布的最优结果(TSP机构公布Eil51问题的最优结果是426)要好,但花费的时间较长。对比表2和表3可得,用“两步走”得到的参数最佳组合确实可以提高算法的性能,无论是时间还是最优解都比随机组合的结果要优。图2是两组结果中最优路径长度收敛趋势对比,它验证了表2和表3的对比结果。
4 结论
蚁群算法各个参数对算法性能有较大影响,参数间的随机组合使得算法陷入局部最优,花费时间过长等等。针对这一问题,本文提出了确定参数最优组合的“两步走”策略及基于粒子群的蚁群算法参数最优组合算法,通过TSP问题中Eil51问题进行仿真和结果比较,证明了本文提出的策略及算法可以克服蚁群算法随机参数的缺陷。本文策略及算法得到结果在最优值,稳定性和防止停滞方面都提取得了不错的效果,增强蚁群算法实用性,有利于蚁群算法推广及应用。
[1]BLUM C.Ant colony optimization:Introduction and recent trends[J].Physics of Life Reviews,2005,2(4):353-373.
[2]COLORM A,DORIGOM,MINIEZZO V.Distributed optimization by ant colonies[C].Proceeding of the First Europea n Conference on Artificial Life.ParisFrance:Elsevier Publishing,1991:134-142.
[3]劳眷.蚁群算法求解TSP问题若干改进策略的研究[J].科学技术与工程.2009,9(9):2 459-2 462.
[4]李士勇.蚁群算法及其应用[M].哈尔滨:哈尔滨工业大学出版社,2004:33-34.
[5]张江维,司文建.粒子群算法求解旅行商问题程序设计[J].电脑知识与技术,2009,5(7):1 696-1 698
[6]张毅,梁艳春.蚁群算法中求解参数最优选择分析[J].计算机应用研究,2007,24(8):70-72.
[7]段海滨,王道波,朱家强,等.蚁群算法理论及应用研究的进展[J].控制与决策,2004,19(12):1 322-1 340.
[8]杨中秋,张延华,郑志丽.基于改进蚁群算法对最短路径问题的分析与仿真[J].沈阳化工学院学报,2009,23(2):150-153.
[9]叶志伟,郑肇葆.蚁群算法中参数α、β、ρ设置的研究——以TSP问题为例[J].武汉大学学报,2007,29(7):597-601.
[10]蒋玲艳,张军,钟树鸿.蚁群算法的参数分析[J].计算机工程与应用,2007,43(20):31-36.
