基于二维激光扫描的煤场储量计算与显示
2010-07-05蒋先刚陶龙风马得安
蒋先刚,陶龙风,马得安
(华东交通大学 1.信息工程学院;2.基础科学学院,江西 南昌330013)
三维空间数据场的显示与计算是计算机图形学中一个重要的应用研究范围,它是分析和描述三维数据内部结构信息的有效方法。工厂煤储量的数据是一个变化的曲面体数据,通过实时的激光扫描,可将煤堆每一截面的顶部曲线数据获取,依据截面二维数据就可构建和显示出三维数据场。我们通过OLE自动化把测量的煤堆的自定义格式数据转换为通用格式的二维切片数据并转换为三维数据场以直观的效果图显示出来,通过三维数据的体积计算以获得煤场的储存量。
1 工厂煤体积估算系统的框架设计
工厂煤场体积测量系统主要功能模块包括图像摄入(即利用Lase激光系统测量二维横截面数据,且测量的精确度达到0.1 mm)、OLE自动化获取二维截面数据、用Marching Cubes和直接体绘制显示和计算三维曲面体体积。本文运行的环境是Windows XP操作系统,Delphi7开发平台,具体的软件流程如图1所示。

图1 煤堆体积估算与显示的软件流程图
2 煤场体积的计算方法
2.1 OLE自动化获取二维截面数据
通过Lase激光扫描硬件系统获得的数据一般以Excel格式保存,需要采用合理的接口文件得到这个三维扫描数据,因此需要利用客户程序(如工厂煤场的显示和测量估算三维重构系统)控制和访问服务器程序(Excel小型数据分析软件系统)这样的OLE自动化技术。OLE自动化的技术可使得客户程序能控制其他应用程序或DLL中的对象的属性和方法。典型的的OLE自动化服务器的例子是外部调用Excel和Word[1]。Excel即为一个服务器程序,它除了完成数据输入,计算排序等功能外,还提供供外部程序访问内部数据的对象、方法和属性。
本文中的三维重构程序作为客户程序通过OLE自动化技术访问服务器程序(Excel)的方法和属性,以读取不同y位置的Excel中每一截面的离散x,z坐标。由于本文涉及的Excel中的数据是用空格来分隔各组不同数据的,程序设计时以空格作为数据各字段的分隔标志进行分析。
2.2 Marching Cubes方法显示曲面体
三维数据体绘制技术可以分为两大类[2]:面绘制(Surface Rendering)和直接体绘制(Direct Volume Rendering)。面绘制技术是从3D数据场中抽取有意义和直观信息的一种重要手段。它实际上是把体数据转换成一种逼近面形式,从而可以进一步利用计算机图形的OpenGl的显示技术。直接体绘制技术是以某种方式将整个数据场半透明地投影到2D屏幕上,并不借助中间几何图形,在本系统设计中可快速显示二维截面的一般分布情况。Lase得到的数据只是煤堆截面的表面数据,它在显示曲面体时,通过将等值面上不完整立方体(如图2右上角所示小块)和曲面内完整的立方体(如图2左下角四方块)的体积累计就可获得曲面立方体的总体积。因此在进行体积计算时主要用到的重构方法采用Marching Cubes面绘制技术。
Marching Cubes[2]提出的有关算法主要针对三维规则网络数据提出,这类数据常见于计算机X光断摄影(CT)、磁共振(MR)、单光子发射计算机断层摄影(SPECT)、地震测定以及工厂煤量的测量。Lorensen和Cline则以立方体单元为研究对象,每个立方体由相邻两层切片上的8个数据组成。对于一个已知的等值面(其中某一变量取常数值的面)的值,立方体每个顶点处的值或大于或小于或等于该值。若顶点数据值大于或等于等值面的值,则该顶点位于等值面之上,赋值为1;否则该顶点低于等值面,赋值为0。等值面只与那些两端取不同值的边相交。通过利用Marching Cubes方法的这些特点将有利于煤场体积计算的程序设计,本文应用基于Marching cubes的煤堆显示与计算的主程序界面如图2所示,图的左边是重构的煤场曲面体图形,曲面体由有限个规则立方体和被截立方体组成,图的右边是截取的二维截面图。

图2 基于Marching cubes的煤堆显示与计算的主程序界面
2.3 三维曲面体各种体积计算方法的实现
对三维曲面体体积的计算有很多方法[3],如DTM法、单位立方体累计计算法—方格网法、基于横截面的体积计算方法—等截面法、等高线法等,考虑到三维数据场的显示与体积计算能够都兼顾到,本文主要应用的是方格网法和等截面法。
2.3.1 单位立方体累计计算方法
通过激光技术可以得到煤场的二维数据,但是要利用这些数据估算它的体积,我们可以应用单位立方体累计的计算方法—方格网法。利用Marching Cubes重构三维图形时[4],令i,j,k分别表示重构出来曲面体的x,y,z方向的不同单位序号的取值,将i,j,k与等值面相交进行比较,如果没有交点,则得到的单位立方体都是完整的,此时需将规则立方体个数k加1,特别需要注意的是在i=0或j=0或k=0时等,即移动的立方体处在外表面时,它是等值面上的一个规则立方体,此时规则立方体个数k仍需加1;在对立方体内的等值面进行三角片化时将会出现不完整立方体,此时就按照计算不规则立方体的方法计算体积。
利用立方体单元的两种对称性,可以将不规则立方体三角片分布的种类由256种情况减少到15种[2]。本文列举了其中比较常见的3种不完整立方体被截面的几何构成图,如图3所示。我们就不规则立方体的体积的计算参照如图3中的(b)[5]所示,先根据Marching cubes等值面的计算得到交点的坐标分别为C(a1,b1,c1),B(a2,b2,c2),D(a3,b3,c3),不规则立方体的体积等于规则立方体的体积减去上部被截部分,这样就可以根据体积公式算出我们所要求的不规则立方体的体积为

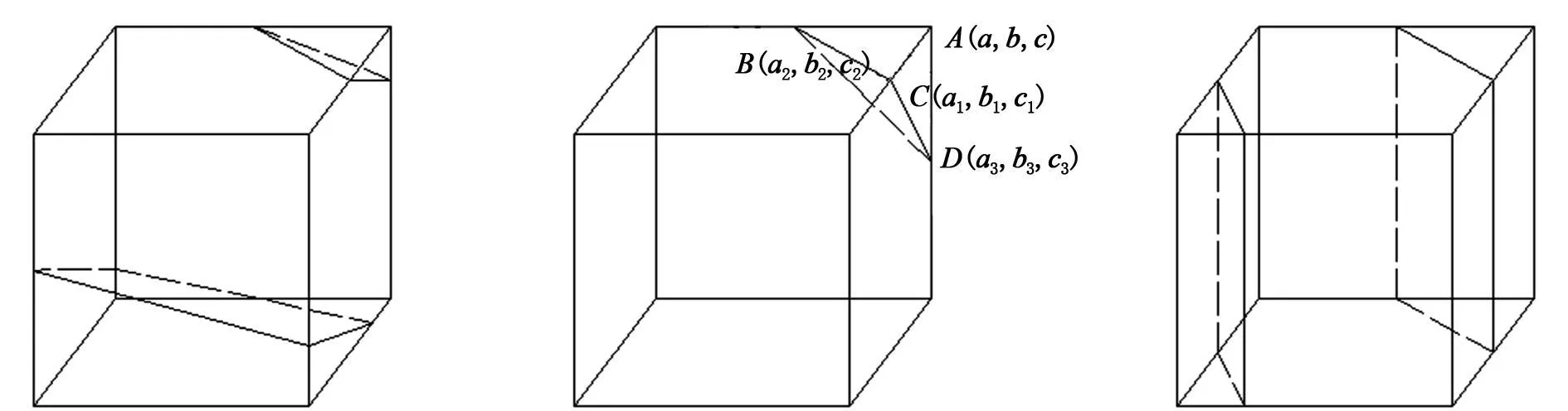
图3 被截不完整立方体构成的3种常见图形
通过上面程序设计可以算出煤场中煤的保存量,同样我们也由此得到工厂里煤的消耗量,根据每天的产电耗煤指标就可合理组织煤场煤的调度,以保证工厂有合理而经济的煤储量,实现对煤的合理管理和调用。
2.3.2 基于横截面的曲面体积计算方法
利用横截面计算煤堆的体积是另一种高效的体积计算方法,这种方法也称断面法[3]求体积。此方法首先将煤堆y轴方向的长度平均等份为n等份(n为正整数),如图4所示,且设在yi点的横截面的面积为si,在yi+L点的横截面的面积为si+1,这时当si与si+1形状相似,相对误差不大于20%,采用棱柱体体积计算公式求体积,否则采用截锥体体积计算公式,即
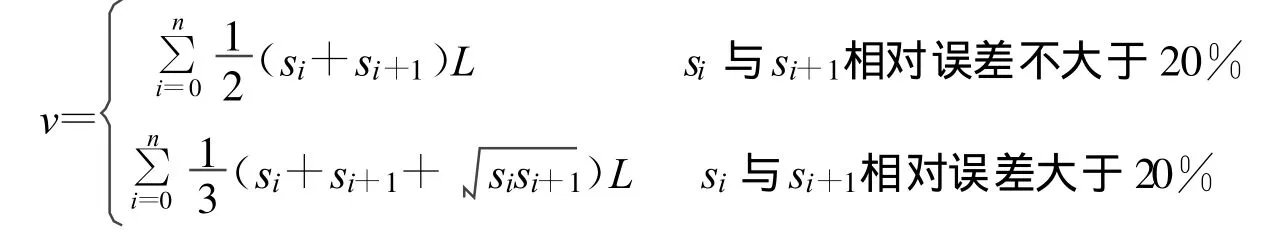
式中:v为煤堆的体积,L为相邻截面的距离,si为第i个截面的面积。
2.4 两种方法对不同种类煤的重量的计算精度的分析
据煤的煤化程度和工艺性能指标煤可以分为褐煤、烟煤、无烟煤和硬煤等,它们的比重分别为1.30×103kg◦m-3,1.28×103kg◦m-3,1.56×103kg◦m-3,1.21×103kg◦m-3,又根据经验公式可知质量 =体积×比重,即m=v×p,用上述两种方法获取三维煤堆曲面体的体积,继而求得煤堆的质量。单位立方体累计计算总体积的方法求得消耗掉煤的重量与实际消耗掉的煤重量(称量出实际用掉的煤量)相比,计算精度达到98.76%,基于横截面的曲面体积计算方法求得的重量与实际的煤重相比,计算精度达到96.47%。
3 结束语
上述2种二维体积计算方法尽管都可以计算出煤堆的体积,但是2种方法之间各有优缺点。单位立方体累计计算三维曲面体体积的方法得到煤堆的体积与实际量相比误差较小,尤其是在单位立方体的取值越小,即曲面体划分成 n×n×n,当n较大时,程序处理与计算的时间会稍长,而基于横截面计算体积的方法得到煤堆体积的时间相对而言较短,但误差会大些,这两种体积计算方法的精确度都能满足工程的要求。
利用Lase测得的截面数据并通过Marching Cubes方法重构煤场的三维图像的同时,可以同时计算得到三维数据场的体积,即利用不参加等值面构造的单位立方体累计和参加等值面构造的不完整立方体的体积累加而计算三维曲面体总体积的方法实现对三维图像体积的计算,基本上等值面构造和体积计算是并行的,程序的运行效率大大提高。因此在获取曲面体体积时,尽量采用单位立方体累计计算体积的方法。
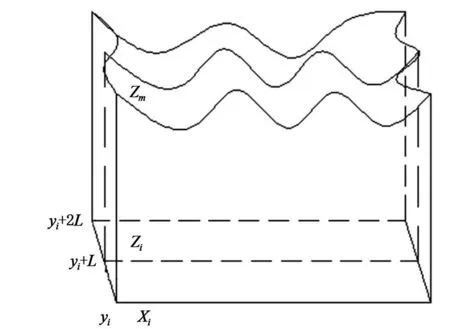
图4 二维截面组成的曲面体体积单元计算示意图
[1]蒋先刚.三维数据场重构与显示工程软件设计[M].北京:中国水利水电出版社,2009:9.
[2]DAVID R.计算机图形学的算法基础[M].石教英,彭群生,等译.北京:机械工业出版社,2006:7.
[3]廖克武,金永强.南方CASS基础矿山储量与断面法计算误差分析[J].西部探矿工程,2009,(3):187-191.
[4]程东旭.一种改进的Marching Cubes算法[A].第十二届(北京)全国图象图形学学术会议(NCIG'2005)[C].北京:清华大学出版社,2006,(4):426-431.
[5]徐毅,李晓梅,许润涛,等.对体可视化Marching Cube算法的改进[J].计算机工程,1999(11):100-105.
