用户出行费用综合更新自学习模型的研究
2010-07-05贺振欢
贺振欢
(北京交通大学轨道交通控制与安全国家重点实验室,北京100044)
He Zhenhuan
(State key Laboratory of Rail Traffic Control and Safety,Beijing Jiaotong University,Beijing 100044,China)
用户出行费用是指用户对出行过程中所付代价的一种综合评估,是用户出行过程中进行路径选择的主要依据。因此,研究和描述用户出行费用更新的机理对于路径选择等相关研究具有重要理论意义,进而也会对交通管理及ITS等相关研究产生重要影响。用户对于出行费用的判断往往要受到多方面的影响,导致其对于出行费用的估计会不断变化。为此,研究人员提出了均衡模型[1]、近期调整模型[2]、权重模型[3]等,从不同方面反映了行人对出行费用的估计及学习行为。但这些模型或多或少都存在一定的局限性,不能全面地反映出行者对于路径费用的认知和学习过程。因此,本文将综合上述各模型的优点构造新的学习模型。
1 费用估计模型
影响用户对于出行费用判断的因素很多,除当前交通流信息的影响外,用户往往还要受到以往路径选择及其走行结果的影响,其原因在于出行者会不断地从以往的出行结果中获取和更新关于路径出行费用的相关信息,并据此调整路径费用的判断[1-4]。此外,路网的固定信息(如路径长度及自由流速度)也是影响路径费用的重要因素。因此,出行者对路径出行费用的估计要受到当前车流信息、出行经验信息和固定信息3个方面信息的影响。路径是由若干路网单元(包括路段和交叉口)组成,因此可将路径费用分解为若干路网单元的费用。出行者j对路网单元a当前费用的估计模型可描述为
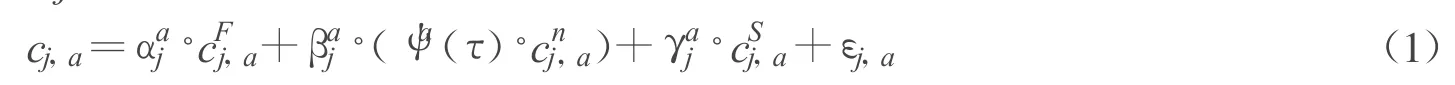
根据路径选择的依据不同,路网中出行者一般可分为3类:临时型、经验型和固定型。模型中个参数标识出了出行者j路径选择过程中对各种信息的依赖程度,调整3个参数的大小即可使模型满足对不同类型的出行者进行描述的要求。当时,模型描述的是临时出行者的费用估计行为,该类出行者主要依赖当前路网车流信息做出行决策;当时,模型则转变为完全经验型出行者的出行决策行为描述,这类出行者对路网每日的车流情况非常熟悉,主要依据长时间积累的出行经验进行路径费用的估计;而当时,模型又变为对完全固定型出行者的决策描述,该类出行者对路网极不熟悉,只能依靠从地图上获取的静态信息进行出行决策。
2 出行费用自学习原理分析
现有的自学习模型主要描述经验费用的学习过程,实际上出行者随着经验的增加,出行者在费用估计时对各种信息的信赖程度也在不断变化之中,即αaj,βaj,γaj也不断变化之中。因此,本文提出综合更新自学习模型,以当前费用估计为核心,将出行者的费用估计和学习过程分为当前费用估计、经验费用学习和权重调整3个部分[2,5,6],并建立相应模型。当前费用估计模型主要用于将经验费用与当前车流分布等实时信息以及部分固定信息相结合,产生新的估计费用。权重调整模型主要是根据出行者对网络的熟悉程度不同而调整各项信息在当前费用估计时所占的比重。经验费用更新模型主要描述用户每日估计费用的变化规律。该模型综合了历次出行经验对用户出行费用预测的影响,并以权重调整模型为基础对路径经验费用进行滚动式更新。
上述3个模型并不是完全独立的,而是互为基础、互相影响。首先,出行者在出发前估计当前费用,并据此选择合适的出行路径;其次,随着出行次数的增加,出行者对网络熟悉程度的增加,费用预测模型中的权重参数要发生变化;同时,出行结束后,出行者要根据本次出行的实际费用对出行经验值进一步更新。整个过程如图1所示。
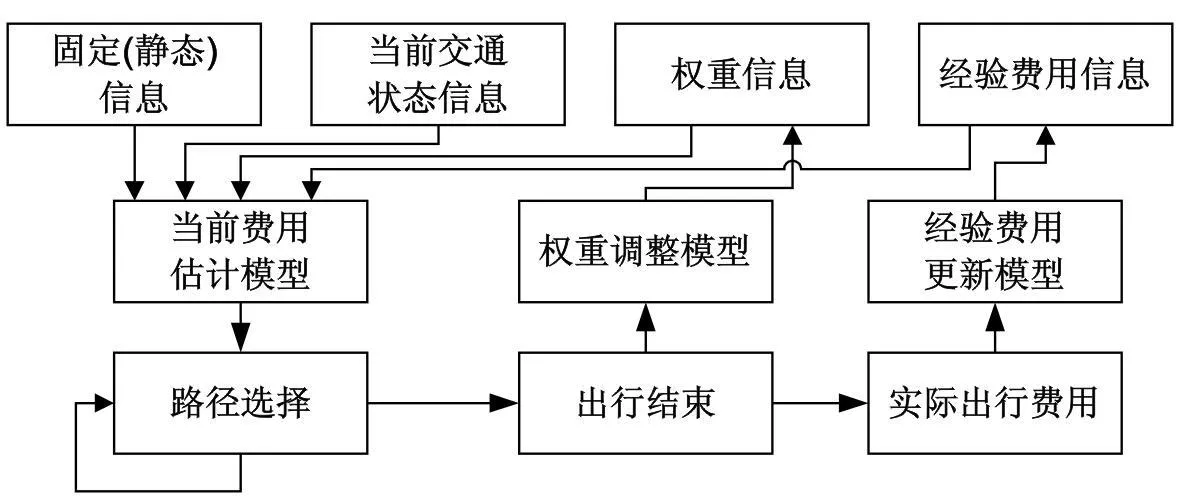
图1 基于自学习的费用估计过程
当前费用估计模型包含了同时影响出行者当前费用估计的3种信息,而这些信息进一步又可归为两类:实时费用信息和非实时费用信息(包括经验信息和静态信息)。实时费用信息系数的值主要与出行者个人习惯及其受诱导系统的影响的程度有关,可令其中M为根据个人特性而确定的常数。在无诱导系统的情况下,出行者只能根据所处路网单元的车流状况大致推断路网中当前车流信息,所获信息的准确度较低,对该信息的信赖程度也很小。
3 调整模型
3.1 权重调整模型
在实际出行过程中,随着出行者经验的增加,对经验费用的信赖程度也在不断变化,使权重也相应发生改变。一般出行过程中途经路网单元a次数越多,出行者对其熟悉程度就越高,也就越信赖于经验值进行费用估计,相应地值就越大而的值越小,反之亦然。若出行者未受到诱导系统的影响,当其对路网单元a的选择次数n=0时,出行者无任何经验,此时道路费用估计主要信赖于固定信息,因此随着出行次数的增加,出行者经验增加,使出行者在费用估计过程中对固定信息的信赖程度迅速降低,因而值迅速下降,而同时值迅速上升。但随着出行次数的进一步增加,若路网及交通管制措施未发生较大变化,则出行者的经验值会逐渐接近于实际情况,变化较小,此时值会相应逐渐趋于稳定,特别是当权重随出行次数的变化特征如图2中曲线a,b所示。
本文尝试用负指数函数来拟合权重 γaj随路网单元被选择次数而变化的过程,即
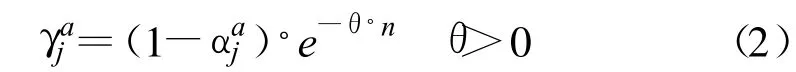
由于不同城市路网车流状况的稳定性及出行者个人特性等原因,不同的出行者的权重变化曲线会有所不同。因此,模型提出了调节系数 θ,用于调节出行者权重变化的速度,该值需通过对不同城市或不同类型出行者调查统计后确定。
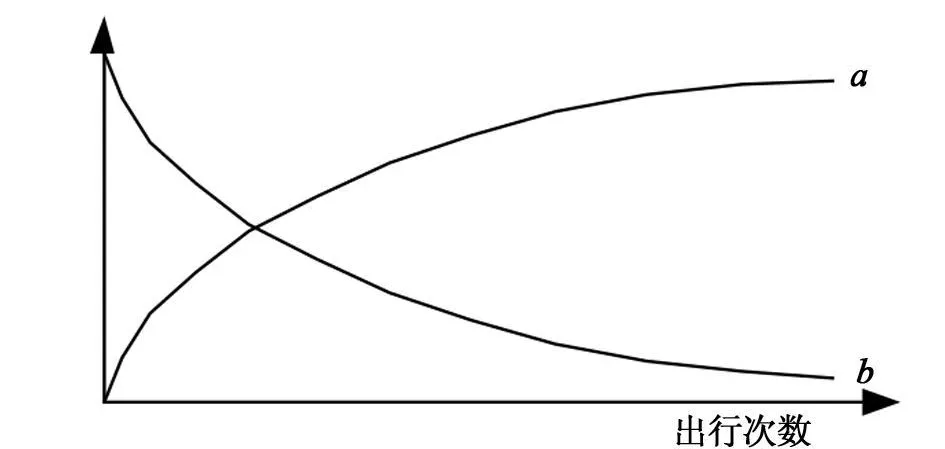
图2 费用估计系数变化曲线
另外,历史车流信息是有一定有效期的,出行者只会被最近一定时间内的信息所影响。因此,模型2中的参数 n实际上应为最近D天内出行者选择单元a的次数。这样,实际上并不是单调递减或递增的,而是会随着出行者选择行为变化大小。
综上所述,可得3种权重的变化调节模型为

3.2 费用调整模型
每一次出行结束后,出行者都要根据本次出行的实际情况更新其经验费用,本文将综合目前较为常用的权重模型和近期调整模型的优点,采用预测时间与实际走行时间的偏差对费用经验值进行修正,同时利用权重模型能有效反映出行者不断学习、调整认识的连续过程这一特性构造新的费用学习更新模型。由于出行者的经验值与此次出行之前的经验值相关,同时会按本次出行延误时间对经验值进行调节。因此,出行后的经验值更新模型可描述为
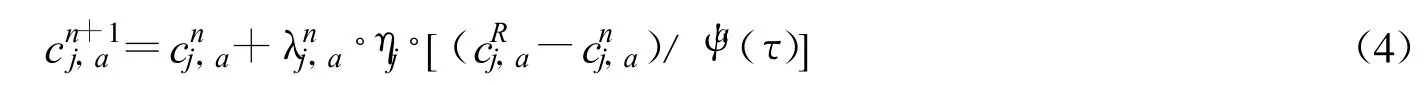
其它参数同前。
上述3个模型通过出行前的经验学习及融合、出行后经验更新以及权重调整几个过程,比较完整地描述了道路估计费用的演变,从而更加完整、准确地反映了出行者的对路径费用的学习和更新过程。
4 综合学习模型
上述自学习模型描述了出行者对任一路网单元进行学习的过程。实际上,由于城市路网规模巨大,出行者不可能对路网中所有的单元都逐一学习并获取经验值。通常,出行者只能记住那些最近一段时间内经常发生拥挤的路网单元的历史信息。若用表示路网单元a在出行者j最近第n天途经时是否发生拥挤(在本文研究中,“拥挤”主要参考HCM手册中服务水平定义,服务水平为E级以下为拥挤),1表示发生拥挤,0表示没有,则出行者j历史经验学习对象集合可表示为
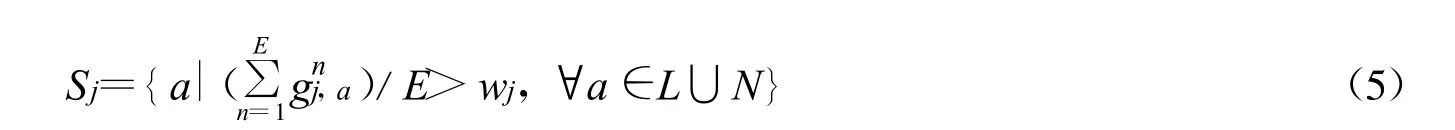
式中:E为出行者学习时效长度,即多少天以内的经验对用户是有效的;wj为出行者j的学习标准,只有某路网单元拥挤频率达到这个标准后,出行者才会开始相应历史费用的学习;L和N分别为路段和交叉口集合。
因此,可将经验值更新模型(式4)改进为
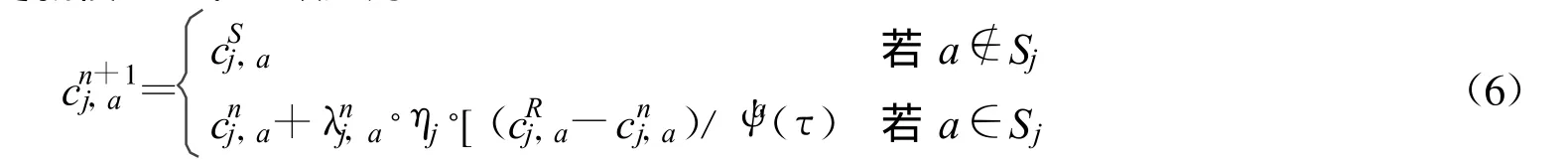
同样,权重调节模型(式3)实际上也是相对于集合Sj中的单元而进行的,而对于∀a∉Sj,出行者进行费用估计时基本不会考虑经验费用,则此时该模型应描述为

上述学习过程是针对每个出行者而言,这样系统需要建立每一个出行者的出行费用及权重系数矩阵,当系统中出行者较多时,这种方式显然不太可行的。因此需要对学习过程进一步简化:将路网划分为若干OD小区,将从同一个小区出发到另外同一个小区的出行者归结为一类,对每一类分别进行自学习过程。该简化方法主要出于如下考虑:首先,相同类别的出行者出行过程中所经过的区域有很大一部分应该是相重合的;其次,对于出行历史时间影响较大的是拥挤现象,而拥挤现象通常会在一定范围内传播,即使出行者在当日出行中未选择拥挤路网单元,也会对一定区域内的拥挤状况有所了解。因此,对于同一类的出行者来说,其出行经验会大致相同,可近似地用同一个经验值及权重系数来表示。这种处理方式在保证一定精度的同时又能大大简化实际处理过程。
按上述方法进行自学习时,具体的小区划分方法及出行者分类精度应根据模拟实验要求及实验条件来确定。而每一类的当日出行费用值则可由该类中每一个出行者的出行费用转化为高峰时段费用后取平均值。
5 算例
根据上述模型,相应的仿真系统已被开发,并对4×4路网进行了仿真研究。仿真过程中,行人的路径选择主要采用Logit模型,并直接采用走行时间作为出行费用。仿真过程中,用户学习率统一设为25%;θ取0.1以保证约30日后相关路径的费用估计主要由经验费用和实时费用来决定;M取0.2。仿真过程中某路段的实际平均走行时间与经验估计时间变化如图3所示。
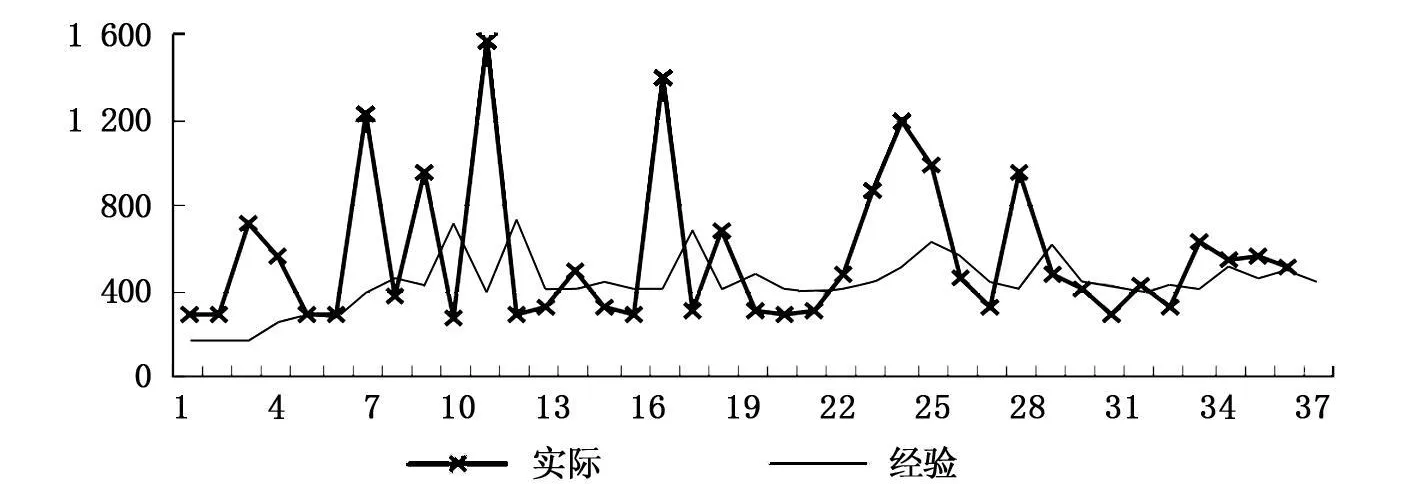
图3 某路段实际走行及经验时间变化图
从图3可以看出,经过一段时间学习后,路段经验费用的变化趋于平稳,并与整个路段的实际平均费用相接近。同时,整个路段的实际平均走行费用变化幅度也相应缩小,说明用户经过学习后,能较真实地评估走行费用,使路网中用户的出行分布更加均衡。
6 小结
提出了出行费用估计的综合更新自学习模型,将当前费用估计归结为实时费用、经验费用以及固定费用3种信息共同作用的结果。在描述经验费用自学习过程的同时,提出上述3种费用的权重也在不断学习变化之中,并提出相应权重调整模型。上述3种模型集出行前的费用估计、出行后经验更新以及权重调整几个过程为一体,形成比较完整的路径费用学习演变过程。
[1]HOROWITZ J L.The stability of stochastic equilibrium in a two-link transportation network[J].Transportation Research Part B,1984,18(1):13-28.
[2]HANI S M,CHANG G L.Experiments with departure time choice dynamics of urban commuters[J].Transportation Research Part B:Methodological,1986,20(4):297-320.
[3]RICHARD HM,EMMERINK,et al.The potential of information provision in a simulated road transport network with non-recurrent congestion[J].Transportation Research Part C,1995,3(5):293-309.
[4]MOSHE B A,ANDRE D P,ISAM K.Dynamic network models and driver information systems[J].Transportation Research Part A,General,1991,25(5):251-266.
[5]ZHOU X S,HANI SM,ZHANG K L.Dynamic micro-assignment modeling approach for integratedmultimodal urban corridor management[J].Transportation Research Part C,Emerging Technologies,2008,16(2):167-186.
[6]曲卫民.交通流模拟体系中用户出行路径选择模型的探讨[J].北方交通大学学报,2004(3):44-4.
