多阶段复合型遗传算法的结构及性能研究

刘立民,潘 伟,庞彦军,李法朝

(1.河北工程大学 理学院,河北邯郸 056038;2.河北科技大学 经济管理学院,河北石家庄050018)

遗传算法[1]是由美国控制论专家Holland提出的一种基于生物进化论及孟代尔基因遗传理论的搜索型优化算法,是近年来在数据挖掘、优化控制、人工智能、专家系统等领域的一个热点研究内容[2-4],并且在函数优化、机器学习、人工神经网络、分子生物学和优化调度等领域得到了广泛应用。

尽管遗传算法思路直观、操作简单,但却常常存在“未成熟”收敛以及收敛精度不高等方面的不足,尤其对大范围、高精度的优化问题往往不能收敛到全局最优解。近年来,人们提出许多改进的遗传算法,但大多是集中在选择、交叉和变异概率及适应度函数的选取上[5-6],且均具有较强的针对性,没有从根本上解决上述算法的不足。针对上述不足,结合遗传算法的求解机理,提出了多阶段复合型遗传算法,并利用Markov链理论和仿真技术进行算法的收敛性能分析,为复杂系统数值优化等方面的优化问题提供了依据。

1 MSC-GA的结构

1.1 问题的提出

现实生活中无论是复杂优化系统还是其他领域的优化问题,对精度的研究具有很高的应用价值。理论上,当所考虑的优化问题存在最优解时便一定能够求出精确的值,但在实际问题中,由于模型的提炼过程存在理论误差、数据的欠缺存在信息误差、认知观念的不同存在认识偏差等等,因而常常考虑的是优化问题的满意解。从直观的角度来看,优化问题变量变化范围与解的精度具有密切的联系,当优化变量的变化范围较大时,便很难求出精度较高的满意解,而当变化范围很小时,则易于求出精度较高的满意解。因此,对寻优范围大、精度要求高的优化问题,若能够按照某种策略,在不损失最优解的情况下逐步缩小问题的寻优范围,那么对求得精度较高的满意解显然是有利的。

基于以上观点,提出了多阶段复合型遗传算法(简记为MSC-GA),过程分为最优预判和最优搜索两个阶段。最优预判阶段由几段相互独立的遗传搜索构成,其目的是以各次所得的相对满意解为基础,通过某种策略确定问题最优解或满意解的基本特征,进而结合某种方法(比如统计规律、网格理论等)缩小寻优范围;最优搜索阶段是以最优预判的结果(即缩小后的寻优范围)为基础,继续进行精度更高的遗传搜索。为了更形象和直观地体现MSC-GA的结构,将之记为(K⊕1)-GA,其中k表示最优预判部分重复执行的次数,1表示最优搜索部分。显然,k=0时,(K⊕1)-GA即为现行的基本遗传算法SGA,这表明(K⊕1)-GA是SGA的推广和完善。下面给出(K⊕1)-GA的具体实施策略。

1.2 实施步骤

按照上面的分析和讨论,我们可以遵循下面的步骤来设计(K⊕1)-GA。

Step1选择个体的编码形式。

Step2(最优预判)独立地重复k次如下操作:随机产生N个个体构成初始种群,并对其进行指定代数的遗传进化操作,记录各次进化结果中的个体及其对应的适应度。

Step3(缩小搜索范围)利用Step2所得的结果,按照某种原则确定相对满意解集合,并结合解的编码形式缩小寻优范围。

Step4(最优搜索)以Step3所得的范围为基础,进行最后阶段的遗传搜索。

Step5(终止条件检测)若满足终止条件,则输出当前解;若不满足,则以Step4搜索后所得的范围为基础,转到Step2。

2 缩小搜索范围的策略

缩小搜索范围是(K⊕1)-GA的核心环节,在实际实施过程中,应结合优化问题的性质以及编码的形式来确定具体的方法。就一般情形而言,可以概括为下面的两种方法:

方法I.对于二进制和符号形式的编码,可通过确定重要或非重要基因位的策略缩小寻优范围。

方法II.对于实数编码,可通过缩短区位的途径缩小搜索区域。

针对(K⊕1)-GA在最优预判阶段所得到的K◦N个个体,采用如下流程图来缩小搜索范围:

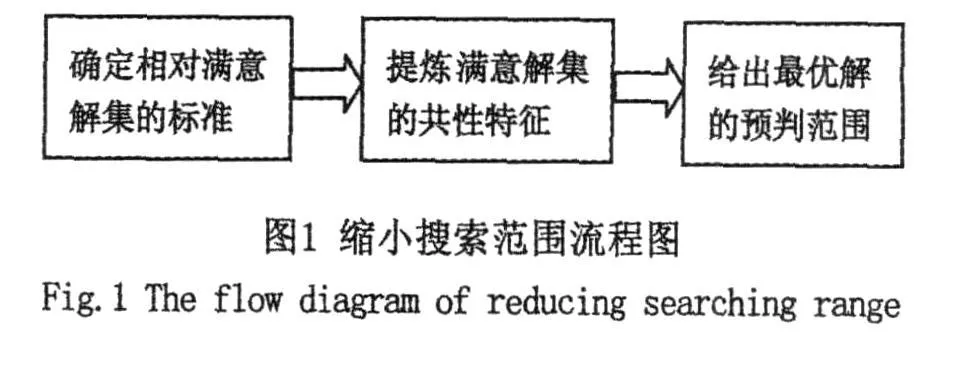
下面给出几种具体的缩小搜索范围的方法。

2.1 基于统计规律的缩小范围方法

利用统计理论可知,只有当数据充分多的时候,所得的统计规律才具有可靠性,因而,当最优预判阶段的重复循环次数K较大且所得到的K◦N个个体具备一定的共性特征时,可以按照如下策略来缩小寻优范围:

1)确定相对满意解集C

方法1按一定的比例α(0＜α≤1)确定,即选择int(K◦N)个适应度较大的个体作为相对满意解集C。

方法2以K◦N个个体的最大适应度W为标准,通过相对最优满意度 β(0＜β＜1)来确定相对满意解集,即选择K◦N个个体中的适应度w满足(W-w)／W≤β的个体构成相对满意解集C。

2)给出最优解的预判范围

方法1通过基因位稳定率来确定重要基因位,即选择满意解集C中个体的基因稳定率超过β(0＜β≤1)的基因位作为重要基因位。该方法适应于非实数编码的情形。

方法2利用对称分位的方式确定预判范围,即以满意解集的概率分布(直方图)为基础,通过分布的双侧 β(0＜β≤1)分位点来确定最优解的预判范围。

2.2 (K⊕1)-GA的实施步骤

当预判阶段所得到的K◦N个个体不存在不明显的共性特征时,利用统计规律便不能得到可靠程度较高的缩小范围,为了尽可能地不损失最优解的信息,且达到缩小寻优范围的目的,我们按如下步骤,采用Min-Max策略来缩小寻优范围:

步骤1按照某种规则(如:按一定的比例去掉较差的个体;按照相对满意度去掉较差的个体,等)得到相对满意解集C。

步骤2以相对满意解集C为基础,取其中适应度最小的个体及适应度最大的个体作为最优预判范围的下限和上限。

2.3 几点注明

1)最优预判是为了在不损失最优解的前提下逐步的缩小优化问题的寻优范围,因此,为了获得尽可能多的最优解的信息,在遗传操作过程中应采用最优个体保留策略。

2)K的选择直接影响到(K⊕1)-GA性能,若太大,则可能导致计算的时效性差,若太小,则可能导致最优预判结果失真。因而,在具体问题中应结合解的编码形式、预判阶段的种群规模以及所选用的缩小范围的策略来系统地确定K的取值,一般而言,对于基于统计规律的范围缩小方法,K的取值不易太小,应在4-10之间为好;而对于基于Min-Max的范围缩小方法,K的取值不易太大,在3-6之间为好。

3)最优预判阶段和最优搜索阶段的的目标和作用是不同的,因而,相应的遗传参数设置可以是不同的。一般来说,最优预判阶段的变异概率应适当大于最优搜索阶段的变异概率,而最优预判阶段的进化代数要小于最优搜索阶段的进化代数。

3 (K⊕1)-GA的收敛性分析

在遗传算法的搜索过程中,由于第t+1代种群X(t+1)只与第t代种群X(t)有关,且各种群之间的转移概率与时间的起点无关,因而遗传算法的遗传序列是一个齐次的Markov链。本部分的主要工作是利用Markov链理论来分析(K⊕1)-GA的收敛性[7]。

定义1[8]设 X(t)={X1(t),X2(t),…,XN(t)}为遗传算法的第t代种群(t))表示种群X(t)的最优适应值,f*=max{f(X)｜X∈S}表示全局最优值。若则称遗传序列是收敛的。

定义2[9]设为Markov链从状态i出发经过n步首次到达状态j的概率:1)若对任意状态 i,j,均存在自然数m使得则称是不可约的;2)若对任意状态i,j,D={n:n≥0}非空且D的最大公约数为1,则称{X(t)}是为非周期的;3)对于状态j,若=1,则称状态 j是常返的;若称状态j是非常返的。

定义3[9]对于Markov链{X(t)的常返状态,若则称 i为正常返的;若状态空间中任何状态都是正常返且非周期的,则称为遍历的。

定理1(K⊕1)-GA收敛到最优解的概率小于1。

定理2采用最优个体保留策略的(K⊕1)-GA的遗传序列{X(t)依概率1收敛于全局最优解。

4 实例仿真

为了进一步分析(K⊕1)-GA的特点和收敛性能,本部分结合一个具有相当复杂度且最常用的测试算法性能的函数进行分析和讨论。

例考虑Shaffer函数[10-11]:

该函数在定义域内只有一个全局最大值点(0,0),最大值为f(0,0)=1。

下面采用二进制编码和实数编码,利用SGA和(K⊕1)-GA分别对问题进行寻优处理。其中,各参数设置如下:

1)采用二进制编码

基本遗传算法:种群大小80,进化最大代数100,交叉概率pc=0.6,变异概率 pm=0.002,迭代结果如图2所示。

(K⊕1)-GA:①最优预判阶段:种群大小40,进化最大代数100,交叉概率pc=0.6,变异概率pm=0.002;预判次数 k=5,②最优搜索阶段:种群大小80,进化最大代数100,交叉概率 pc=0.6,变异概率pm=0.001;③缩小搜索范围的策略采用寻找重要基因位,以预判阶段所得满意解集为依据缩小寻优范围,迭代结果如图3、图4、图5所示。

2)采用实数编码

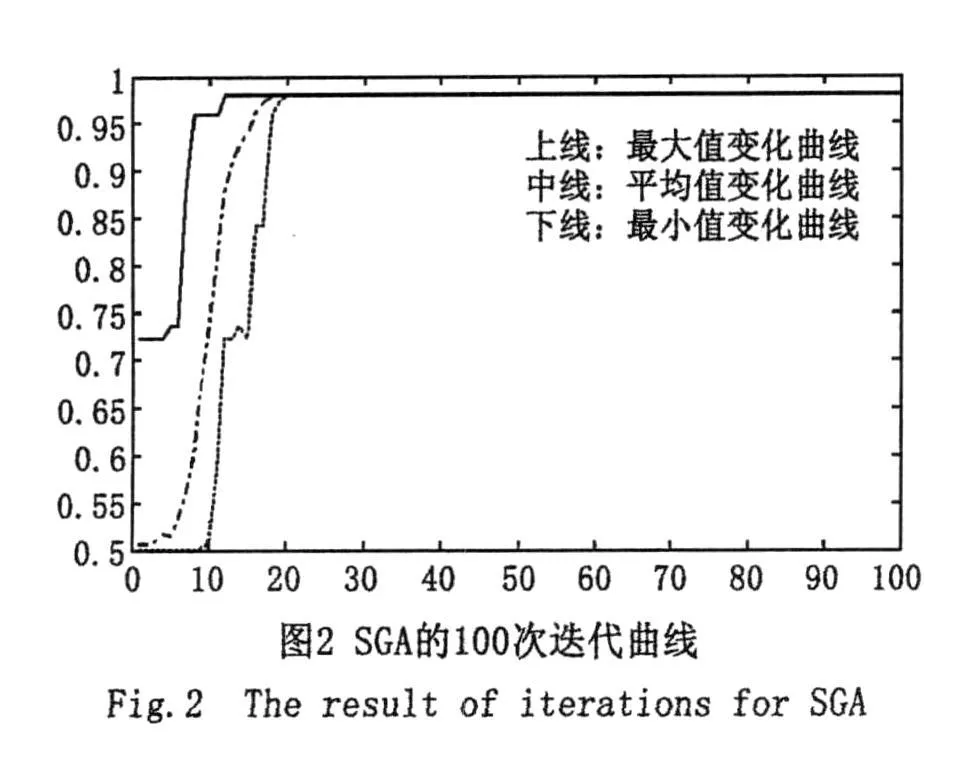
基本遗传算法:种群大小80,进化最大代数100,交叉概率 pc=0.6,变异概率pm=0.002,迭代结果如图6所示。

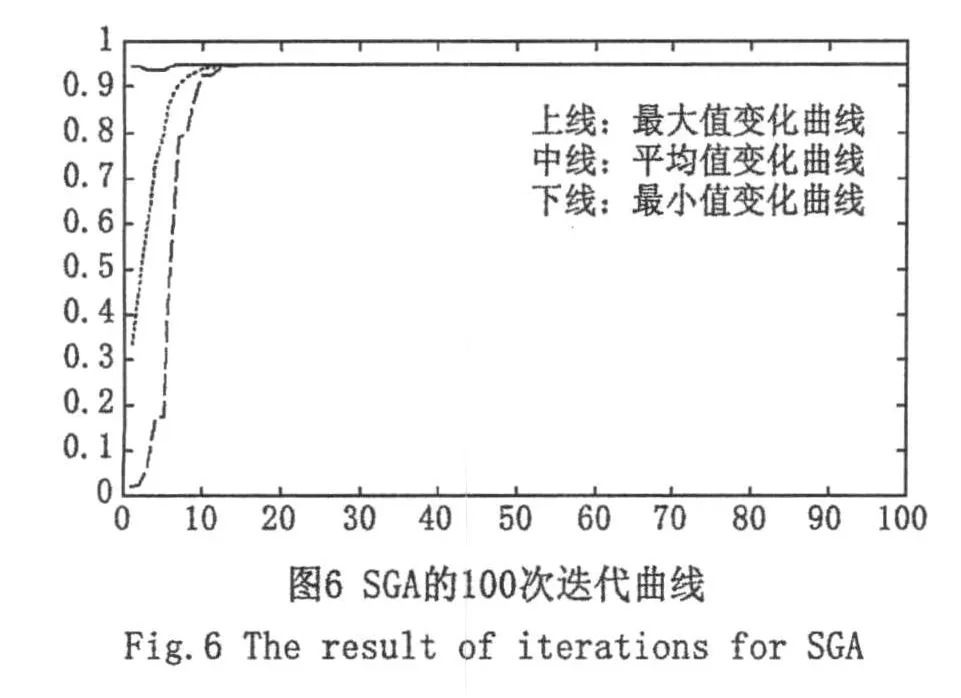
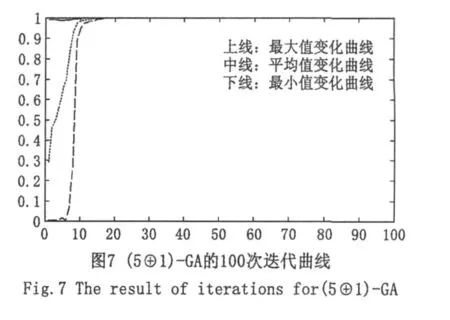
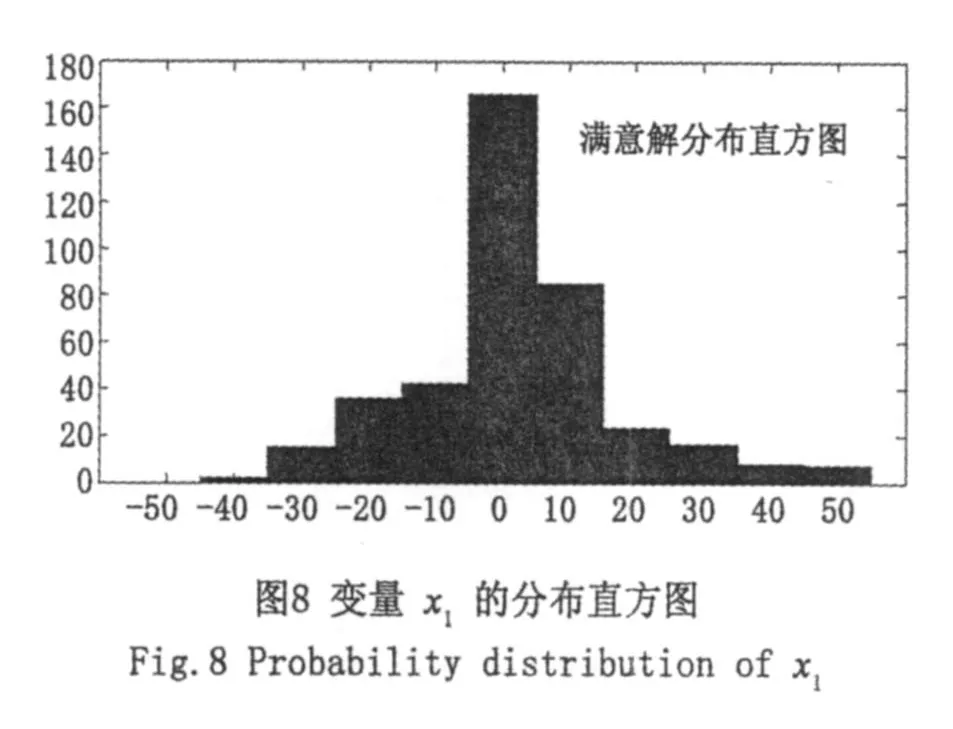
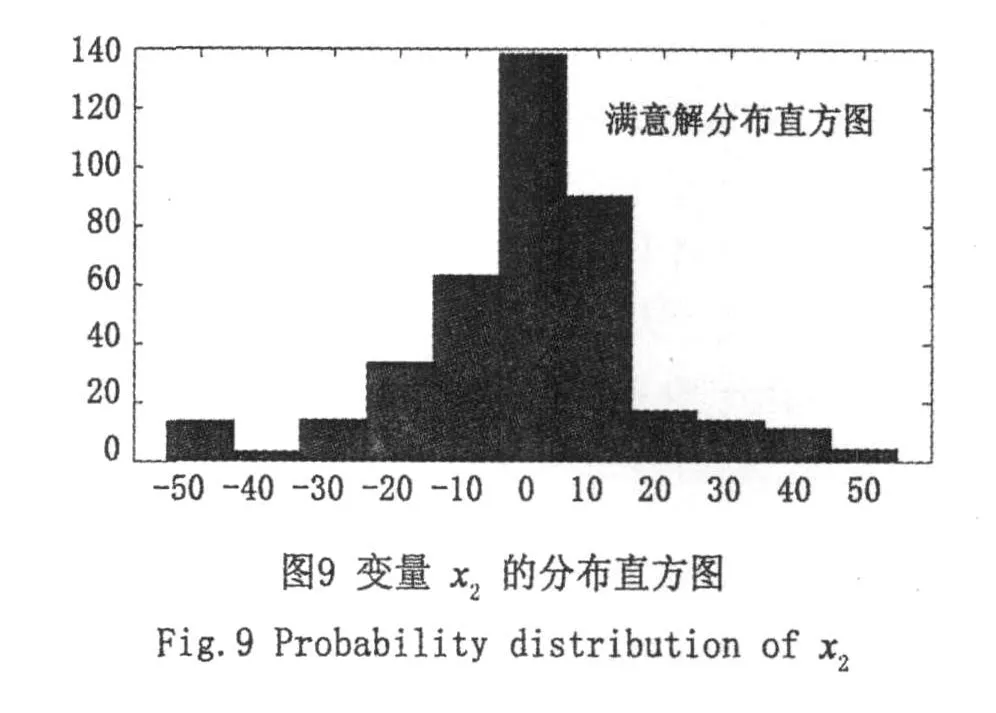
(K⊕1)-GA:①最优预判阶段:种群大小80,进化最大代数100,交叉概率pc=0.6,变异概率pm=0.002;预判次数K=5;②最优搜索阶段:种群大小80,进化最大代数100,交叉概率pc=0.6,变异概率pm=0.001;③缩小搜索范围的策略是以预判满意解集的概率分布(直方图)为依据,通过分布的双侧β(β=0.1)分位点来缩小寻优范围,其迭代结果如图7、图8和图9所示。

图2和图3、图6和图7分别表示采用二进制编码和实数编码的SGA和(5⊕1)-GA的100代进化曲线图(其中横坐标表示迭代次数,纵坐标表示目标函数值);图4和图5、图8和图9为采用二进制编码和实数编码的(5⊕1)-GA在预判阶段所得满意解的分布直方图。

自图2和图6可以看出,无论采用二进制编码还是实数编码,基本遗传算法始终不能收敛到精度较高的满意解;而自图3和图7可知,无论采用哪种编码,(5⊕1)-GA算法均能很好地收敛到全局满意解。这表明-GA在收敛精度上较基本算法有很大提高。自图4和图5,图8和图9可以看出,采用二进制编码和实数编码时在预判阶段所得的满意解以较大的概率落在优化变量的全局最优解附近,这表明第2部分提出的缩小寻优范围的策略是可行的。

为了进一步分析(K⊕1)-GA的收敛性能,针对上述参数设置,分别就二进制编码和实数编码进行了10次独立的求解试验,结果如表1,其中所采用的缩小范围的策略分别为:

二进制编码:利用预判满意解集,通过寻找重要基因位来缩小寻优范围。

实数编码:以预判满意解集的概率分布(直方图)为依据,通过分布的双侧β(β=0.1)分位点来缩小寻优范围。

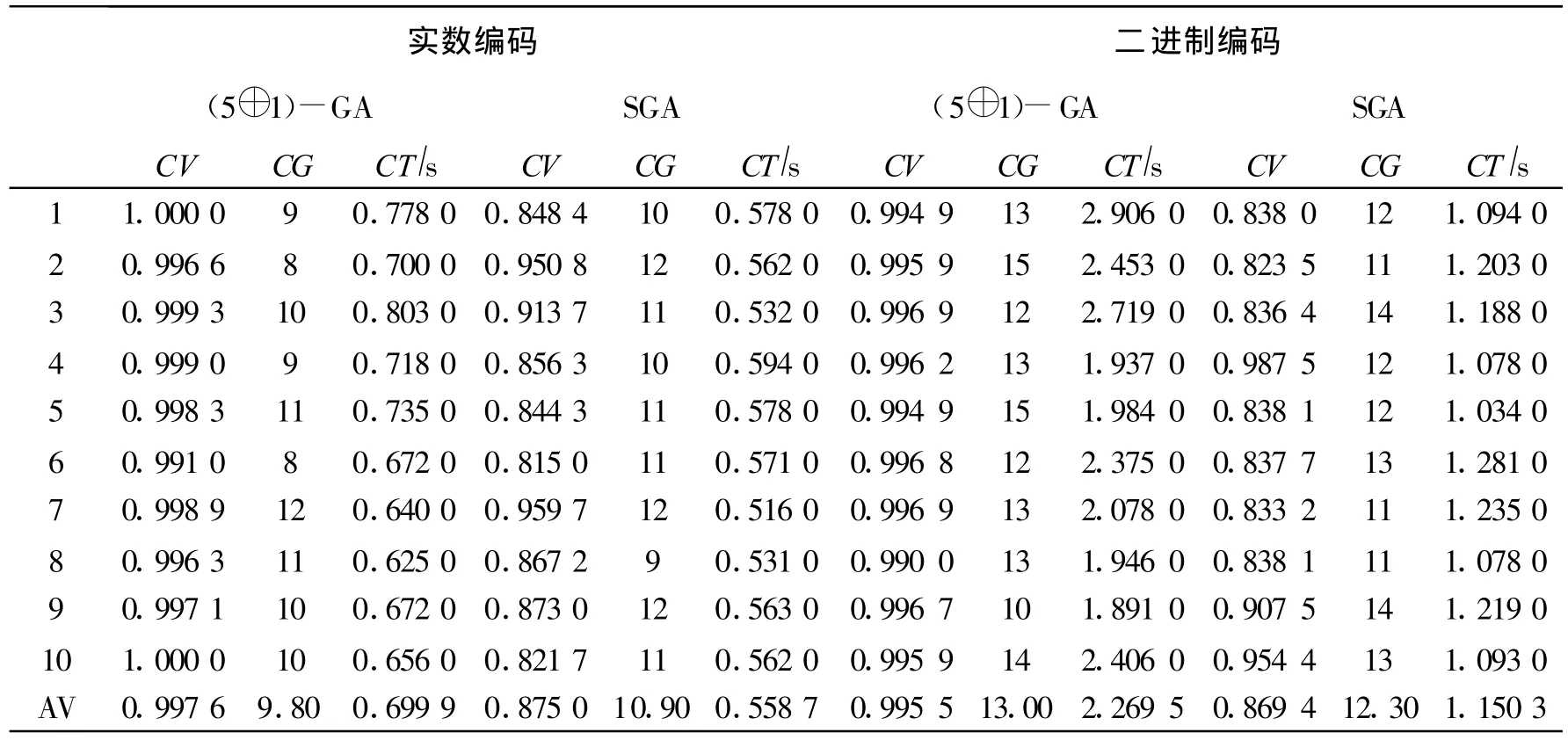
表1 二进制编码和实数编码的收敛结果对比表Tab.1 The comparison of convergence results between binary coding and real coding

由表1可知以看出:1)无论是采用二进制编码还是实数编码,(5⊕1)-GA均具有稳定的全局收敛性能;2)采用实数编码的(5⊕1)-GA在收敛代数、收敛时间上明显比采用二进制编码的(5⊕1)-GA要低。因而,对于多变量、大范围的、高精度的连续型优化问题,采用(5⊕1)-GA以及实数编码可以达到较好的优化效果。

5 结论

针对基本遗传算法在进化过程中存在的“早熟”现象以及收敛解精度低等方面的缺点,提出了一种改进的遗传算法-多阶段复合型遗传算法,该算法的基本思想是首先寻找问题的满意解群体,然后以得到的满意解群体为基准,按照某种策略缩小寻优范围,并继续搜索精度更高的全局最优解或满意解。理论分析和仿真技术表明,该算法不仅具有良好的结构和可操作性,而且在计算效率和收敛稳定性方面均明显优于常规的遗传算法,为进一步构建复合优化方法奠定了基础,在一定程度上推广和丰富了现有的智能优化理论和方法。

[1]SRINIVAS M,PATNAIK M.Genetic algorithm:A survey[J].IEEE Computer,1994,27(6):17-26.

[2]FOGE D B.An introduction to simulatedevolutionary optimization[J].IEEE Trans,on SMC,1999,24(1):3-14.

[3]ATMAR W.Noteson the simulation of evolution[J].IEEE Trans,on SMC,1994,24(1):130-147.

[4]HOLLAND J H.Adaptation in nature and artificial systems[M].USA:Univ.of Michigan,1975.

[5]巩敦卫,孙小燕,郭西进.一种新的优胜劣态遗传算法[J].控制与决策,2002(6):908-912.

[6]韩万林.遗传算法的改进[J].中国矿业大学学报,2001(1):102-105.

[7]刘立民,马丽涛,庞彦军,等.基于多保留策略的复合型遗传算法及其收效性分析[J].河北工程大学学报(自然科学版),2010,27(1):103-108.

[8]夏道行,吴卓人,严绍宗,等.实变函数与泛函分析[M].北京:高等教育出版社,1979.

[9]方兆本,缪柏其.随机过程[M].合肥:中国科学技术大学出版社,1993.

[10]盛骤.概率论与数理统计[M].北京:高等教育出版社,1989.

[11]王小平,曹立明.遗传算法理论、应用与软件实现[M].西安:西安交通大学出版社,2002.