处理滴定分析中几个问题的体会

2010-07-02王丰

大学化学 2010年1期

关键词：弱酸酸碱常数

王丰

(新疆大学化学化工学院新疆乌鲁木齐830046)

处理滴定分析中几个问题的体会

王丰

(新疆大学化学化工学院新疆乌鲁木齐830046)

介绍应用简单酸碱体系扩展、广义酸碱平衡、广义络合效应和查漏补缺等方法处理滴定分析理论中平衡体系组分分布、副反应系数和综合性习题解析等问题的体会。

滴定分析是分析化学课程的主要内容，是以酸碱、络合、氧化还原和沉淀四大化学平衡为基础，滴定方法为手段，物质之间的化学计量关系为依据的实现物质定量分析的一系列知识体系的总和。这部分内容涉及到的知识点较多，要求学生熟练掌握基本理论，并将其灵活应用于大量的计算过程。不少学生觉得这部分内容概念多，计算繁，在解决一些实际问题特别是综合性较强的问题时不能从容应对。其实，在滴定分析知识体系中，各种方法的理论及应用之间有着紧密的联系，在学习过程中如果能总结出它们的内在联系，并把握其特点，许多问题就会迎刃而解。在此，笔者谈谈滴定分析中处理平衡体系组分分布、副反应系数和解决综合性习题的体会，旨在为提高学生的综合理解和解题能力提供参考。

1 平衡体系中组分分布问题

正确处理平衡体系中组分分布问题是准确判断体系组成的基础，同时能为相关的计算提供依据。该问题在酸碱和络合平衡中较常见。通常我们会遇到这样的问题:判断某酸度(某络合剂的平衡浓度)下，平衡体系中各组分的分布或确定满足一定平衡分布的酸度(某络合剂的平衡浓度)。例如，用强碱滴定某弱酸HA，随着滴定剂的加入，平衡体系的组成发生相应的变化，其过程为弱酸体系(HA)→缓冲体系(HA+A)→弱碱体系(A)→强碱、弱碱混合体系(A +OH－)。以此为依据，可计算滴定过程中不同酸碱体系的pH，绘制滴定曲线;若已知溶液的酸度，也能计算出平衡体系的组成。

以下是对复杂酸碱和络合体系平衡处理的方法。

1.1 扩展简单弱酸碱体系法处理多元酸碱体系

解决简单酸碱体系中组分分布问题并不复杂，只要利用平衡计算得到组分分布分数(δ)与pH关系即可。现行教材对一元弱酸和二元弱酸体系中各有关存在形式的分布与pH的关系已做了详细的讲解。而在具体的应用过程中，会遇到更复杂的多元弱酸碱体系，可将教材上的知识加以扩展应用于这些复杂体系。具体内容如下:

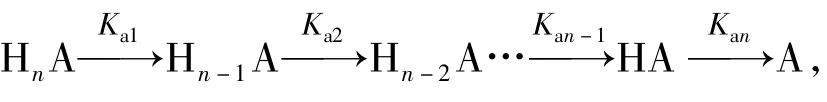
(1)体系的组成与pH关系以p Ka1，p Ka2，…，p Kai，…，p Kan－1，p Kan为界，分为n+1种情况:

pH＜p Ka1，体系以HnA为主;

p Ka1＜pH＜p Ka2，体系以Hn－1A为主;

┇

p Kan－1＜pH＜p Kan，体系以HA为主;

pH＞p Kan，体系以A为主。

(2)当体系为某单一组分时，体系的pH应该等于与该组分相关的两级相邻p Ka的平均值。例如:对以上多元弱酸平衡，pH=(p K+p K)时，体系可认为是H A单一组分。a1a2n－1

(3)若pH=p Kai，则体系中以p Kai为界的相邻两组分的分布分数相同。例如:当pH= p Ka2时，δHn－1A=δHn－2A=0.5。

利用以上结果，可以方便地解决常见多元酸的平衡问题。

例题:已知H3PO4的p Ka1=2.22，p Ka2=7.20，p Ka3=12.36，调节磷酸盐溶液的pH至6.0时，其各有关存在形式浓度间的关系是:

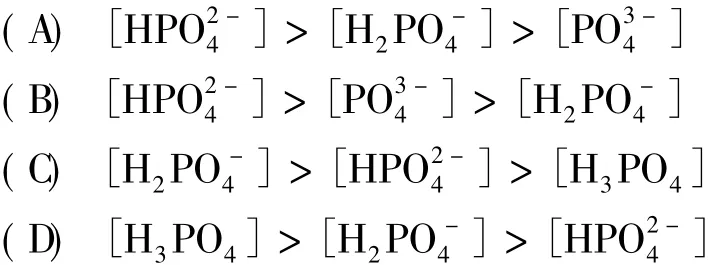
因为p Ka1(2.22)＜pH(6.0)＜p Ka2(7.20)，H3PO4在该体系主要以一级电离为主，产物为H2PO，按以上原理，pH=2.22时，［H3PO4］=［H2PO］;pH=7.20时，［HPO］=［H2PO］。与p Ka1(2.22)相比，pH=6.0更接近于p Ka2(7.20)，说明一级电离较二级电离完全，故答案(C)正确。

多元弱碱体系(An－)的平衡是其相应弱酸(HnA)平衡的逆过程，只要将其各级碱常数Kbi换算成其共轭酸的酸常数(Ka=Kw/Kb)后，即可按相应的多元弱酸体系处理。

1.2 广义酸碱法处理络合平衡体系

络合反应被广泛应用于络合滴定、氧化还原、沉淀滴定中，起到掩蔽、显色、指示剂的作用。体系中组分分布问题尤为重要。虽然在分析化学教材中，阐述了计算络合物溶液中平衡组分分布系数的方法，但由于络合体系较为复杂，学生在处理一些实际问题时，普遍感到一筹莫展。笔者将处理多元弱酸体系的思路应用于该体系之中，达到了简单快捷解决问题的目的。让我们通过一道习题的两种解法来说明。

例题:乙酰丙酮(L)与Al3+的络合物的lg K1～lg K3分别是8.6，6.9，5.8，则［AlL2］=［AlL3］时的pL约为:

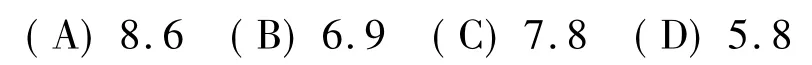
解法一:由于没有现成的结论和判断公式，多数学生利用分布分数的定义来解题:即

式中β为累积稳定常数。

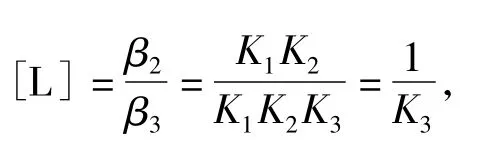
所以pL=lg K3=5.8，答案D正确。

可见，该法的解题步骤多，过程较长，达不到一目了然的目的。

由此，对照多元弱酸体系，我们可认为，溶液中络合物ALn平衡中，体系的组成受配位体L浓度的影响:

(1)体系的组成与pL关系以lg K1，lg K2，…，lg Ki，…，lg Kn－1，lg Kn为界，分为n+1种情况:

pL＜lg Kn，体系以ALn为主;

lg Kn＜pL＜lg Kn－1，体系以Hn－1A为主;

┇

pL＞lg K1，体系以A为主。

(2)若pL=lg Ki，则体系中以lg Ki为界的相邻两组分的分布分数相同。

需要说明的是:

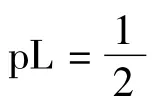
(2)在处理络合平衡时，特别要注意逐级形成常数与累积形成常数之间的换算，以免出现错误。

2 广义络合效应法解决副反应系数问题

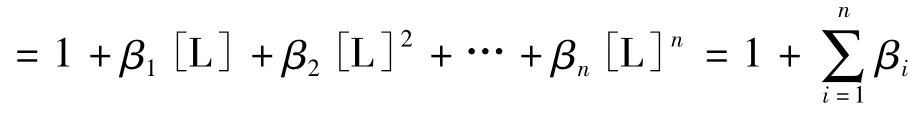
关于各副反应的相关信息见表1。

表1 副反应类型、受影响的物质以及相应的络合剂

这里需要说明的是，计算Y的酸效应系数时，要注意将已知的各级电离常数(Kai)换算为质子化常数:即lg K=p Kan，…，lg K=p Ka1，进而计算各级累积稳定常数(累积质子化常数)。

3 查漏补缺解决综合性习题问题

提高学生解决综合性习题能力是分析化学教学的目的之一。为此，必须对学生进行综合性解析训练。笔者在教学中发现，对于解综合性习题能力相对弱的学生，主要原因是其看不透题中涉及的知识点，搞不清计算步骤的先后顺序，导致解题出现困难。因此，笔者对学生进行了“查漏补缺”分析解题训练，达到了较好的效果。

查漏补缺是在分析题意和所给已知条件的基础上，先写出题中的最终目的求解公式，找出其中未知的因素，再写出计算该未知因素的计算公式，依次类推，直至所有的因素都可计算为止。这样就起到了提高基本概念综合应用能力的作用，对学生的解题表达能力也是一个很好的锻炼。我们看对以下例题的分析。

例题:以0.020mol·L－1EDTA滴定同浓度的Zn2+，可采用下述两种方法。一是在pH= 10.0的氨性缓冲溶液中(其中游离氨的浓度为0.20mol·L－1)，以铬黑T(EBT)为指示剂;二是在pH=5.5的六次甲基四胺缓冲溶液中，以二甲酚橙(XO)为指示剂。试通过计算终点误差进行比较和证明两种方法的可行性［1］。

已知:EDTA的lg K1～lg K6分别为－0.90，－1.60，－2.00，－2.60，－6.16，－10.26;lg KZnY=16.50;Zn－OH络合物的lgβ1～lgβ4分别为4.40，10.10，14.20，15.50;Zn－NH3络合物的lgβ1～lgβ4分别为2.37，4.81，7.31，9.46;pH=10.0时，pZnep(EBT)=12.2;pH=5.5时，pZnep(XO) =7.5。

查漏补缺过程如下:

(3)补缺:详见表2。