固体衬底上超薄膜表面的低能电子背散射系数计算研究

卓 俊 牛胜利 朱金辉 黄流兴

(西北核技术研究所 西安 710024)

薄膜材料在材料科学、微电子学器件和生物科学中均有广泛应用。现代材料科学发展及半导体技术中日益微型化的过程使制备的薄膜厚度低达数十nm，乃至更小，称为超薄膜。超薄膜的厚度测定日益引起人们重视，建立高分辨率的薄膜厚度测定方法是此领域的重要研究方向[1–4]。电子背散射方法是一种重要的测量方法[5,6]，基于薄膜背散射系数r与薄膜厚度D之间的对应关系确定薄膜厚度是此方法的一种重要手段。当入射电子能量为数十keV时，背散射电子在介质中的穿透深度较大，一般适用于测量几百nm厚的薄膜，此时r-D的关系较复杂；当入射电子能量仅数keV时，r与D存在简单的线性关系，且背散射电子穿透深度较小，适合于超薄膜的厚度测量。应用此方法需分析r-D线性段的变化规律，及其对薄膜测量厚度分辨率的影响。因此，研究固体衬底上超薄膜表面的低能电子背散射系数，对优化设计电子背散射法测量超薄膜厚度有重要意义。谭震宇等[7]使用 Monte Carlo 法计算了衬底上薄膜材料的低能电子背散射。然而，低能电子在介质中输运Monte Carlo模拟方法的选择，r-D线性区背散射常数C的变化规律等问题，仍需作进一步研究。

电子在介质中输运的Monte Carlo模拟方法常用的有两种[8]：(1) 多次散射模型下的压缩历史方法，在每一步输运中包含多次碰撞，其特点是计算速度快，但当电子能量降至数keV或更低时，多次散射公式不适用；(2) 模拟电子每一次碰撞过程的直接模拟方法，该方法适用于低能或介质为薄层、电子碰撞次数不很多的输运模拟[9]。针对低能电子在超薄膜/固体衬底结构材料表面的背散射问题，直接模拟方法更为适用。本文采用直接 Monte Carlo模拟方法，计算了能量为keV量级的电子在固体衬底上不同薄膜的电子背散射系数，分析了电子背散射系数r随薄膜厚度D的变化及r-D线性区背散射常数C与入射电子能量的关系。

1 电子直接Monte Carlo模拟方法

电子的直接Monte Carlo模拟是直接从物理问题出发，按粒子在介质中发生碰撞的先后顺序，逐个计算粒子发生的每一次碰撞过程的方法。模拟中电子输运步长s从宏观反应总截面Σt中随机抽样得到：

输运每一步中的碰撞散射角和损失能量从对应碰撞类型的微分截面中抽样得到。入射能量较低时，电子与物质的相互作用主要为非弹性散射和弹性散射过程。

低能电子在固体中的弹性散射采用量子力学分波法求解Dirac方程获得的Mott截面描述[10]：

式中，Ω为碰撞后电子的出射立体角，ƒ(θ)和g(θ)分别为求解相对论Dirac方程获得的入射与散射波函数。

对于低能电子与介质的非弹性碰撞过程，采用广义振子强度(GOS)模型下计算得到的电子非弹性散射截面：

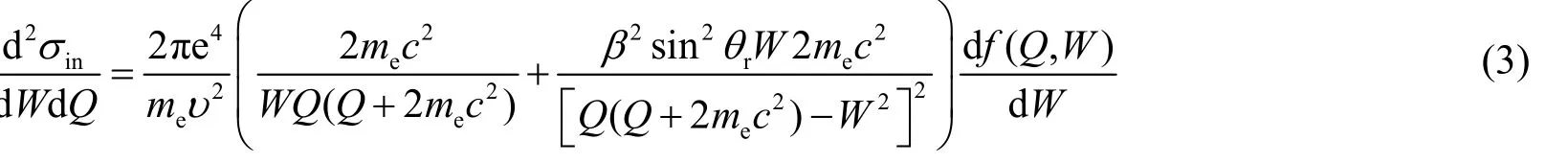
式中，W是碰撞中电子损失能量，Q为反冲能，它与电子散射极角θ一一对应，me为电子静止质量，υ为入射电子速度，β=υ/c(c为真空中光速)，θr为电子碰撞前运动方向与碰撞过程中电子动量改变方向的夹角，因子dƒ(Q,W)/dW为Born近似下的原子GOS，其大小决定了非弹性碰撞过程中的能量损失。在量子力学体系下解出的GOS表达式非常复杂，故求解非弹性碰撞截面时一般将靶物质看成是一种电介质，在该假设下应用介电模型得到的非弹性碰撞截面与使用量子力学方法给出的截面一致，但计算过程简单许多[11]。

按照上述原理，本文在PENELOPE程序包的基础上改造形成了电子输运的直接Monte Carlo模拟程序，并对电子在薄膜/衬底材料上的背散射过程进行了跟踪模拟。

2 测量薄膜厚度的电子背散射法原理

使用电子背散射系数确定薄膜厚度，首先要确定一定能量电子入射条件下，薄膜厚度与背散射电子系数间的变化关系。当电子入射固体表面时，有部分电子会从固体表面反射回来，称为背散射电子，定义背散射系数r为背散射电子数与入射电子数的比值。图1为电子垂直入射无定形C及金属Al、Cu、Ag、Au时的背散射系数r随入射电子能量E0的变化情况。

图1 电子在固体表面的背散射系数Fig.1 Monte Carlo simulation of the backscattering coefficient r as a function of the primary energy E0 for electrons impinging on bulk targets.

由图1可知，入射电子能量>1 keV时，原子序数较低的材料，电子在其表面发生背散射概率比高原子序数材料小得多，随着入射电子能量的上升，高原子序数厚样品物质的背散射系数可达0.5以上；当入射电子能量<1 keV时，高原子序数材料的背散射系数迅速减小，随着能量的降低，低原子序数材料的背散射系数逐渐超过高原子序数材料。当薄膜材料的原子序数Zf与衬底材料的原子序数Zs存在较大差异时，薄膜/衬底材料表面的电子背散射系数大小将随薄膜厚度的增加而逐渐从衬底材料的背散射系数rs变化为薄膜材料的背散射系数rf。研究表明：当入射电子能量为十余keV或数十keV时，薄膜/衬底的r-D曲线存在2–3个线性段[1]，r与D间的关系较复杂；当入射电子能量降至几 keV时，r-D曲线的前端仅存在单一线性增长关系[7](图2)，以此可测定衬底上薄膜的厚度。

式中，C称为背散射常数，通过实验测量或模拟计算统计分析得到，当薄膜材料和衬底材料确定后，|C|的大小决定了测量的厚度分辨率，r0为衬底的背散射系数，图中LM表示r-D曲线的线性段长度。

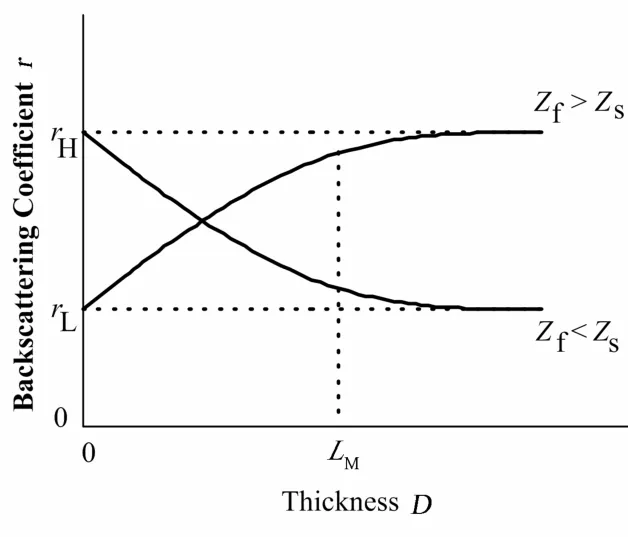
图2 电子背散射法测量薄膜厚度原理图Fig.2 Principle of the electron backscattering method for thickness determination of ultra-thin films.

3 计算结果及讨论

基于上述原理及方法，模拟了电子垂直入射薄膜/衬底材料的背散射过程，计算中电子的截断能量为50 eV，并取衬底材料厚度远大于入射电子射程。

3.1 薄膜/衬底的r-D曲线

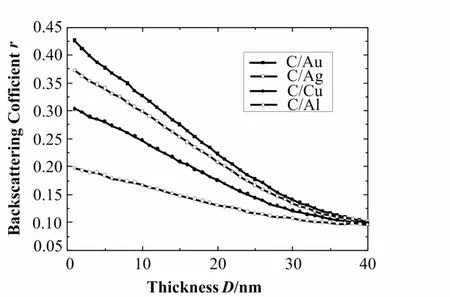
薄膜/衬底的原子序数(Zf,Zs)可分为Zf>Zs和Zf

在Au /Al这种Zf>Zs情形下，薄膜/衬底材料的电子背散射系数r小于相同入射能量下原子序数为Zf固体(以下简记为Zf固体)的电子背散射系数。假设入射电子能量为E0，Zf固体和Zs固体的电子背散射系数分别为rf和rs，则薄膜/衬底的背散射系数r随薄膜厚度D的变化相应在rsZs的相反，r在rf

图3 不同入射电子能量下Au /Al和Al /Au的r-D曲线Fig.3 Backscattering coefficient r versus film thickness D for Au films on Al substrate and Al films on Au.Substrate,■1keV,□2keV,●3keV,○4keV,▲5keV

为反映衬底改变对r-D曲线的影响，计算了E0=2 keV时，C/Au、C/Ag、C/Cu和C/Al的r-D曲线(如图4)。薄膜材料一定时，Zs与Zf的差异越大，r-D曲线线性段斜率的绝对值越大，即测量薄膜厚度分辨率越高。此外，四种不同衬底情况下的r-D曲线线性区范围均～26 nm，表明在薄膜材料相同情况下，只要Zf与Zs的差异较大，衬底改变对Zs曲线线性区范围LM的影响不大。

图4 E0=2 keV，C/Au，C/Ag，C/Cu，C/Al的r-D曲线Fig.4 Backscattering coefficient r versus film thickness for C films on different bulk substrates.

3.2 背散射常数C随能量变化

入射电子能量E0较高时，电子背散射方法测定薄膜的分辨率较低，因为入射电子能量越高，背散射电子在固体中深度分布范围越大，在薄膜中单位厚度上背散射电子出射数就越少，因此，通常采用降低入射电子能量来提高薄膜厚度测量的分辨率。

图5为Au衬底上不同薄膜背散射常数C的绝对值随入射电子能量E0的变化情况，其中背散射常数C系由对r-D曲线线性段数据进行最小二乘法拟合处理得到。可以看出，随着能量的降低，背散射常数C的绝对值逐渐增大，当能量下降到一定程度后，由于作为衬底的Au材料的背散射系数快速下降，导致薄膜与衬底间的背散射系数差异减小，降低了薄膜测量的厚度分辨率。不同薄膜材料在不同衬底上达到最大分辨率时的能量不同，如在Au衬底上，C、Al、Cu和Ag薄膜的最大分辨能量约分别为0.8、1.4、1.7、2.2 keV。另外，当入射能量降至数百eV时，Ag/Au、Cu/Au的C曲线会出现较大的C值，但由于此时高原子序数薄膜/衬底材料的r-D曲线线性段范围LM太小(<1 nm)，因此不存在实际的应用价值。

图5 背散射常数C随入射电子能量E0的变化曲线Fig.5 Absolute value of backscattering constant C of thin films versus primary energy E0.

4 结论

使用一种适合模拟低能电子在固体材料中输运的Monte Carlo方法——直接Monte Carlo方法，计算了低能电子在衬底上超薄膜表面的背散射。结果表明：keV级低能电子入射条件下，薄膜/衬底的r-D曲线初始范围仅存在单一的线性区，且在背散射常数C随入射能量的变化曲线中存在一极大值，当入射电子能量大于极大值能量时，薄膜分辨率随入射电子能量E0的减小而提高；当入射电子能量小于极大值能量时，薄膜分辨率随入射电子能量E0迅速降低。这个规律可以作为超薄膜测量中入射电子能量选择的重要参考依据。

1 Niedrig H. Opt Acta, 1977, 24(6): 679–691

2 Niedrig H. J Appl Phys, 1982, 53(4): 15–49

3 巩 岩, 陈 波, 尼启良, 等. 高能物理与核物理, 2005,29(11): 253–258 GONG Yan, CHEN Bo, NI Qiliang,et al. High Energy Phys Nucl Phys, 2005, 29(11): 253–258

4 王科范, 徐彭寿, 张伟风, 等. 核技术, 2008, 31(4):255–259 WANG Kefan, XU Pengshou, ZHANG Weifeng,et al.Nucl Tech, 2008, 31(4): 255–259

5 Schlichting F, Berger D, Niedrig H. Scanning, 1999, 21(3):197–203

6 Maurizio D. American Nuclear Society Topical Meeting in Monte Carlo, Chattanooga, Tennessee, 2005

7 谭振宇, 夏曰源. 物理学报, 2002, 51(7): 1506–1511 TAN Zhenyu, XIA Yueyuan. Acta Phys Sin, 2002, 51(7):1506–1511

8 Fernández-Varea J M, Mayol R, Barό,et al. Nucl Instr Meth Phys Research, 1993, B73: 447–473

9 卓 俊, 牛胜利, 黄流兴, 等. 计算物理, 2009, 26(4):586–590 ZHUO Jun, NIU Shengli, HUANG Liuxing,et al. Comp Phys, 2009, 26(4): 586–590

10 Jablonski A, Salvat F, Powell C J. J Phys Chem Ref Data,2004, 33(2): 409–451

11 Fernández-Varea J M, Mayol R, Liljequist D,et al. J Phys:Condens Matter, 1993, 5: 3593–3610