三维高精度霍尔探头的位置和角度标定

张 伟 周巧根 王宏飞 陆 杰

(中国科学院上海应用物理研究所 上海 201800)

插入件是第三代同步辐射光源的重要标志，上海光源(SSRF)首期束线的插入件包括两台扭摆器、两台真空内波荡器和一台可变椭圆极化波荡器(EPU100)[1,2]。EPU100长 4.3 m，采用 APPLE-II型[3]磁铁结构，能形成各种分布的周期性三维磁场，使高能电子束通过时产生各种极化模式的同步辐射光。

波荡器磁场质量直接影响同步辐射光的性能，因此，精确测量波荡器磁场以进一步优化磁场性能，尤为重要。三维霍尔点测量系统(美国 ADC公司)可同时测量磁场三个方向的分量，还可沿x、y、z轴作自动扫描测量。三个平面霍尔探头沿z方向依次两两垂直地粘在一个测量臂上，构成一个三维测量探头。每个平面霍尔探头事先已作精确的霍尔电压标定，包括磁场非线性标定和温度系数标定。但是，三个探头独立地位于测量臂上的三个点上，相互间存在位置差异及正交性误差，各探头测得的并非同一空间点的磁场，且磁场的三个分量也会影响到各探头的测量结果。因此，须对三个探头间的位置及正交性进行标定，并修正磁场测量结果。我们用EPU100产生的各种周期性磁场对三个探头的正交性作了精确标定。

1 位置标定

三个霍尔探头(探头x、y和z)分别用于测量磁场分量Bx、By和Bz。设三个探头在测量臂上依次沿z轴排列，探头u和v (u,v=x,y,z)的灵敏中心在z向的间隔为zDisuv。同时，由于安装误差，三个探头的灵敏中心在x和y方向也会存在小的间隔，分别用xDisuv和yDisuv表示。为精确测量xDisuv、yDisuv和zDisuv，我们采用一个顶角为90°的纯铁楔形块，一长方体永磁块吸附在楔形块底部，永磁块的磁化方向与楔形块底面垂直(图1)。

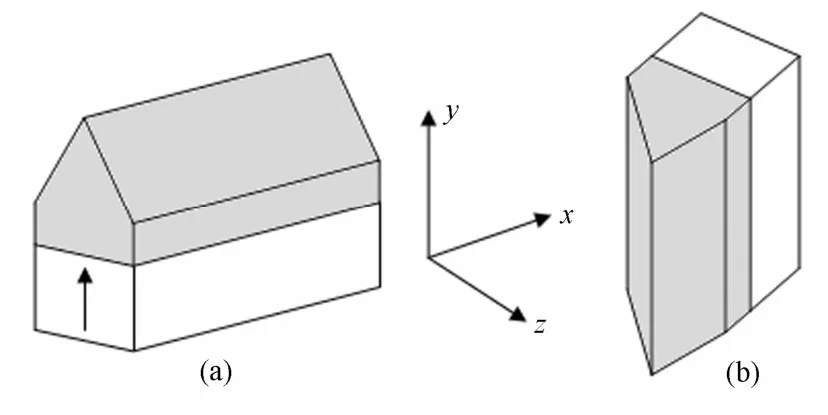
图1 楔形块水平放置(a)和垂直放置(b)示意图Fig.1 Schematics of an iron wedge placed on a permanent magnet block, with the top edge along (a) the x-axis and the y-axis (b).

当楔形块水平放置时，其上方的磁场沿楔形块横向z的分布如图2(a)所示。由于该楔形块的特殊结构，其By(平行于永磁块磁化方向)沿z轴为对称分布，而Bz沿z轴为反对称分布，Bz的零点对应于By的峰值点。当测量臂沿z轴扫描时，由其上的霍尔探头z和霍尔探头y测得的Bz的零点位置和By的峰值点位置必将存在位置偏移，偏移量为zDisyz。

改变楔形块的放置方式如图1(b)所示，使三维探头沿z向扫描测量时，其Bx沿z向为对称分布，而Bz沿z向仍为反对称分布，如图2(b)。此时，Bz的零点位置和Bx的峰值点位置的偏移即为zDisxz。霍尔探头x和y在z轴方向上的位移为xDisyz，zDisxy=zDisxz－zDisyz。

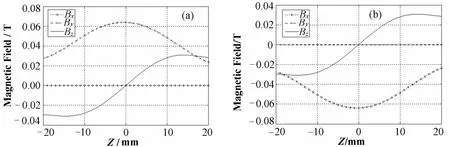
图2 楔形块三维磁场沿纵向的分布 (a) 水平放置，(b) 垂直放置Fig.2 The field components on a line along the z-axis with the wedge oriented along (a) y-axis and (b) x-axis.

改变三维霍尔探头扫描测量方向及楔形块的放置方式，可得三个霍尔探头在x轴和y轴方向上的位移(xDisyz、xDisxz、xDisxy和yDisyz、yDisxz、yDisxy)。用三维霍尔探头测量波荡器磁场时，三个探头给出的是不同空间点上的三个磁场分量。为得到同一点上的三个磁场分量，需在一定范围内进行矩形网格的场图测量，再根据三个探头在空间的位置关系，利用数值插值的方法得到所需的场图分布。一般情况下，三个探头在x和y方向的位置偏差都很小。对于实际的波荡器，这种很小的横向位置偏差只影响磁场的纵向分量Bz的测量结果，利用磁场的无旋性就可对此作线性校正。

用三维霍尔探头测得的位置偏移量(单位：mm)分别为：zDisxy=7.88，zDisyz=9. 76，zDisxz=17.64；xDisxy= 0.37，xDisyz= –0.06，xDisxz=0.31；yDisxy= –0.21，yDisyz=1.24，yDisxz=1.03。

2 角度标定

通过对三个探头的位置标定，得到三探头在空间同一点处的三个霍尔输出电压。但是，由于三个探头间不可避免的非严格正交，以及平面霍尔效应[4]等，这些霍尔输出是实际磁场的三个分量同时贡献的。设、和为三个探头在同一空间点处测得的三个磁场分量，则此处实际的三个磁场分量可表示为：

其由两部分组成：探头间不正交导致的两个方向上的磁场分量在第三个方向上投影的线性部分以及平面霍尔效应及张力霍尔效应带来的二次项部分，这里用Cmn和Cmnl表示它们间关系。对于较小的非正交关系，Cxx、Cyy和Czz可认为等于1。另外，平面霍尔效应及张力霍尔效应都较小，Cmnl认为0。

2.1 APPLE-II型可变椭圆极化波荡器磁场分布

图3为APPLE-II型可变椭圆极化波荡器的几种磁铁分布图，四个标准的纯永磁Halbach-Type磁排列A、B、C和D分布在电子轨道的上方和下方组成两对平行的永磁块排列。永磁块为钕铁硼材料，其磁导率接近 1，因而不同永磁块所产生的磁场可以线性叠加。每排磁排列可独立的沿长度方向作纵向移动，从而产生不同极化模式下的磁场分布。在中心轴线上的磁场Bx、By和Bz沿纵向z的分布可表示为[5]：

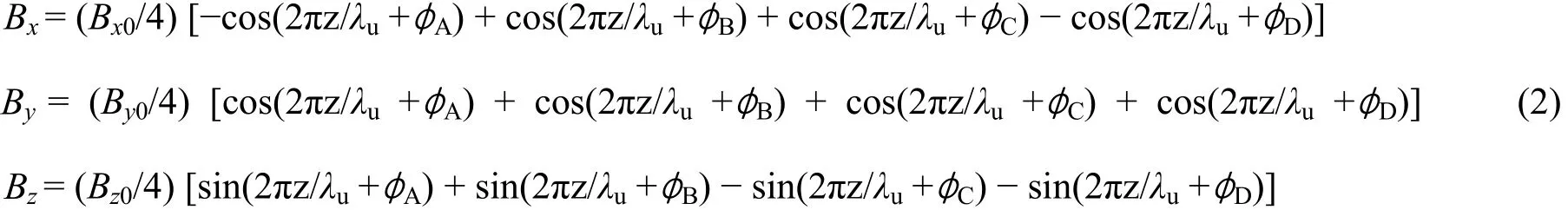
式中，λu为波荡器的周期长度，φA、φB、φC和φD分别表示磁排列A、B、C和D在纵向相对于固定参考点的相位(称为位置相位)。Bx0/4、By0/4和Bz0/4分别代表单排磁化块在中心轴上产生的磁场三个分量的峰值，由四排永磁块的几何关系及永磁块的磁化强度决定。

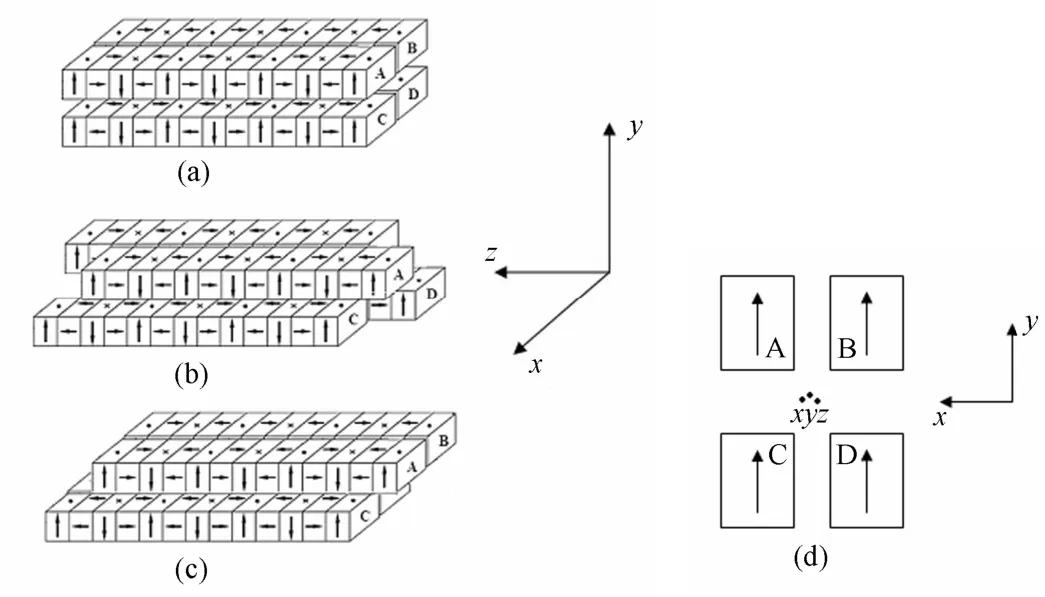
图3 不同磁排列示意图(a) 四排无相对位移, (b) 对角排A、D相对于B、C有半个周期λu/2的位移,(c) 上两排相对下两排有λu/2的位移, (d) 切面图Fig.3 Schematics of magnet block arrays with APPLE-II type.(a) No phase shift in four arrays, (b) Shift λu/2 between AD and BC,(c) Shift λu/2 between up arrays and down arrays, (d) Cross section.

图3(a)所对应的是φA=φB=φC=φD=0，这时Bx=Bz=0，By=By0cos(2πz/λu)，磁场只有垂直方向分量By；图 3(b)对应的是φA=φD=π，φB=φC=0，这时By=Bz=0，Bx=Bx0cos(2πz/λu)，磁场只有水平分量Bx；而图 3(c)对应于φA=φB=π，φC=φD=0，此时Bx=By=0，Bz= −Bz0sin(2πz/λu)，磁场只有纵向分量Bz。

2.2 C系数的确定

由于椭圆极化波荡器磁场的特殊性，理想情况下上述三种磁排列下的三维空间磁场分布都具有以下特点：磁场的某一分量满足周期性正弦或余弦分布，而磁场的其他分量为零。在这种分布下，我们可通过测量不同磁排列条件下波荡器中心轴线上的三维磁场分布来研究三维霍尔探头间由于不正交而产生的相互影响。

以图 3(a)四排磁排列无相对位移的水平极化模式为例，理想磁场只有垂直分量By，Bx、Bz为零。实际测量到的磁场分布如图 4(a)，其中三个探头在纵向的位置偏移已予以校正，而横向偏移没有校正。由图测到的Bx分量和Bz分量不为0，而是有类似正弦分布的小量，其中Bx分布与By基本同相位(或反相位)，而Bz与By不同相位。同相位部分正是由于探头的不严格正交形成的，而Bz与By间的不同相位则是由探头y和探头z在y方向存在的位置偏移产生的。忽略小量间的相互影响，实际磁场的水平分量和纵向分量可表示为：

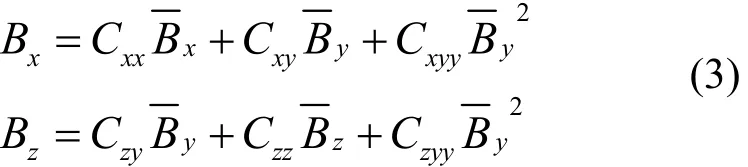
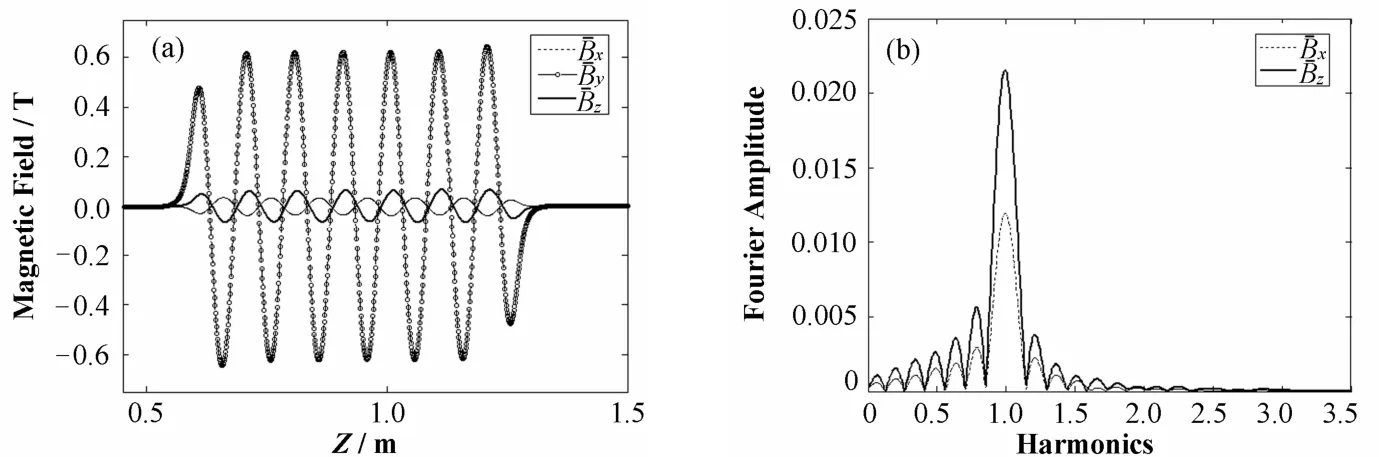
图4 水平极化模式下测到的磁场分布(a)及其频谱分析(b)Fig.4 The configuration (a) and Fourier spectrum (b) of magnetic field in horizontal polarization after position correction.

分别对和作频谱分析，结果如图4(b)，在基波n=1处，两个磁场分量均存在比较大的峰，而在n=2处却没有。可见B—x和B—z中只存在一次谐波，说明公式(3)中只存在线性项而没有二次项，即可确定Cxyy和Czyy为0。因此，公式(3)可简化为：

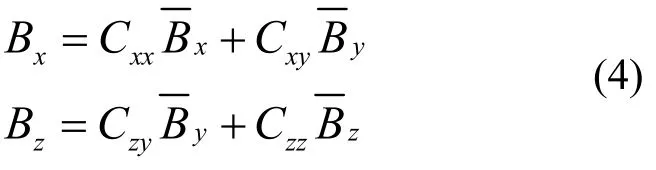
对Bx和Bz作频谱分析，并改变Cxy和Czy的值，使得到的一次谐波为最小，Cxy和Czy的值便由此确定。此时得到的三个磁场分量如图 5(a)所示，图中还存在与By的相位相差90°的Bz分布。根据磁场的无旋性，对Bz作修正：

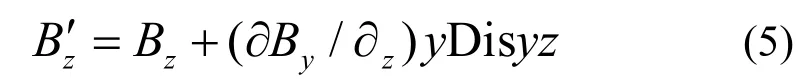
得到的Bz几乎为0，如图5(b)所示。改变磁排列方式如图3(b)和图3(c)，用上述方法同样可得Czx、Cyx、Cyz、Cxz以及Cyxx、Czxx、Cyzz、Cxzz。

图5 角度校正后测得的水平极化模式下中心轴线上的磁场分布 (a) 修正前，(b) 修正后Fig.5 The field configuration after non-orthogonality correction.(a) Without curl correction, (b) Correction with curl value 0.

为确定Cxyz、Cyxz和Czxy三个系数，我们也可以构造这样一种磁场：其中的一个分量为零，而另外两个分量不为零。例如调整四排磁排列的位置相位，使其产生圆极化模式的磁场，此时在中心轴上磁场的水平分量和垂直分量的峰值相等，相位差为90°，而磁场的纵向分量Bz为0。这时，式(1)中Bz简化为：

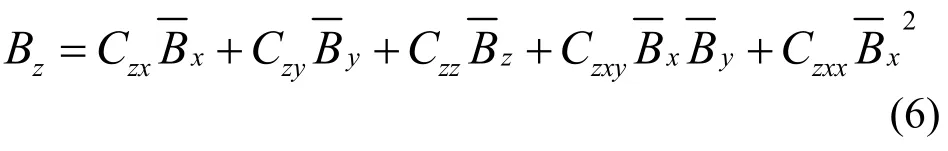
对其作频谱分析，并使二次谐波达到最小，便可得到Czxy。同样通过构造其它磁场分布，可确定Cyxz和Cxyz。

对于我们使用的三维霍尔探头，二次项系数均近似为0，测得的线性系数为：

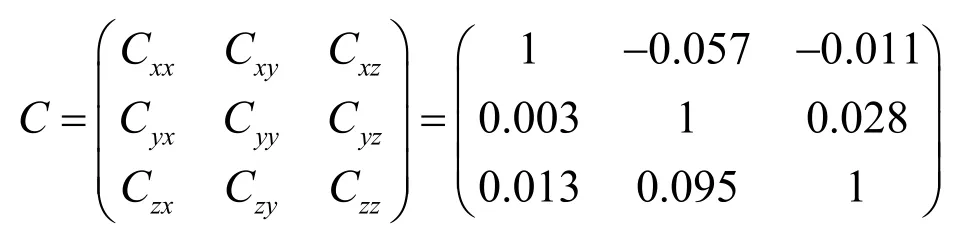
3 结论

由三个平面霍尔探头构成的三维测量探头已成功应用于上海光源一台长4.3 m APPLE-II结构的可变椭圆极化波荡器和两台小气隙真空内波荡器的磁场测量中。利用特殊设计的锲形块磁铁产生的磁场可准确测量三个探头灵敏中心的空间相对位置，从而解决了三个探头不能测量同一空间点磁场的问题。利用 APPLE-II结构的可变椭圆极化波荡器可方便产生各种磁场分布的特点，并对测量得到的各磁场分量作频谱分析，可得到三个探头间的角度关系。利用这种方法还能测量探头的平面霍尔效应和张力霍尔效应等。实验证明这种方法是有效的，能满足各种螺旋形磁场精确测量的要求。

1 ZHOU Qiaogen, ZHANG Wei, ZHANG Miao,et al.IEEE Trans Appl Supercond, 2010, 20(3): 254–257

2 ZHANG Wei, LU Jie, ZHOU Qiaogen,et al. IEEE Trans Appl Supercond. 2010, 20(3): 296–299

3 Sasaki S, Kakuno K, Takada T,et al. Nucl Instr Meth,1993, A331, 763–767

4 McGuire T R, Plotter R I. IEEE Trans Magn, 1975,MAG-11: 1018–1037

5 Hwang C S, Shuting Yeh. Nucl Instr Meth, 1999, A420:29–38