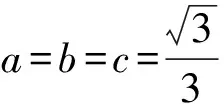2010年数学高考模拟卷(五)
2010-06-08王希年
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的4个选项中,只有1项是符合题目要求的.
( )
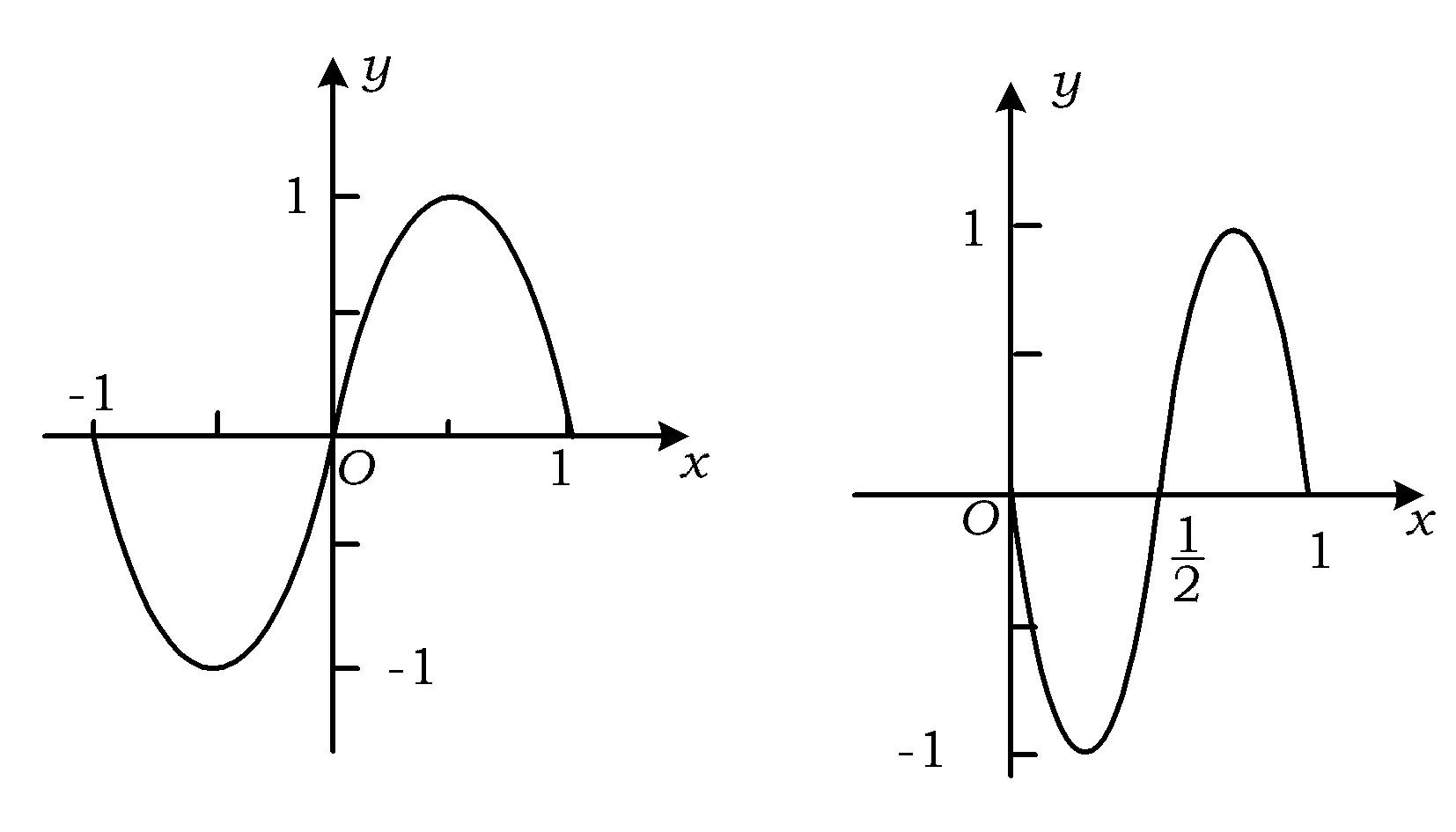
图1 图2
2.下列命题中,m,n表示2条不同的直线,α,β,γ表示3个不同的平面.①若m⊥α,n∥α,则m⊥n;②若a⊥γ,β⊥γ,则α∥β;③若m∥α,n∥α,则m∥n;④若α∥β,β∥γ,m⊥α,则m⊥γ.正确的命题是
( )
A.①③ B.②③ C.①④ D.②④
3.已知函数f(x)=sinπx的图像如图1所示,则图2所示的函数图像对应的函数解析式可以是
( )
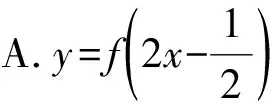
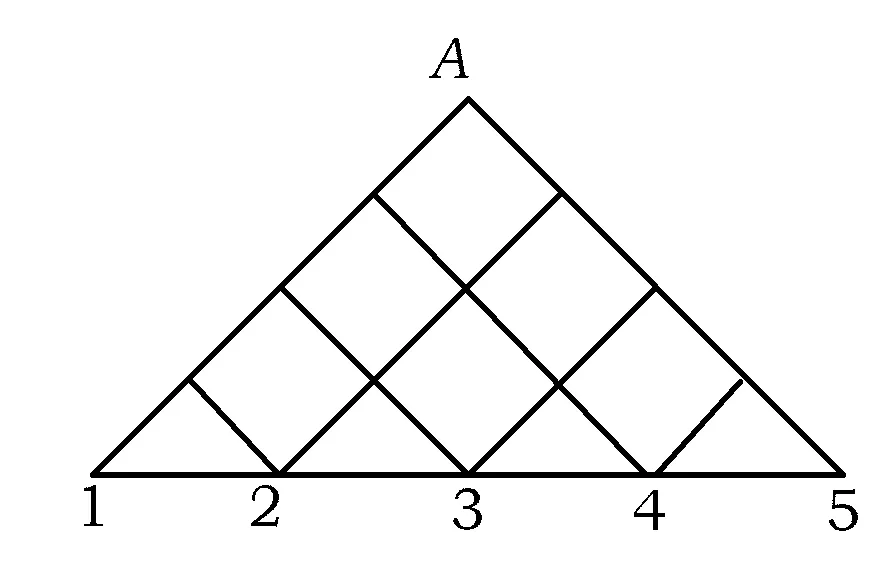
图3
4.小球A在如图3所示的通道由上到下随机地滑动,最后在下底面的某个出口落出,则一次投放小球,从“出口3”落出的概率为
( )
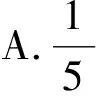
( )


图4
6.下列命题中是假命题的是
( )
A.存在m∈R,使得f(x)=(m-1)·xm2-4m+3是幂函数,且在(0,+∞)上递减
B.任意a>0,函数f(x)=ln2x+lnx-a有零点
C.存在α,β∈R,使得cos(α+β)=cosα+sinβ
D.任意φ∈R,函数f(x)=sin(2x+φ)都不是偶函数
7.长为10 cm的线段AB的2个端点A,B分别在x轴的正半轴和y轴的正半轴上滑动,设坐标轴的单位长度是1 cm.若端点B从点(0,8)处以1 cm/s的速度向下滑动,则端点A在t=2 s时滑动的瞬时速度是
( )
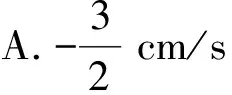
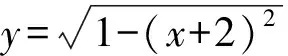
( )
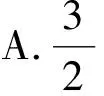
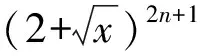
( )
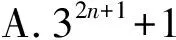
10.曲线x2+y2-ay=0与ax2+bxy+x=0有且只有3个不同的公共点,那么
( )
A.(a4+4ab+4)(ab+1)=0 B.(a4-4ab-4)(ab+1)=0
C.(a4+4ab+4)(ab-1)=0 D.(a4-4ab-4)(ab-1)=0
二、填空题:本大题共7小题,每小题4分,共28分.
11.设集合M={m|m=5n+2n,n∈N*,且m<100},则集合M中所有元素的和为________.
12.棱长为1的正方体和它的外接球与一个平面相交得到的截面是一个圆及它的内接正三角形,那么球心到截面的距离等于________.
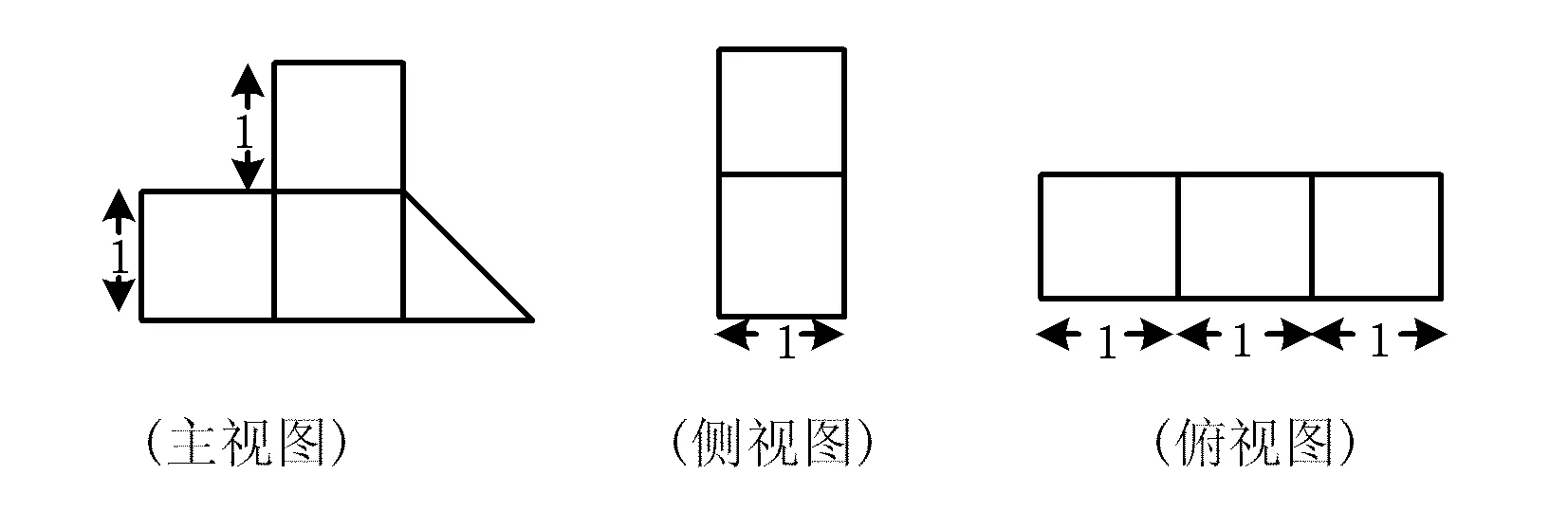
图5
13.设等比数列{an}的公比为q,前n项和为Sn.若Sn+1,Sn,Sn+2成等差数列,则q=________.
14.一个几何体按比例绘制的三视图如图5所示(单位:m),则该几何体的体积为________m3.

图6
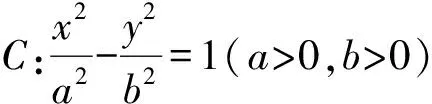
16.已知{an}为等差数列,且an≠0,公差d≠0.现有下列3个等式:
根据上面的几个等式,试归纳出更一般的结论:________.
三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.

图7
18.在△ABC中,内角A,B,C所对应的边长分别是a,b,c.
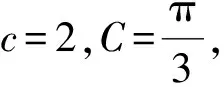
(2)若sinC+sin(B-A)=sin2A,试判断△ABC的形状.
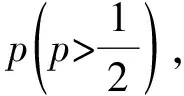
(1)在图7中,第一、第二判断框应分别填写什么条件?
(2)求p的值;
(3)设ζ表示比赛停止时已比赛的局数,求随机变量ζ的分布列和数学期望Eζ.

图8
20.如图8,在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB=90°,AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
(1)证明:CD⊥平面BEF;
(2)设PA=k·AB,且二面角E-BD-C为60°,求k的值.
21.已知抛物线的顶点在原点,焦点在y轴的负半轴上,过其上一点P(x0,y0)(x0≠0)的切线方程为y-y0=2ax0(x-x0)(a为常数).
(1)求抛物线方程.
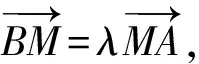
(3)在第(2)小题的条件下,当λ=1,k1<0时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标的取值范围.
22.(本小题满分15分)已知函数f(x)=ln(ax+1)+x3-x2-ax.
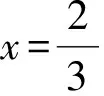
(2)若y=f(x)在[1,+∞)上为增函数,求实数a的取值范围;
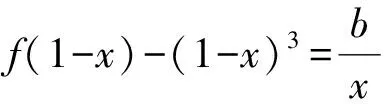
IB选修参考题
1.坐标系与参数方程模块:
(1)将极坐标方程化为普通方程,并选择恰当的参数写出它的参数方程;
(2)若点P(x,y)在该圆上,求x+y的最大值和最小值.
2.不等式选讲模块:
已知a,b,c为正实数,且ab+bc+ca=1.
(1)求a+b+c-abc的最小值;
参考答案
1.C 2.C 3.B 4.D 5.B 6.D 7.D
8.B 9.D 10.B
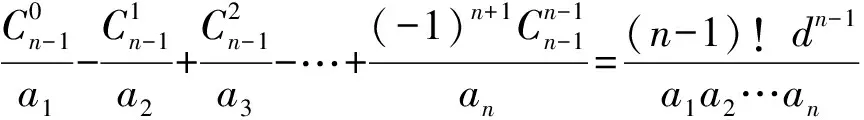
17.1∶(-6)∶5∶(-8)
18.解(1)由余弦定理及已知条件得
a2+b2-ab=4.

得ab=4.联立方程组
解得
a=2,b=2.
(2)由题意得
sin(B+A)+sin(B-A)=sin2A,
展开整理得
sinBcosA=sinAcosA.
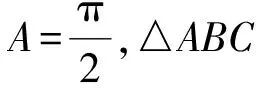
综上所述,△ABC为等腰或直角三角形.
19.解(1)程序框图中的第1个条件框应填M=2,第2个应填n=6.
注意:答案不唯一.
譬如:第1个条件框填M>1,第2个条件框填n>5,或者第一、第二条件互换.
(2)依题意,当甲连胜2局或乙连胜2局时,第2局结束时比赛结束,有
解得
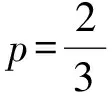

(3)依题意知,ζ的所有可能值为2,4,6.
若该轮结束时比赛还将继续,则甲、乙在该轮中必是各得1分,此时,该轮比赛结果对下轮比赛是否停止没有影响.从而有
因此随机变量ζ的分布列如表1所示.
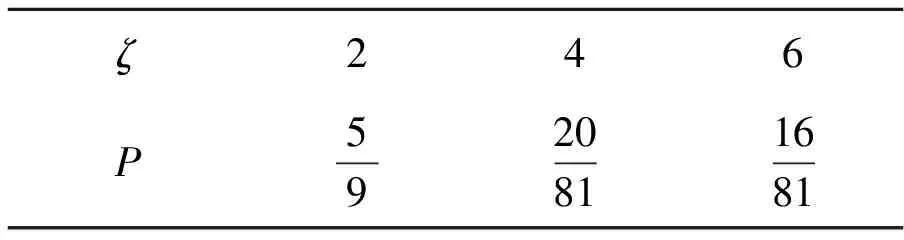
表1 ζ的分布列
故
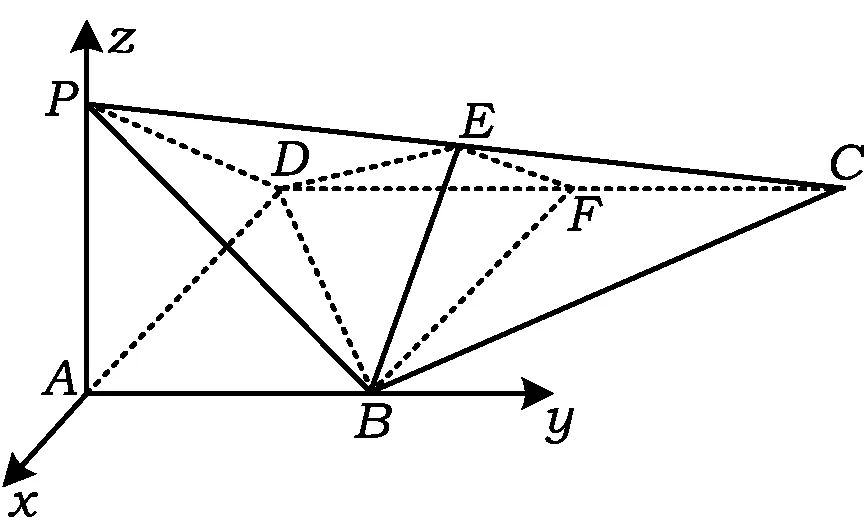
图9
20.(1)证明以点A为原点,建立如图9所示的空间直角坐标系A-xyz,则B(0,1,0),C(-2,2,0),D(-2,0,0).设PA=k,则
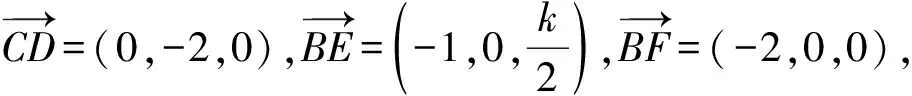
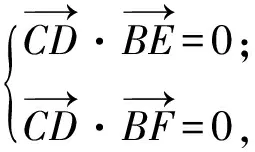
则
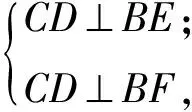
于是CD⊥平面BEF.
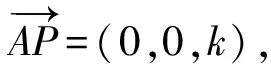
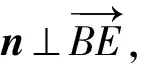
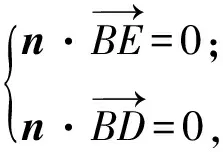
得
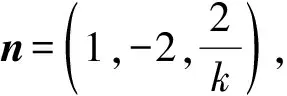
得
解得
21.解(1)由题意可设抛物线的方程为
x2=-2py(p>0).
由过点P(x0,y0)(x0≠0)的切线方程为
y-y0=2ax0(x-x0),
得
因此
故抛物线的方程为y=ax2(a<0).
(2)直线PA的方程为
y-y0=k1(x-x0),
联立方程
得
ax2-k1x+k1x0-y0=0,
于是
同理可得
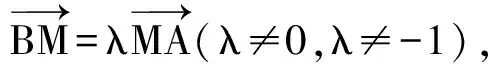
xM-xB=λ(xA-xM),
即
故线段PM的中点在y轴上.
(3)由λ=1,P(1,-1),可知a=-1,因此
A(-k1-1,-(k1+1)2),B(k1-1,-(k1-1)2),
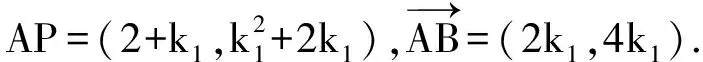
因为∠PAB为钝角,且P,A,B不共线,所以

即
得
又k1<0,所以
解得



22.解(1)由题意得
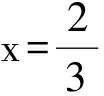

(2)因为f(x)在[1,+∞)上为增函数,所以
在[1,+∞)上恒成立.
若a=0,则f′(x)=x(3x-2),因此f(x)在[1,+∞)上为增函数成立;
若a≠0,由ax+1>0对x>1恒成立,知a>0,则3ax2+(3-2a)x-(a2+2)≥0对x∈[1,+∞)上恒成立.令
g(x)=3ax2+(3-2a)x-(a2+2),

从而g(x)在[1,+∞)上为增函数.故只要g(1)≥0即可,即
-a2+a+1≥0,
解得
又因为a>0,所以
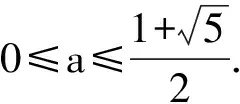
(3)若a=-1时,由方程
可得
即b=xlnx-x(1-x)2+x(1-x)=xlnx+x2-x3
在x>0上有解,即问题可转化为求函数g(x)=xlnx+x2-x3的值域.
令h(x)=lnx+x-x2,由
且x>0,可得当0
h(x)≤h(1)=0,
而h(x)可以无穷小,故b的取值范围为(-∞,0].
IB选修参考答案
1.解(1)普通方程为
x2+y2-4x-4y+6=0,
即
(x-2)2+(y-2)2=2,

2.(1)解因为(a+b+c)2≥3(ab+bc+ca)=3.又a,b,c>0,所以
又由a,b,c>0,可得

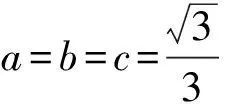
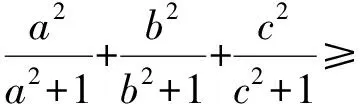
所以