2010年数学高考模拟卷(四)

参考公式：

棱柱的体积公式V=Sh，其中S表示棱柱的底面积,h表示棱柱的高；

球的表面积公式S=4πR2，其中R表示球的半径；

如果事件A,B互斥,那么P(A+B)=P(A)+P(B)；

如果事件A,B相互独立,那么P(A·B)=P(A)·P(B)；

如果事件A在一次试验中发生的概率是p,那么n次独立重复试验中事件A恰好发生k次的概率为

一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的4个选项中,只有1项是符合题目要求的.

1.集合A={y∈R|y=lgx,x>1},B={-2,-1,1,2},则下列结论正确的是

( )

A.A∩B={-2,-1} B.(CRA)∪B=(-∞,0)

C.A∪B=(0,+∞) D.(CRA)∩B={-2,-1}

( )

A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件

( )

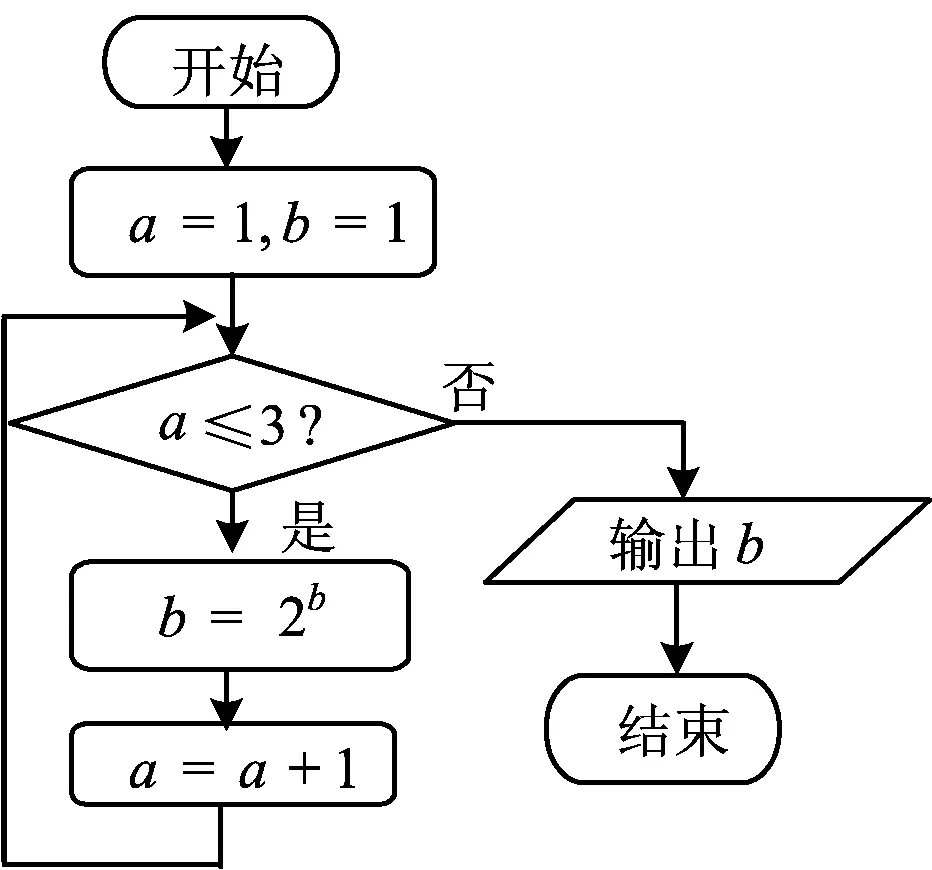
图1

( )

5.如图1所示的程序框图，输出的结果为

( )

A．1 B．2 C．4 D．16

图2

( )

7.一空间几何体的三视图如图2所示，则该几何体的表面积为

( )

( )

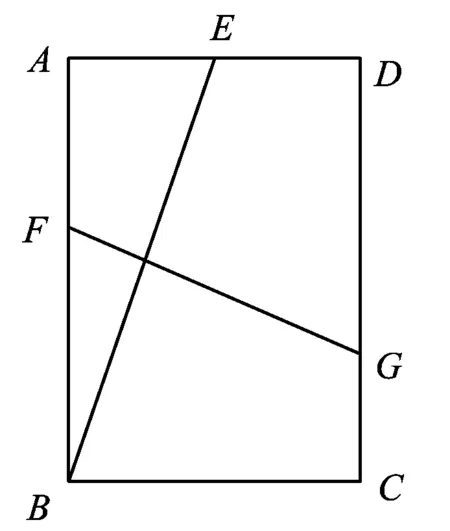
图3

9.如图3所示，在矩形ABCD中，AB=12，AD=10，将此矩形折叠使点B落在AD边的中点E处，则折痕FG的长为

( )

10.对于实数x，符号[x]表示不超过x的最大整数，例如[π]=3，[-1.08]=-2，定义函数f(x)=x-[x],则下列命题中正确的是

( )

A．f(x)=1 B．函数f(x)是周期函数

二、填空题：本大题共7小题，每小题4分，共28分．

图4

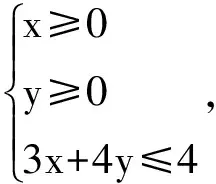
12.设等差数列{an}的前n项和为Sn，若S3=9,S6=36，则a7+a8+a9=________.

13.某赛季，甲、乙2名篮球运动员都参加了比赛，他们每场比赛得分的情况用如图4所示的茎叶图表示，则甲、乙2名运动员比赛得分的中位数之和是________

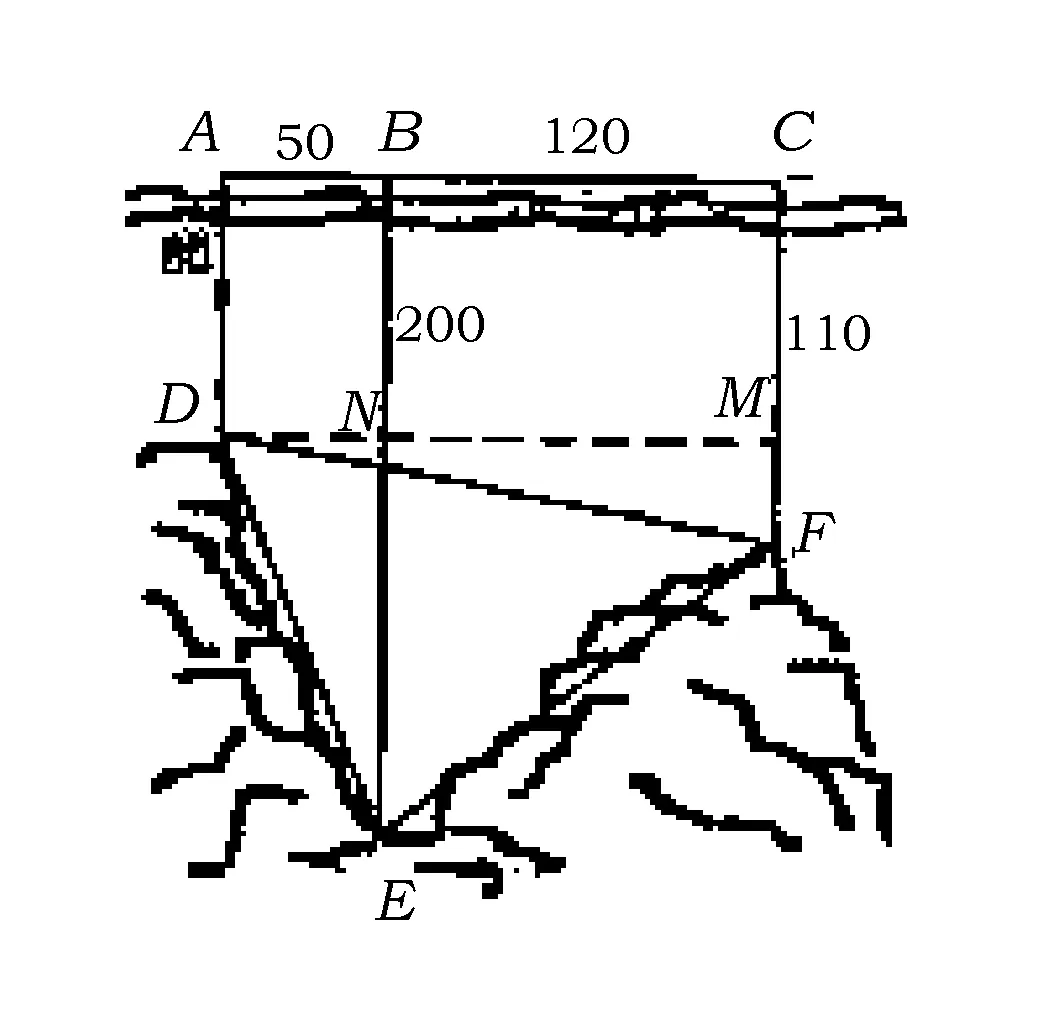
图5

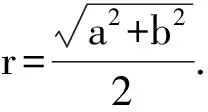
15.如图5，为了解某海域海底构造，在海平面内一条直线上的点A，B，C处进行测量，已知AB=50 m，BC=120 m，于点A处测得水深AD=80 m，于点B处测得水深BE=200 m，于点C处测得水深CF=110 m，则∠DEF的余弦值为________.

16.2009年浙江省新课程自选模块考试试卷中共有18道试题，要求考生从中选取6道试题进行解答，其中考生甲第2，6，9，13，14，17，18题一定不选，考生乙第7，9，13，14，17，18题一定不选，且考生甲与乙选取的6道题没有1道题是相同的，则满足条件的选法种数共有________(用数字作答).

图6

三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.

(1)求函数f(x)的表达式；

(2)在△ABC中,角A，B，C所对应的边分别为a,b,c，若f(C)=1，且AC+BC=10，求△ABC面积的最大值.

19．2008年中国北京奥运会吉祥物由5个“中国福娃”组成，分别叫贝贝、晶晶、欢欢、迎迎、妮妮.现有8个相同的盒子，每个盒子中放1个福娃，每种福娃的数量如表1所示.

表1 每种福娃的数量

从中随机地选取5个.

(1)求选取的5个恰好组成完整“奥运吉祥物”的概率.

(2)若完整地选取奥运会吉祥物记10分；若选出的5个中仅差1种记8分；差2种记6分；以此类推.设ζ表示所得的分数，求ζ的分布列及数学期望.

图7

20.如图7,已知等腰直角三角形RBC，其中∠RBC=90°，RB=BC=2．点A,D分别是RB,RC的中点，现将△RAD沿着边AD折起到△PAD的位置，使PA⊥AB，连结PB,PC．

(1)求证：BC⊥PB；

(2)求二面角A-CD-P的余弦值．

(1)求椭圆的方程.

(3)在第(2)小题的条件下，试问x轴上是否存在异于点C的定点Q，使得以MP为直径的圆恒过直线DP,QM的交点.若存在，求出点Q的坐标；若不存在，请说明理由.

22.已知函数f(x)=x2+lnx-ax,a∈R.

(1)若a=3，求函数f(x)的单调减区间;

(2)若函数f(x)在(0，1)上是增函数，求实数a的取值范围；

(3)在第(2)小题的结论下，设g(x)=e2x+|ex-a|，x∈[0,ln3],求函数g(x)的最小值.

参考答案

1.D 2.B 3.A 4.B 5.D 6.B 7.D

8.C 9.C 10.B

依题意知函数f(x)的周期为3π，得

解得

于是

由x∈[0，π],得

即

因此f(x)的最小值为m，即m=0,从而

又∠C∈(0，π)，可得

于是

19.解(1)选取的5个福娃恰好组成完整“奥运吉祥物”的概率为

(2)ζ的取值为10，8，6，4，得

ζ的分布列如表2所示.

表2 ζ的分布列

因此

20.解(1)由点A，D分别是RB，RC的中点，可得

从而

∠PAD=∠RAD=∠RBC=90°.

又由PA⊥AD，及PA⊥AB,DA∩AB=A,得

PA⊥面ABCD，

因此

PA⊥BC.

由BC⊥AB,PA∩AB=A,得

BC⊥平面PAB.

又PB⊂平面PAB,得

BC⊥PB.

(2)取RD的中点F，连结AF，PF．由RA=AD=1,得

AF⊥RC.

又由第(1)小题知,PA⊥面ABCD，而RC⊂平面ABCD,于是PA⊥RC.又AF∩PA=A,从而RC⊥平面PAF,于是∠AFP是二面角A-CD-P的平面角.在Rt△RAD中,

在Rt△PAF中,

于是

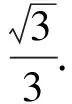
(2)定值为4.

(3)存在Q(0，0)，使得以MP为直径的圆恒过直线DP，MQ的交点.

22.解(1)当a=3时，

f(x)=x2+lnx-3x(x>0)，

从而

由f′(x)<0,得

2x2-3x+1<0,

解得

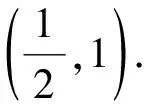
(2)由题意得

(3)当ex>a时,

当ex≤a时,