不等式恒成立问题分析与展望

● (西湖高级中学 浙江杭州 310002) ● (学军中学 浙江杭州 310012)

恒成立问题，因为其设问灵活，能够在考查思维的灵活性、创造性能力方面起到独特的作用，也有利于考查学生的综合解题能力，因此成了高考命题的一个热点.自2005年以来，尽管浙江省数学高考试题中的“恒成立问题”仅出了3道，但其特色明显、含义深刻.从题型上看，有选择题、填空题和压轴题;从数学思想方法来看，几乎囊括了函数与方程、化归与转化、数形结合以及分类讨论等.本文拟对不等式恒成立问题的一般题型和解题方法进行分析，并对未来可能出现的“恒成立问题”作出展望.

1 一般题型和解题方法分析

下面通过具体的例题全面介绍“不等式恒成立”问题的一般题型和解题方法.

例1已知对任意θ都有cos2θ-2msinθ-2m-2恒小于0，求m的取值范围.

解法1(函数最值分析法)设

y=cos2θ-2msinθ-2m-2=

-(sinθ+m)2+m2-2m-1.

因为-1≤sinθ≤1,所以考查函数的最小值:

(1)当-1≤m≤1时,得sinθ=-m，y的最大值为m2-2m-1.由m2-2m-1<0,得

于是

(2)当m>1时,得sinθ=-1，y的最大值为-2<0恒成立.

所以

即

例2某城市2001年末汽车保有量为30万辆，预计此后每年报废上一年末汽车保有量的6%，并且每年新增汽车数量相同.为了保护城市环境，要求该城市汽车保有量不超过60万辆，那么每年新增汽车数量应不超过多少辆？

略解设2001年末的汽车保有量为a1，以后每年末的汽车保有量依次为a2,a3…，每年新增汽车x万辆.由题意得

原题可转化为求当an≤60恒成立时x的取值范围.于是解得

右端是关于n的减函数.当n→+∞时，它趋于3.6，故要对一切自然数n满足an≤60，应有x≤3.6,即每年新增汽车应不超过3.6万辆.

例3设不等式2x-1>m(x2-1)对满足|m|≤2的一切实数m的取值都成立,求x的取值范围.

说明求解本题的关键是变换角度，以参数m作为自变量构造函数式，不等式问题变成函数在闭区间上的值域问题.本题有别于关于x的不等式2x-1>m(x2-1)的解集是[-2,2]时求m的值、关于x的不等式2x-1>m(x2-1)在[-2,2]上恒成立时求m的范围.

一般地，在一个含有多个变量的数学问题中，确定合适的变量和参数，从而揭示函数关系，使问题更明朗化.或者在含有参数的函数中，将函数自变量作为参数，而参数作为函数，更具有灵活性，从而巧妙地解决有关问题.

2 不等式恒成立问题热点命题展望

(1)数列与不等式结合是构造恒成立问题的热点.

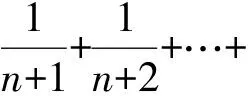
f(n+1)-f(n)=

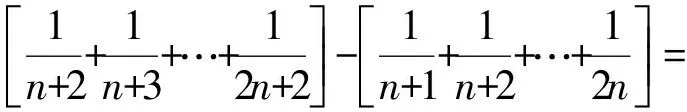
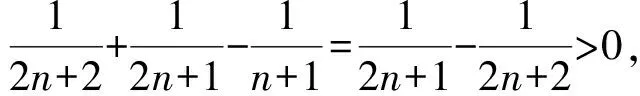
因此

f(n+1)>f(n).

解得

(2)含参数二次函数(三次函数的导数)在某一区间上恒成立问题或零点存在问题也是热点.

例5已知函数f(x)=x2+ax+3-a，在R上f(x)≥0恒成立，求a的取值范围.

解Δ=a2-4(3-a)=a2+4a-12≤0,

解得

-6≤a≤2.

变式1若当x∈[-2,2]时，f(x)≥0恒成立，求a的取值范围.

分析要使x∈[-2,2]，f(x)≥0恒成立，只需f(x)的最小值g(a)≥0即可,解得

-7≤a≤2.

变式2若当x∈[-2,2]时，f(x)≥2恒成立，求a的取值范围.

分析要证明f(x)≥2在[-2,2]上恒成立，若把2移到等号的左边，则把原题转化成左边二次函数在区间[-2,2]时恒大于等于0的问题.

解令g(x)=x2+ax+3-a-2≥0，

则原题可转化为求g(x)=x2+ax+1-a≥0在[-2,2]上恒成立的a的取值范围.

方法1(1)当Δ=a2-4(1-a)≤0时,解得

(2)当Δ=a2-4(1-a)>0时,得方程组

解得

方法2(运用根的分布)

g(a)=f(-2)=7-3a≥2,

解得

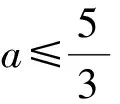
因此a不存在.

解得

因此

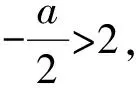
g(a)=f(2)=7+a≥2,

解得a≥-5,因此

-5≤a<-4.

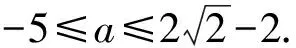
(3)把不等式进行合理的变形后，利用数形结合思想解题仍然是热点,这种方法对于选择题、填空题显得更灵活、快捷.

精题集粹

( )

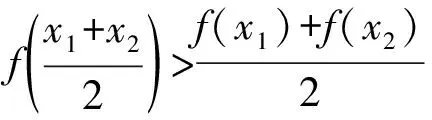
A.0 B.1 C.2 D.3

(2005年湖北省数学高考试题)

2.对于满足|a|≤2的所有实数a,求使不等式x2+ax+1>2a+x恒成立的x的取值范围______.

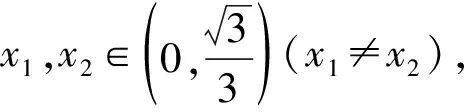
4．已知数列{an}的通项为an,前n项和为Sn，且an是Sn与2的等差中项，数列{bn}中,b1=1，点P(bn,bn+1)在直线x-y+2=0上.

(1)求数列{an}，{bn}的通项公式an,bn;

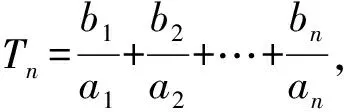
5．若函数

的定义域为R，求实数a的取值范围.

参考答案

1.B

2.(-∞,-1)∪(3,+∞) 3.-1≤a≤0

4.略解(1)an=2n,bn=2n-1.

(2)Bn=1+3+5+…+(2n-1)=n2，

故

(1)

(2)

式(1)-式(2)得

即

又

所以满足条件Tn

解得a=1.

(2)当a2-1≠0，即

时，有

解得

1

综上所述，f(x)的定义域为R时，a∈[1,9].