一类欠驱动Lagrangian系统的位置同步控制

周荻， 朱东方

(哈尔滨工业大学航天学院，黑龙江哈尔滨 150001)

0 引言

多运动轴或多驱动器间的运动同步问题，在现代制造工艺的发展过程中越来越多地引起人们的关注。Koren［1］首次提出了交叉耦合的概念解决运动同步问题。Rodriguez Angles等［2］采用一种反馈控制加非线性观测器的耦合同步控制策略实现了机械臂的位置同步控制。Sun Dong和 Liu 等［3－5］利用 Lyapunov 设计方法得到了一种自适应交叉耦合同步控制器，实现了多个机械臂的同步操纵和多个运动轴之间的同步运动控制。Shan Jinjun等［6］针对由多个三自由度直升机构成的系统设计了基于模型的交叉耦合同步控制器，取得了很好的同步效果。Sun Dong等［7］提出了一种无模型交叉耦合同步跟踪控制策略实现了多运动轴的位置同步。曹玲芝等［8］基于相邻交叉耦合对多感应电机设计了滑模同步控制器，该控制器具有很好的同步性和鲁棒性。以上研究成果中的被控对象均为全驱动系统，得到的相应控制策略无法直接挪用到欠驱动系统的同步控制问题中。

欠驱动系统是控制输入数目少于系统自由度的系统，即利用较少数目的控制量来实现系统的控制，在简化系统结构，降低系统复杂程度，节省能量和装置重量的方面，具有很大的优势。然而对于欠驱动系统的同步控制研究还较少，而且研究成果主要是针对具体的被控对象。Zhou Di等［9］分别采用同步误差积分引入线性二次型性能指标的方法和Backstepping方法，设计了开环和闭环操纵航天器回转运动时双转子控制力矩陀螺的同步控制律。Tsai等［10］针对并行双倒立摆同步运动系统在设计了两个子系统的稳定控制器后，设计了同步运动控制器，使两个子系统运动达到同步。本文针对一类欠驱动同步运动系统，研究其同步控制器的设计方法。

1 同步误差

考虑欠驱动同步运动系统由n个独立的欠驱动子系统构成，用qi代表第i个子系统的广义位置坐标。当第i个子系统跟踪指令信号qdi时，定义相应位置误差为ei=qi－qdi，i=1，2，…，n，可利用文献［3］中定义的同步函数求取相应的同步误差。同步误差反映了各子系统相应运动轴间的运动的不同步程度。对于同步误差也可以定义为一个子系统的运动轴与其相邻的子系统的相应运动轴间位置误差的线性组合［5］，写成矩阵的形式为

同步控制策略最终目标是达到e1=…=en=0，因此设计的控制器需保证位置误差e和同步误差ε均趋近于零。由位置误差和同步误差构造耦合位置误差为

其中:I为单位矩阵;α为选定的对角型正实增益矩阵。α的大小直接关系到同步控制效果的好坏，α越大系统的同步性能越好。由式(2)可知，当e*→0时，有e→0成立，进而由式(1)得到ε→0，此时系统具有较好的同步协调运动的瞬态性能。文献［3］中定义位置同步误差积分 与位置误差的和作为耦合位置误差，设计了同步运动系统的自适应同步控制器，虽然该控制器能够保证位置同步误差最终趋于零，但当耦合位置误差趋于零时，此时位置同步误差并不一定等于零，而系统有可能继续做协调运动，从而无法保证系统同步协调运动时的瞬态性能。

2 同步控制器

研究的一类欠驱动Lagrangian同步运动系统中子系统的动力学模型可统一描述，其中第i个子系统的动力学模型为［11］

其中:Mi(qi)表示系统的正实惯性矩阵;Ci(qi)代表科里奥利力和向心力的矩阵;Gi(qi)代表重力的矩阵，qi∈Rn代表系统的广义位置坐标，ui∈R为系统输入。由系统惯性矩阵Mi(qi)的正实性的性质，在式(3)两边均左乘(qi)整理可得

由式(5)可以得到系统(3)跟踪指令信号qdi时的误差状态方程为

其中

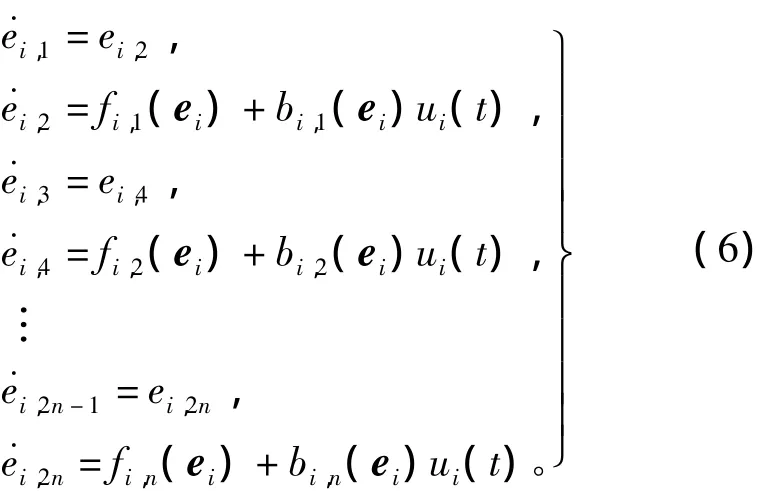
针对这一类欠驱动Lagrangian系统，Hao Yinxing等［12］采用了一种递阶滑模变结构控制策略设计了其鲁棒稳定控制器。这里采用递阶滑模变结构的思想设计同步控制器。根据式(2)耦合误差的构造方法，设计第一级滑模面

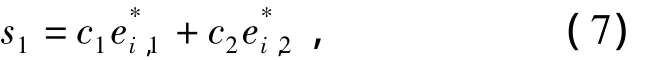
其中，c1和c2为符号相同的常数。

进而由第一层滑模面构造第二级滑模面

其中c3为常数。同样可以依次构造滑模面，直至系统的所有状态变量都包含在滑模面中。第j层滑模面为sj=cj+1+sj－1。在系统(6)中有 2n 个状态变量，所以其最后一级滑模面为s2n－1。

对系统(6)定义其Lyapunov函数

式(9)对t求导可得

根据式(10)设计系统的滑模控制器

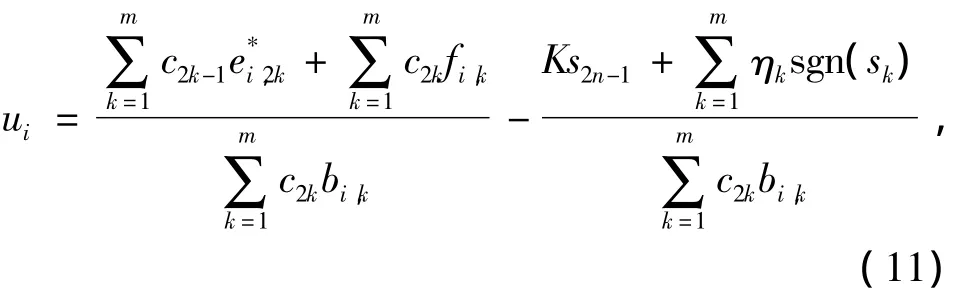
其中:K>0;ηk=2ηk－1;η1为正常数;

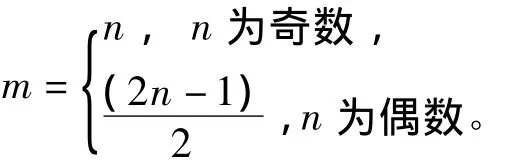
滑模控制律(11)保证系统满足到达条件，使系统的状态变量在滑模面上运动。当最后一层滑模面s2n－1趋近于零时，ui中包含 s2n－1的控制项消失，从而控制律(11)简化为滑模面s2n－2的等价控制和切换控制，进一步使s2n－2趋近于零，依次使沿着各层滑模面的运动完成，直到s1最终也趋近于零。

定理1 采用滑模控制律(11)时，系统(6)是渐近稳定的，且其位置误差以及同步误差渐近趋近于零，即当 t→∞ 时，ei→0 和 εi→0。

证明:对式(10)两边积分，并将式(11)代入得

根据ηk的定义可得

Vj(t)对t求导可得

由控制律(11)得

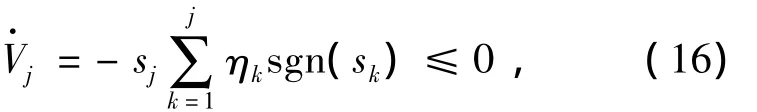
根据ηk的定义可得

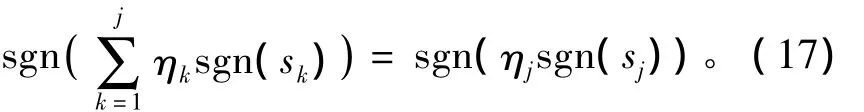
从而可进一步得到不等式

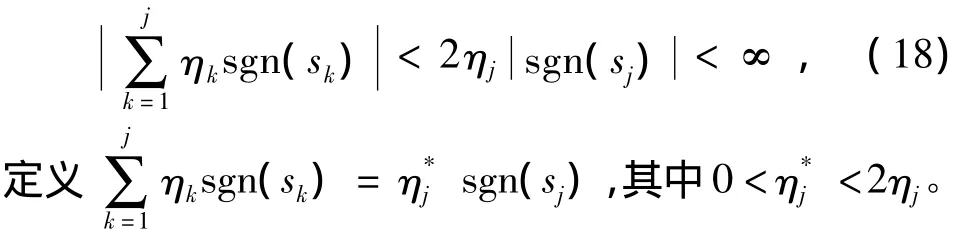
式(16)可以描述为

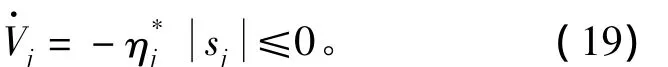
对式(19)两边积分可得

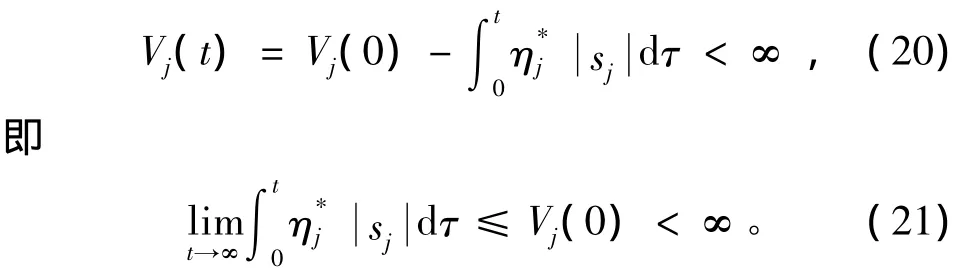
3 实例研究

3.1 两部倒立摆装置的同步控制实验

为了验证所设计的同步控制器的有效性，对由两部一级倒立摆装置构成的实际实验系统［10］进行了实时同步控制实验。对于一级倒立摆系统建立其数学模型为

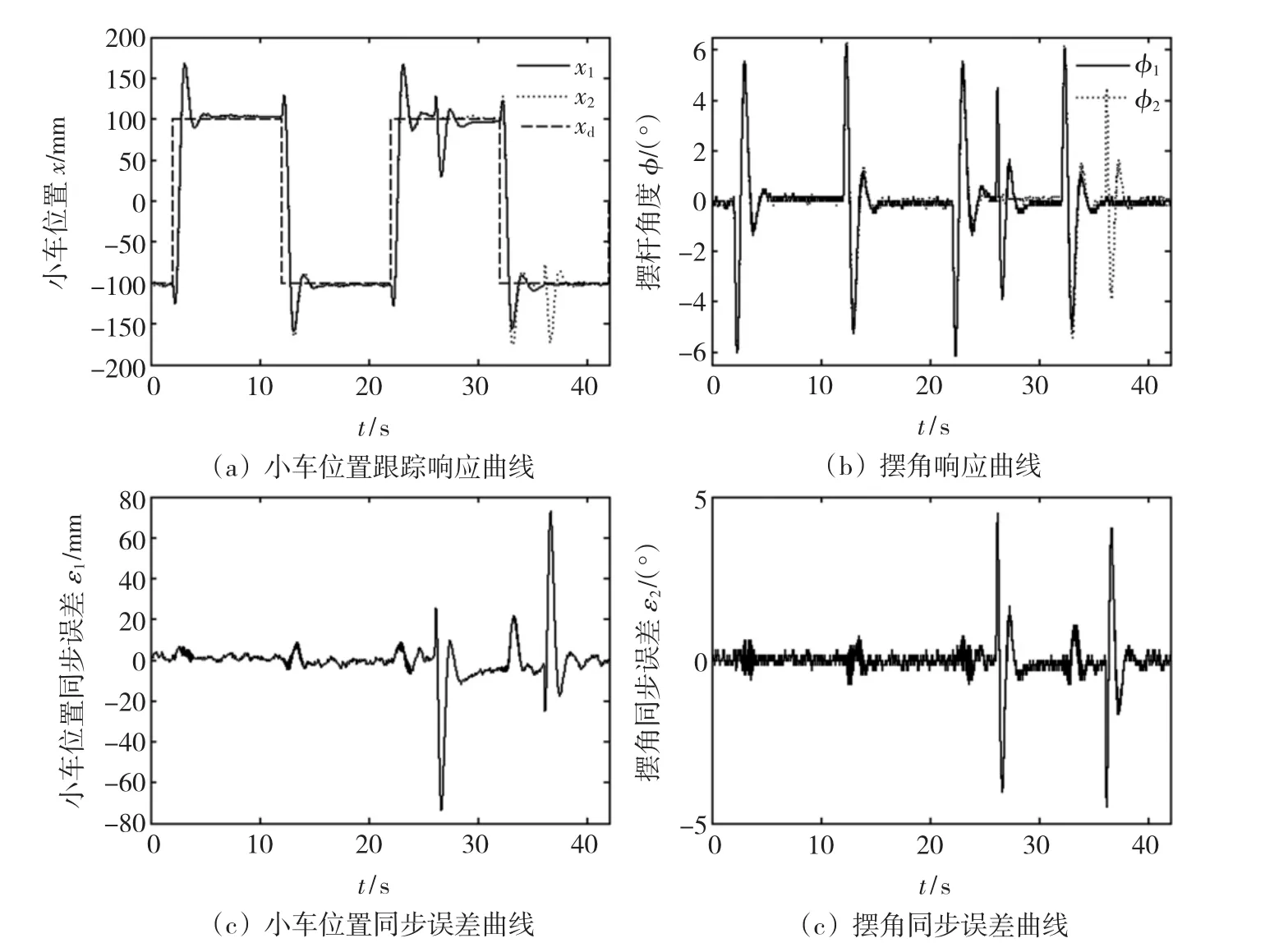
图1 未采用同步策略独立跟踪控制实验结果Fig.1 The experimental response without synchronization control scheme

其中:M为小车质量(M=1.37 kg);m为摆杆质量(m=0.107 kg);l为摆杆转动轴心到杆质心的长度(l=0.25 m);g为重力加速度(g=9.82 m/s2);u为加在小车上的作用力;x代表小车位置;φ代表摆杆与垂直向上方向的夹角。

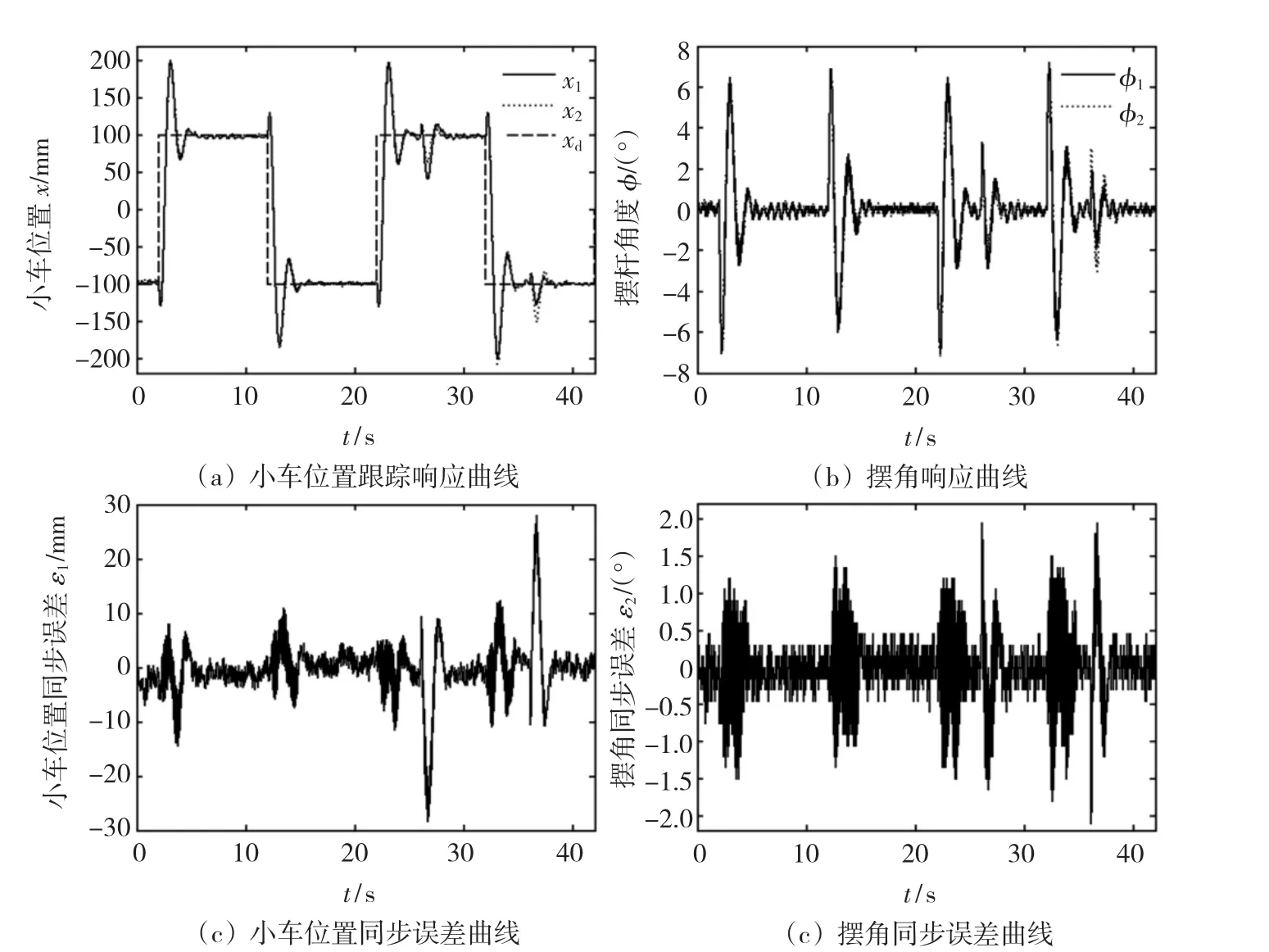
图2 采用比例耦合同步控制策略实验结果Fig.2 The experimental response with proportion coupling synchronization control scheme

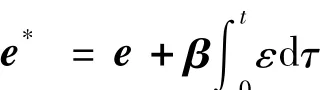
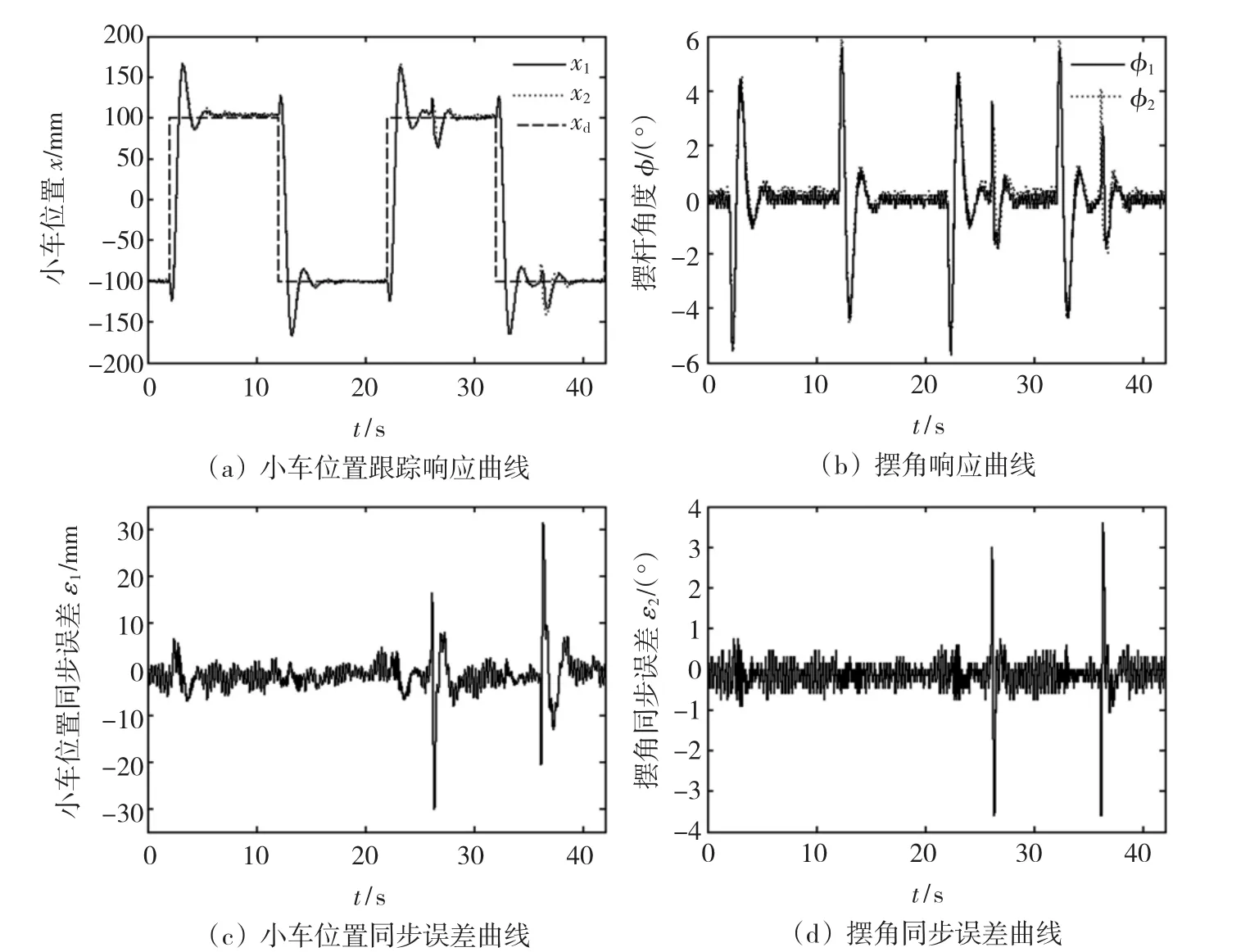
图3 采用积分耦合同步控制策略实验结果Fig.3 The experimental response with integral coupling synchronization control scheme

从图1可以看出，采用独立跟踪控制时虽然能够满足每个装置的跟踪性能，但存在较大的同步误差，小车位置同步误差峰值达73.7 mm，摆角同步误差峰值达4.5°。图2显示采用比例耦合同步控制器时同步运动系统不仅满足跟踪性能要求，而且具有较小的同步误差，小车位置同步误差峰值小于28.3 mm，摆角同步误差峰值小于2.1°。比较图2(c)～2(d)和图3(c)～3(d)可以看出，所设计的比例耦合同步控制器的同步性能优于积分耦合同步控制器的小车同步误差峰值31.4 mm和摆角同步误差峰值3.6°的性能。

3.2 4部倒立摆装置的同步控制仿真

进一步对4部倒立摆装置的同步运动系统进行同步控制研究，同步运动系统是由ADAMS软件搭建的虚拟物理模型。为了更接近实际物理模型，在小车和导轨之间加入摩擦力，其中静态摩擦系数设定为0.1 N·s/m，动态摩擦系数为0.05 N·s/m。小车的跟踪指令信号为幅值100 mm，周期为20 s的方波信号。根据2节同步控制器设计过程，结合倒立摆装置的结构参数，选取具体的参数为c1=－1.2，c2= － 1，c3=3.5，c4=1，K=0.5，η1=0.05，α=5I4(I4为单位矩阵)。为了测试系统性能，在15 s对倒立摆装置1的小车施加脉冲干扰。图4为采用独立跟踪控制时系统的仿真结果(α=0)。图5为采用本文所设计的比例耦合同步控制策略时的仿真结果。图6为采用积分耦合同步控制策略时的仿真结果，其中，β=10I4(I4为单位矩阵)。

图4显示采用独立跟踪控制时，系统的跟踪性能虽然可以满足，但无法保证整个系统的同步性能，小车位置同步误差峰值达143 mm，摆角同步误差峰值达6.2°。从图5可以看出，采用本文所设计的比例耦合同步控制器时，不仅保证了系统的跟踪性能，而且系统的同步性能也得到了改善，小车位置同步误差峰值小于39.3 mm，摆角同步误差峰值小于1.4°。比较图5(c)～5(d)和图6(c)～6(d)可以看出，比例耦合同步控制器的同步性能优于积分耦合同步控制器的小车同步误差峰值45.5 mm和摆角同步误差峰值5°的性能，同步协调运动的瞬态性能更好。

图4 未采用同步策略独立跟踪控制仿真结果Fig.4 The simulation result without synchronization control method

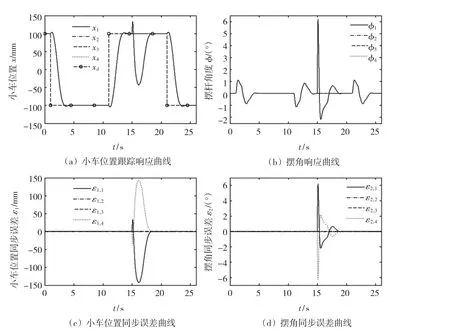
图5 采用比例耦合同步控制策略仿真结果Fig.5 The simulation result with proportion coupling synchronization control scheme

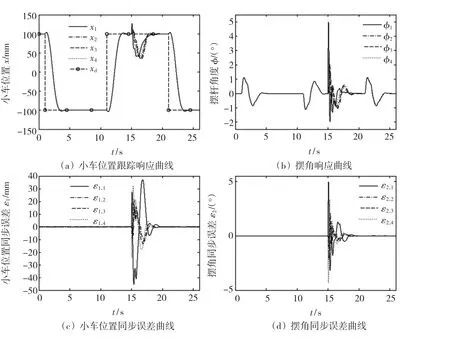
图6 采用积分耦合同步控制策略仿真结果Fig.6 The simulation result with integral coupling synchronization control scheme

4 结语

针对一类欠驱动Lagrangian系统定义位置误差加位置同步误差作为新的状态变量引入到递阶滑模控制器中，设计了一种交叉耦合位置同步控制器。所研究的同步控制器适用于多个(n≥2)单驱动输入欠驱动Lagrangian系统的同步控制。将该同步控制器应用到对由两部倒立摆装置的同步运动系统的实时控制实验和对由四部倒立摆装置的同步运动系统的仿真实验，均获得了满意的同步控制效果。所设计的同步控制器在控制同步运动系统时能达到很好的同步性能，且可保证系统对指令信号的精确跟踪，同时具有较强的抗干扰能力。

［1］KOREN Y.Cross-coupled biaxial computer controls for manufacturing systems［J］.ASME Journal of Dynamic Systems，Measurement，and Control，1980，102(2):256 － 272.

［2］RODRIGUEZ-ANGLES A，NIGMEIJER H.Mutual synchronization of robots via estimated state feedback:a cooperative approach［J］.IEEE Transactions on Control Systems Technology，2004，12(4):542－554.

［3］SUN Dong，MILLS J K.Adaptive synchronized control for coordination of multirobot assembly tasks［J］.IEEE Transactions on Robotics and Automation，2002，18(4):498－510.

［4］SUN Dong.Position synchronization of multiple motion axes with adaptive coupling control［J］.Automatica，2003，39:997 －1005.

［5］LIU H T，SUN Dong.Uniform synchronization in multi-axis motion control［C］//2005American Control Conference.Portland，OR，USA:ACC，2005:4537－4542.

［6］SHAN J，LIU H T，NOWOTNY S.Synchronised trajectory-tracking control of multiple 3-DOF experimental helicopters［J］.IEE Proc Control Theory Appl，2005，152(6):683 －692.

［7］SUN Dong，SHAO Xiaoyin，FENG Gang.A model-free cross-coupled control for position synchronization of multi－axis motions:Theory and Experiments［J］.IEEE Transactions on Control Systems Technology，2007，15(2):306－314.

［8］曹玲芝，李春文，牛超，等.基于相邻交叉耦合的多感应电机滑模同步控制［J］.电机与控制学报，2008，12(5):586－592.

CAO Lingzhi，LI Chunwen，NIU Chao，et al.Synchronized slidingmode control for multi-induction motors based on adjacent cross-coupling［J］.Electric Machines and Control，2008，12(5):586 －592.

［9］ZHOU D，SHEN T L，TAMURA K.Adaptive nonlinear synchronization control of twin-gyro precession［J］.ASME Journal of Dynamic Systems，Measurement，and Control，2006，128(3):592 －599.

［10］TSAI M C，SHEN B H.Synchronization control of parallel dual inverted pendulums driven by linear servomotors［J］.IET Control Theory Application，2007，1(1):320－327.

［11］SPONG Mark W.Partial feedback linearization of underactuated mechanical systems［C］//Proceedings of the IEEE/RSJ/GI International Conference on Intelligent Robots and Systems.Munich，Germany:IEEE，1994:314－321.

［12］HAO Yinxing，YI Jianqiang，ZHAO Dongbin，et al.Robust control using incremental sliding mode for underactuated systems with mismatched uncertainties［C］//2008American Control Conference.Washington，USA，2008:532－537.