离散伺服定位系统的复合非线性控制
2010-09-20程国扬彭可茂王惠
程国扬, 彭可茂, 王惠
(1.福州大学电气工程与自动化学院,福建福州 350108;2.新加坡国立大学Temasek实验室,新加坡 117508)
0 引言
伺服定位系统在工业加工和装配生产线中广泛存在。典型的伺服定位系统,要求系统的输出量能够快速、平稳且准确地进入目标位置的邻域,即系统同时具有良好的瞬态性能和稳态性能。为实现这个目标,需要引入反馈控制技术。目前已提出多种伺服控制方案[1],其中应用最广的为PID控制,包括常规的PID以及各种改进型 PID[2-3]。PID控制的优点是结构简单、容易实现,但由于它是一种单自由度结构的控制,其性能具有内在的局限性,难以兼顾系统快速响应与低超调之间的矛盾。
文献[4]提出一种基于线性反馈和非线性反馈的复合非线性反馈(composite nonlinear feedback,CNF)控制技术,其核心思想是通过加入非线性反馈来动态改变闭环极点的阻尼,以综合轻阻尼系统的快速响应性能和重阻尼系统的低超调特性,从而实现快速平稳的设定点跟踪。但文献[4]的CNF控制没有考虑扰动因素的影响,当系统中存在扰动时,CNF控制下的系统输出通常会有稳态误差。文献[5-6]分别提出在CNF中嵌入积分控制和扰动估计的方法来消除常值扰动的影响,从而实现准确的定位。文献[7]把CNF与近似时间最优控制结合起来,以实现大范围的准确定位。文献[4-7]的设计都是在连续时间域内,设计的控制器最终必须经过离散化后才能在实际系统上实现,这种模拟化设计通常要求一个30倍闭环带宽的离散采样频率,否则实际控制性能将出现较大的偏差,从而增加了设计和调试的工作量。在离散时间域上直接设计出数字控制器是一个更合理的选择。文献[8]给出了在离散时间域上带有积分控制的CNF设计方法。当扰动值或参考目标有所变化时,积分控制造成系统瞬态性能恶化,往往需要重新整定参数才能恢复系统原来的瞬态性能。
本文在离散域CNF设计的基础上,舍弃积分控制,采用一种扩展状态观测器来同时实现对系统未知状态和未知扰动的准确估计,并用于反馈控制和扰动补偿,以实现理想的伺服跟踪性能,其性能对给定目标和扰动值的变化不敏感,从而有利于实际应用和推广。
1 基于扰动观测的离散复合非线性控制
复合非线性反馈控制包含一个扰动观测和补偿机制,以消除伺服系统中由扰动引起的静态偏差。该方法保持了现有CNF控制方法的快速、平稳和准确的性能,同时还具有很好的性能鲁棒性,因而被称为鲁棒复合非线性反馈(robust composite nonlinear feedback,RCNF)控制。
典型的伺服控制系统是一个控制输入饱和受限的单输入单输出系统,数学模型为
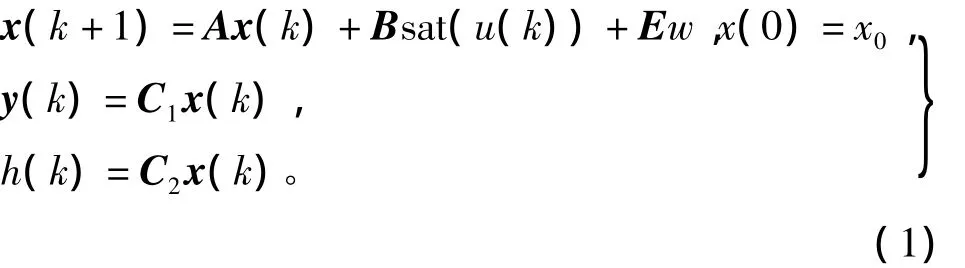
式中:x∈Rn;u∈R;y∈Rp,h∈R,w∈R 分别为状态变量、控制输入、测量输出、受控输出和扰动。A、B、C1、C2、E为定常矩阵。函数sat()为饱和限幅函数,定义为
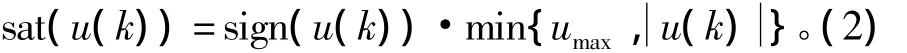
假设系统满足条件:
1)(A,B)可镇定;
2)(A,C1)能观;
3)(A,B,C2)可逆,并且在 z=1处无不变零点;
4)w是有界未知常值扰动;
5)h也是可测的,即它是测量输出的一部分。
上述条件是跟踪控制问题的标准假设条件。控制设计的目的是使带扰动的系统受控输出h能尽快平稳且无静差地跟踪参考输入信号r。
由于假设扰动是某个常值w,有

将式(3)加入系统模型中,得到增广系统为
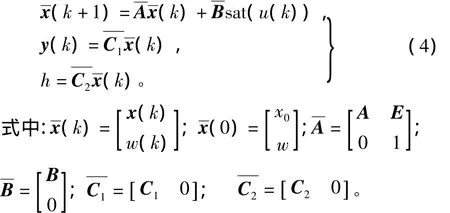
RCNF控制律的设计步骤为:①设计线性反馈律;②设计非线性反馈律;③设计观测器来估计不可量测的状态信号和未知常值扰动;④综合线性反馈、非线性反馈和观测器形成完整的控制律。
1)首先假设所有的状态变量和扰动都是可测量的。针对系统(1)设计一个带有扰动补偿的线性状态反馈控制律为
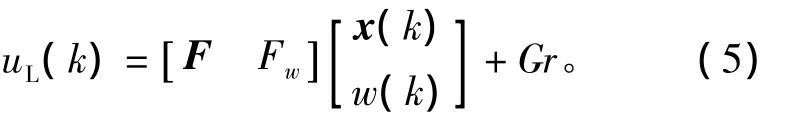
其中F的选取应满足以下条件:
1)A+BF渐近稳定;
2)闭环传递函数C2(zI-A-BF)-1B具有某种期望特性。
F的设计准则是使闭环系统具有一对主导极点,且其具有较小的阻尼比。这将使闭环系统具有快速的响应。G和Fw分别选择为
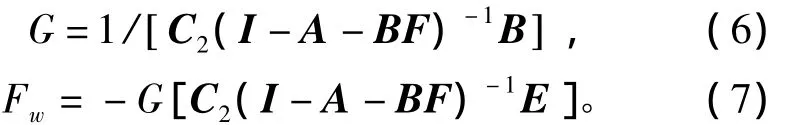
式(6)、式(7)中矩阵求逆的可行性是有保证的,因为已假设(A,B,C2)可逆且在z=1处无不变零点。式(6)、式(7)的取值可保证在线性控制律(5)的作用下,系统输出量h将渐近趋向于参考目标r。
2)选择一个正定矩阵W∈Rn×n,求解Lyapunov方程为

得到一个正定矩阵P,由于A+BF渐近稳定,此解总是存在的。
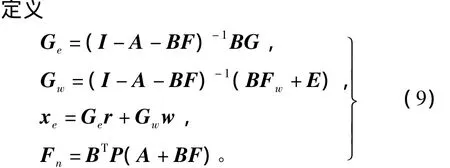
式中xe是系统状态向量x(k)的稳态目标值,且可以验证C2xe=r。RCNF的非线性反馈律为
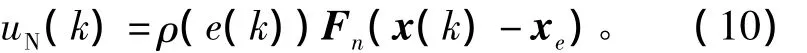
式中ρ(e(k))是误差e(k)=h(k)-r的非线性增益函数,用来逐渐改变闭环系统阻尼比,以得到一个较好的跟踪性能。
3)设计一个降阶观测器来估计不可量测的状态变量和未知的扰动。为简单起见,假设在系统(1)的测量输出矩阵为
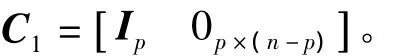
相应地,增广系统(4)可被分割为
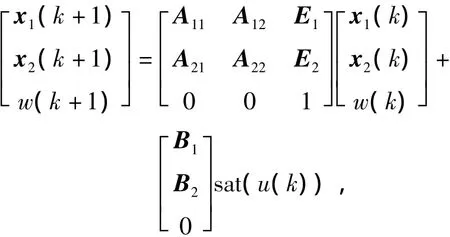
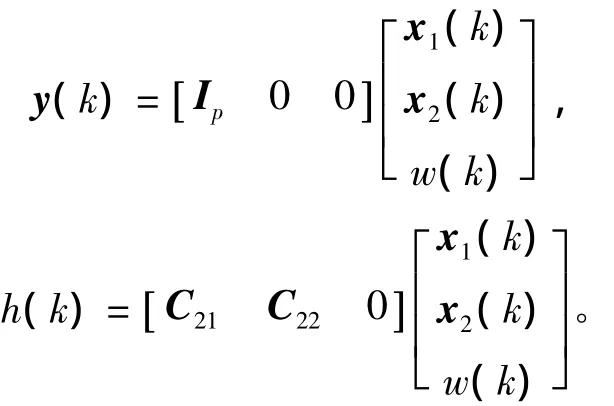
显然,x1即为测量输出y,所以仅需估计x2和w。
定义
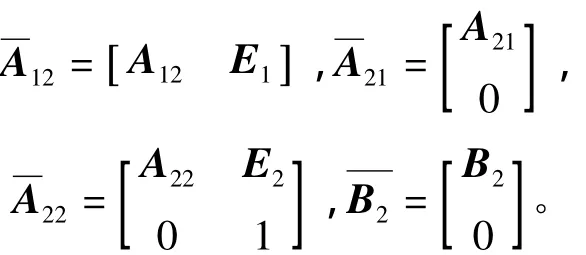
选择观测器增益矩阵K,将+K A12的特征值配置在z平面以原点为中心的单位圆内。
得到的降阶观测器方程[8]为
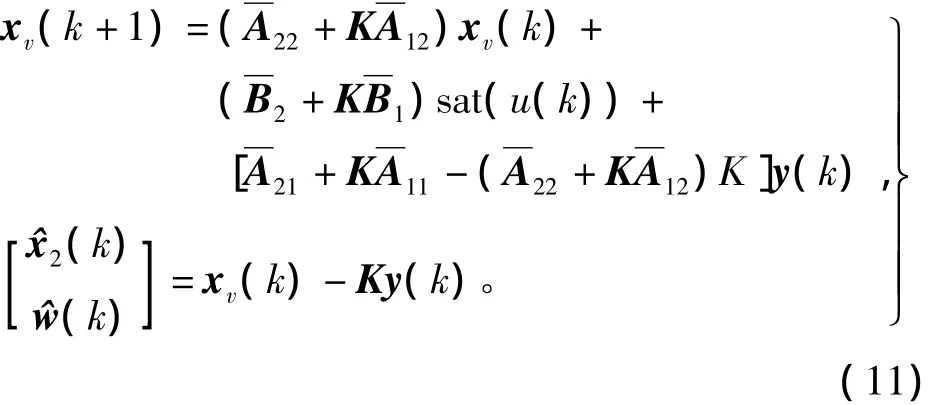
4)将线性反馈律、非线性反馈律和降阶观测器合并成最终的控制器,其中,不可量测的状态变量和未知扰动被各自的估计值代替。
基于观测器(11)的离散RCNF控制律为
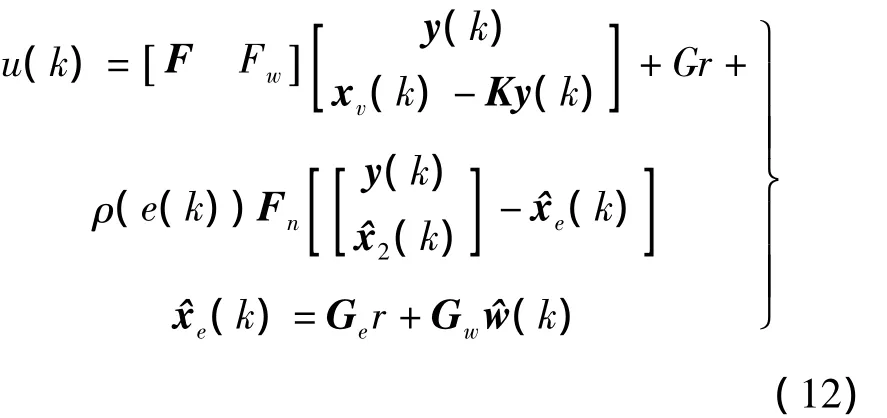
2 闭环系统稳定性分析
控制律(11)、(12)能解决系统(1)的定点跟踪问题。为便于推导,对反馈增益阵F和Fn进行分解,使其与x1和x2相一致,即

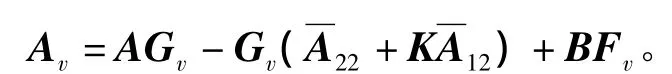
选取一个正定矩阵 WQ∈R(n-p+1)×(n-p+1),满足

求解关于正定矩阵Q的Lyapunov方程为

定理1 考虑式(1)给出的系统,其中未知扰动w的幅值以某个非负常数τw为界,即。在下列条件全部满足的情况下,存在一个常数ρ^>0,使得对于满足的任一平滑非正函数ρ(e(k)),由式(11)和式(12)构成的RCNF控制律能使系统的受控输出h(k)渐近无静差地跟踪定值参考目标r:
1)存在正常数δ∈(0,1)和cδ>0满足

为了表达简单,省略非线性函数ρ(e(k))的参数e(k),并且在不引起混淆的情况下省略时间索引(k)。
可验证式(20)成立,为

则系统的误差动态方程可表示为
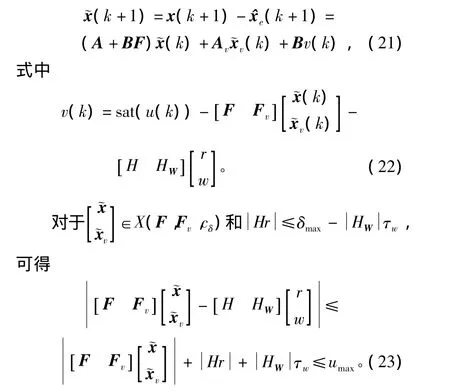
根据控制信号 u的幅值范围,由式(19)和式(22),v可以表示为
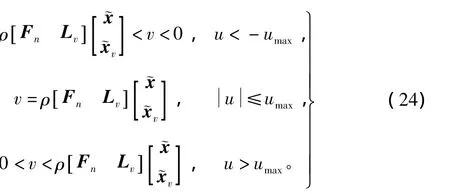
显然对所有可能的情况v均可以写为

需要证明当初始条件x0、xv0,参考目标r和扰动w满足定理中的限制条件时,误差动力学方程(26)是渐近稳定的。



即系统输出h(k)渐近无静差地跟踪参考目标r。
定理1证毕。
由式(26)的误差动力学方程可以看出:闭环系统的特征根可随ρ(e(k))和矩阵P而改变,而P由W阵来决定。通过合理选择W和ρ(e(k))的参数,可以调整控制律从而改进闭环系统的响应。总的来说,应选择一个合适的矩阵W>0阵和ρ(e(k)),以使得在稳态(e(k)=0)时闭环系统具有一对较大阻尼比的主导极点。这将有助于抑制系统输出响应的超调量。W的选择不是唯一的。一种可行的方法是把W阵限定为对角正定阵,并通过仿真来调整对角元素的值。
选取ρ(e(k))的一般准则是:它是关于e(k)的平滑非正函数,且 ρ(e(k))∈[-2/(BTPB),0]。一种可行的但不是唯一的选择为
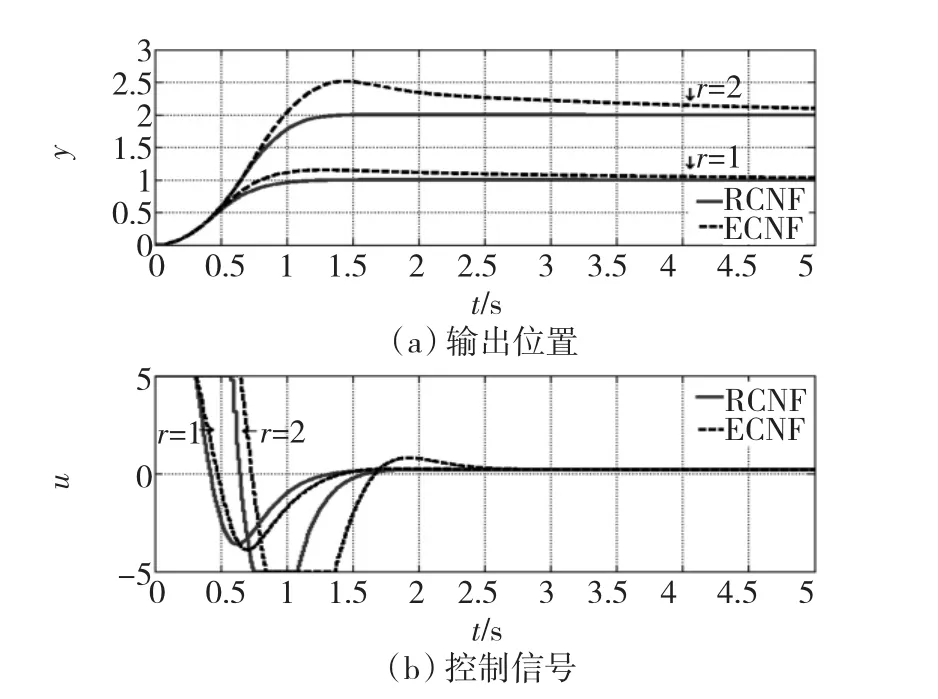
ρ(e(k))= -β/(BTPB)sech(α α0e(k)), (31)式中0≤α;0≤β≤2;sech()是双曲正割函数,sech(x)=2[exp(x)+exp(-x)],显然0 当h趋近于r时,ρ(e(k))将从-β/(BTPB)×sech(α)逐渐减小到 -β/(BTPB)。参数 α 可调节ρ(e(k))的变化率。 将系统模型按采样周期Ts=0.01s进行基于零阶保持器的离散化,得到如式(1)所示的离散状态空间模型,对应的系数矩阵为 选择一对闭环极点的阻尼比为0.4,自然频率为π,从而得到线性反馈控制律(5)中的参量为 由于 B=E,可知Fw= -1,Gw=0。 选取矩阵W为对角阵diag(100,1),得到非线性反馈律(10)中各矩阵为 非线性增益函数为 其中参数α0按式(32)计算。 将系统按式(4)增广后设计一个降阶观测器来估计状态变量和扰动信号。把观测器的极点按Butterworth模式配置,其截止频率选为采样频率的10%,得到观测器增益矩阵为 相应地,根据式(11)可得观测器方程为 最终的离散RCNF控制律为 为了进行比较,按照文献[8]提出的基于误差积分的增强复合非线性反馈(enhanced composite nonlinear feedback,ECNF)控制方案设计控制器为 RCNF控制器和ECNF控制器的控制信号需经过饱和限幅后才能进入系统的输入端。2个控制器都在r=0.1和w=-0.2的标称情况下进行参数整定,确保其具有优越的性能:2%调节时间为1 s,超调量很小。随后,分别改变参考目标r和扰动w的值,在Matlab/SIMULINK环境下进行仿真比较。仿真结果如图1~图3所示。可以看出:在各种条件下,2个控制器都能实现对参考目标的渐近无静差跟踪,即稳态误差为零,同时控制量u稳态趋向于扰动的相反值,刚好抵消扰动信号;但标称情况下具有良好性能的ECNF控制器对参考目标和扰动的变化非常敏感,其瞬态性能发生很明显的恶化;而RCNF控制器在各种目标或扰动值下的性能基本保持不变。图1中RCNF控制器在3种目标值下的调节时间都在1 s左右,无明显超调。图2中RCNF控制器在3种扰动值下的系统输出响应曲线几乎重合在一起。图3表明在控制信号饱和情况下(w=-0.2),RCNF控制器仍具有良好的性能,尽管其调节时间随参考目标的增大略有增加。综合以上结果,RCNF控制器可以在不同的扰动和目标值条件下正常工作,即其性能具有较好的鲁棒性。 图1 仿真结果(w=-0.2,r=0.05,0.1,0.2)Fig.1 Simulation results for w= -0.2 and r=0.05,0.1,0.2 图2 仿真结果(r=0.1,w=0.2,-0.2,-0.6)Fig.2 Simulation results for r=0.1 and w=0.2,-0.2,-0.6 图3 控制信号饱和时的仿真结果Fig.3 Simulation results in case of control saturation 本文提出了一种离散时间复合非线性反馈控制方案,用于实现快速和准确的定点跟踪。控制律以复合非线性反馈控制为主体,利用扩展状态观测器来估计系统状态和扰动信号并进行补偿。在一个典型的双积分伺服系统上进行仿真研究并与基于积分控制的CNF控制方案进行比较。结果表明:提出的控制方案可以实现快速、平稳和准确的伺服定位,且其性能具有更好的鲁棒性。进一步的研究工作将考虑时变的扰动信号。 [1]刘强.高性能机械伺服系统运动控制技术综述[J].电机与控制学报,2008,12(5):603-609. LIU Qiang.Survey on motion control technologies of high performance mechanical servo systems[J].Electric Machines and Control,2008,12(5):603-609. [2]ANG K H,CHONG G,LI Y.PID control system analysis,design,and technology[J].IEEE Transactions on Control Systems Technology,2005,13(4):559-576. [3]SERAJI H.A new class of nonlinear PID controllers with robotic applications[J].Journal of Robotic System,1998,15(3):161 -181. [4]CHEN B M,LEE T H,PENG K M,et al.Composite nonlinear feedback control for linear systems with input saturation:theory and an application[J].IEEE Transactions on Automatic Control,2003,48(3):427-439. [5]PENG K M,CHEN B M,CHENG G Y,et al.Modeling and compensation of nonlinearities and friction in a micro hard disk drive servo system with nonlinear feedback control[J].IEEE Transactions on Control Systems Technology,2005,13(5):708-721. [6]CHENG G Y,PENG K M.Robust composite nonlinear feedback control with application to a servo positioning system[J].IEEE Transactions on Industrial Electronics,2007,54(2):1132-1140. [7]程国扬,曾佳福.快速定位伺服系统的控制器设计[J].电机与控制学报,2009,13(1):52-56. CHENG Guoyang,ZENG Jiafu.Controller design for fast servo postioning systems[J].Electric Machines and Control,2009,13(1):52-56. [8]PENG K M,CHENG G Y,CHEN B M,et al.Improvement of transient performance in tracking control for discrete-time systems with input saturation and disturbances[J].IET-Control Theory&Applications,2007,1(1):65-74.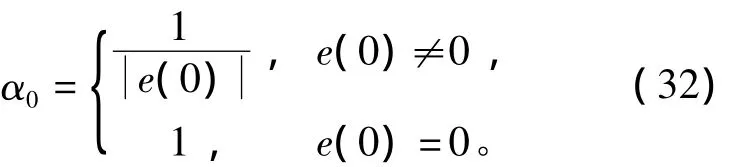
3 仿真研究
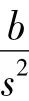
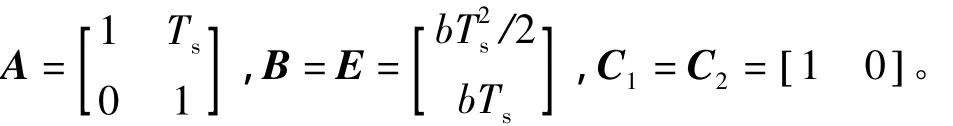
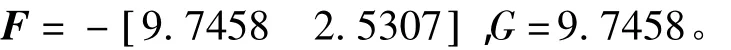

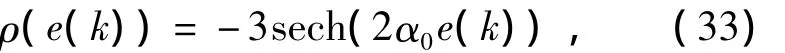
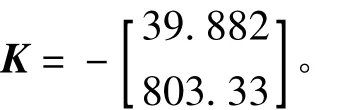
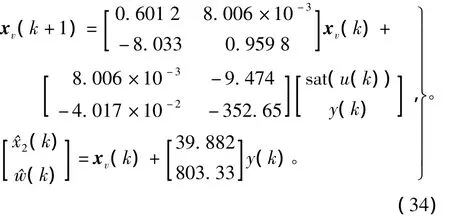

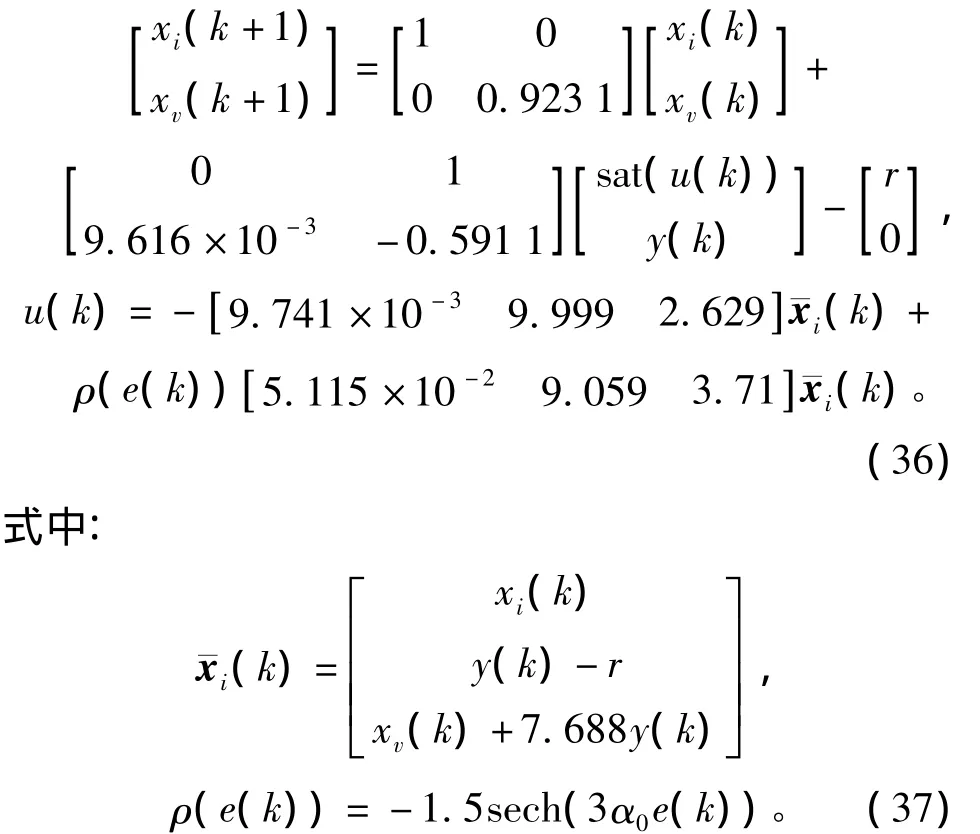


4 结语
