正弦电压馈电的直线感应发射器加速特性

杨宝峰， 李耀华， 严陆光

(1.中国科学院 电工研究所，北京 100190;2中国科学院研究生院，北京 100049)

0 引言

直线感应发射器(linear induction launcher)的基本工作原理与传统直线感应电机相同［1］，次级导体的感应电流在行波磁场的作用下产生电磁推力推动次级及其载荷沿发射器轴向运动。与传统直线感应电机不同的是发射器的工作过程始终没有进入稳态，电磁推力与速度一直处于动态变化过程中。建立直线感应发射器试验平台之前的必要准备工作之一便是预测其加速性能。

网孔矩阵法(mesh-matrix method)［2］或丝状电流法(current filament method)［3］是分析线圈型电磁发射器的经典数值算法，其共同思想是将初级和次级沿垂直于轴线方向的平面进行环形剖分，每个剖分出来的圆环内电流沿周向均匀分布，通过计算圆环的自感，圆环间的互感、互感梯度、电磁力，从而得出线圈型电磁发射器的等效电参数和电磁推力。国际上几家著名电磁发射研究机构根据这一思想，先后开发了自己的电磁发射仿真程序或软件［2－6］。

基于正弦稳态电流的分析模型［7］为直线感应发射器的设计提供了理论参考基础，但由于直线感应发射器一直处于瞬态运行模式，所以这种方法的预测结果与发射器特性会有很大的差距。鉴于直线感应发射器的主要馈电方式［8－12］，分析正弦电压激励的发射器特性则更具有代表性和普遍意义。本文以直线感应发射器的网孔矩阵方程为基础，分析了三相正弦电压触发时序、幅值、频率对直线感应发射器加速性能的影响。分析过程和结果为直线感应发射器的设计提供了理论参考。

1 直线感应发射器的物理模型与数值算法

1.1 基本结构与物理模型

直线感应发射器的基本几何结构如图1所示。发射器的初级由多个空心环型饼式线圈沿同一轴线排列构成;初级线圈内置套管，对初级线圈起保护作用，内膛作为次级的飞行轨道;次级为一般为圆柱型空心导体［4－5］。

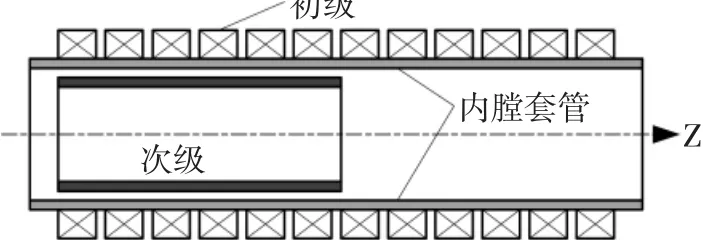
图1 直线感应发射器的结构示意Fig.1 Construction of the linear induction launcher

基于网孔矩阵法的直线感应发射器集中参数电路等效模型如图2所示。初级(驱动线圈，以字母d表示)和次级(弹丸线圈，以字母p表示)被沿垂直于轴线方向的平面进行环形剖分，每个剖分出来的圆环内电流沿周向均匀分布。实践表明，忽略线圈的螺旋性和电流的不均匀性的分析方法应用于轴对称线圈的磁场计算，不仅可以使计算工作量大为减轻，而且计算结果和实测数值之间仅有极小的误差［13］。

根据网孔矩阵法，直线感应发射器的电路及运动特性方程为

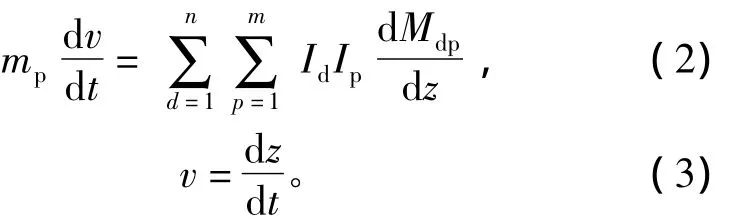
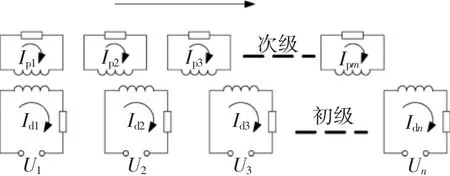
图2 直线感应发射器的集中参数等效电路模型Fig.2 Equivalent lumped parameter circuit for linear induction launcher

式中:

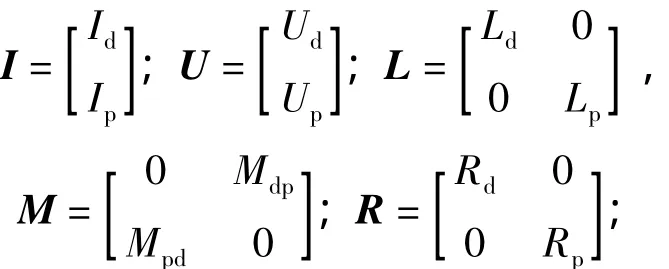
n和m表示线圈绕组的剖分单元数。I和U是两种线圈的电流和电压列矩阵，L和R是两种线圈自感和电阻对角矩阵，M是两种线圈互感方矩阵，dI/dt是电流对时间的变化率矩阵，dM/dt是两中线圈互感对空间的变化率矩阵。mp是次级的质量，v是次级的速度，z是次级的位移。

当以三相正弦电压激励直线感应发射器时，特性方程中的电压列向量矩阵为

1.2 电感计算方法

直线感应发射器基于网孔矩阵法的集中参数电路等效模型计算的核心工作是每个剖分单元自感及任意两个剖分单元之间互感的计算。

图3 网孔矩阵法剖分线圈Fig.3 Subdivision arrangement of coils for mesh-matrix method

对两同轴排列的耦合线圈进行如图3所示的环形剖分，则两个环形微元的互感

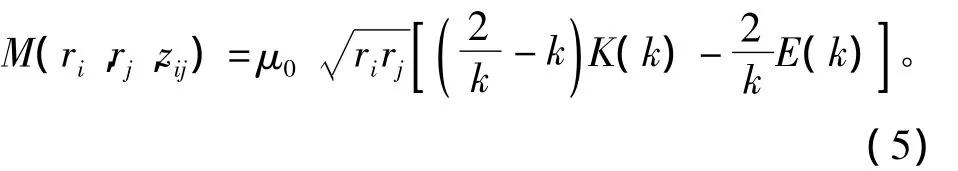
式中:ri和rj分别是两线圈第i和j个基本微元的半径;zij是这两个基本微元的轴向中心距离;k与他们的关系为

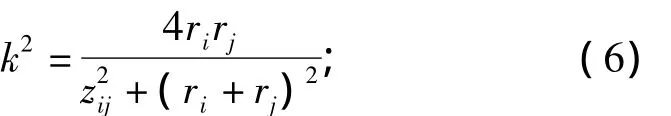
K(k)和E(k)分别是第一类和第二类完全椭圆积分，相应的表达式为

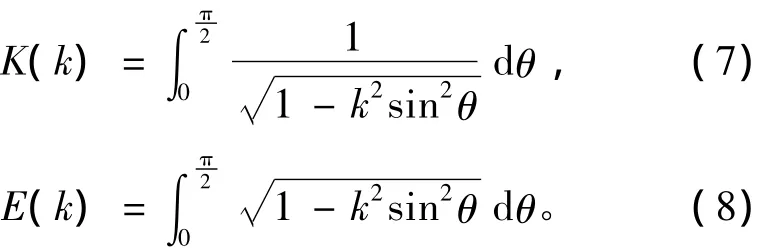
两微元的互感梯度表达式可由式(5)导出，即

对所有微元的互感及互感梯度求和，得到两线圈的互感及互感梯度

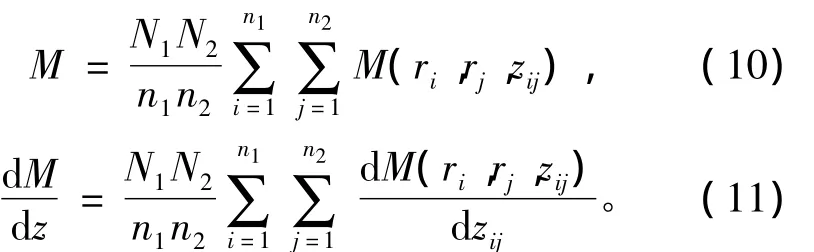
式中:N1和N2分别是两个线圈绕组的匝数;n1和n2分别是两个线圈的微元剖分数。

线圈的自感

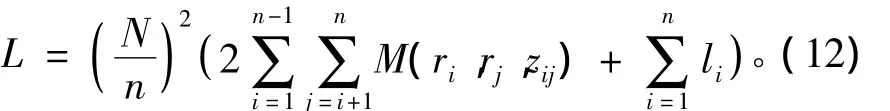
当剖分微元的横截面为正方形时，li的计算式［14］

式中:μ0为真空磁导率;ci、ai分别为第i个剖分微元线圈的径向厚度和平均半径。

2 直线感应发射器在三相正弦电压激励下的加速特性分析

仿真所选直线感应发射器的初级由24个空心饼式线圈同轴排列构成，每个饼式线圈的轴向长度为0.04 m，初级轴向总长度为0.96 m，采用三相供电的方式，每相8个线圈。初级极距为0.12 m，极对数为4。每个饼式线圈的绕线匝数为60，线圈等效半径为0.047 5 m。次级为圆柱型空心铝筒，等效半径为0.033，壁厚0.002 m，轴向长度0.24 m，质量0.274 8 kg，次级不携带其他负载。

2.1 电压初始相位对发射器性能的影响

取电压幅值Um=500 V，频率f=500 Hz，ω=2πf，初始相位角θ=0。次级从左向右的运动方向为正方向，如图1所示，次级左端面与初级左端面平齐的位置定为次级位移参考零点，则当次级初始位移为零时，初级绕组三相电流随时间变化的曲线见图4，为清晰起见，只给出了前5个周期的波形。

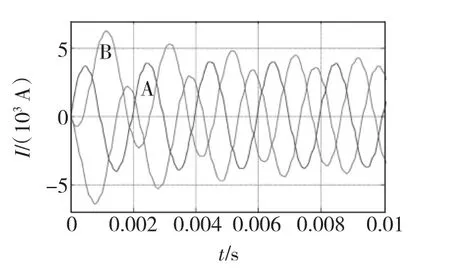
图4 初级绕组电流Fig.4 primary currents

图4中，三相电流不对称，在通电的最初几个电源周期内，B、C相电流有很大的直流分量。不对称的三相电流，可能会对次级产生与运动方向相反的制动力。初始相位角θ=0时的电磁推力与时间的关系曲线如图5所示。

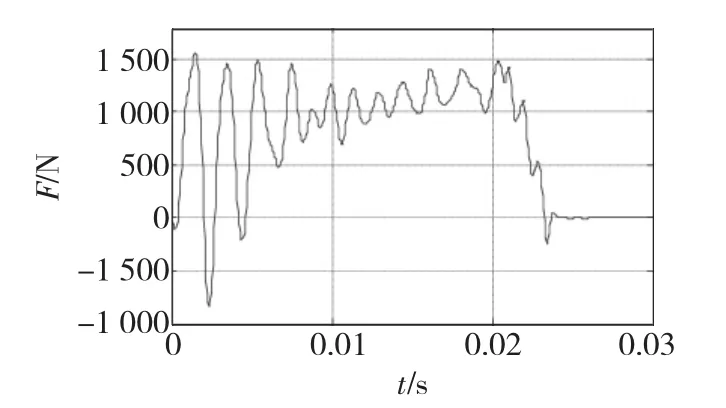
图5 电磁推力与时间的关系(Um=500 V，f=500 Hz)Fig.5 Propelling force vs time(Um=500 V，f=500 Hz)

三相电压的初始相位变化时，三相电流不对称性也随之变化，从而对发射器的加速过程产生不同的影响，导致次级的出膛速度的变化。次级出膛速度vm与三相电压初始相位的关系见图6。由图可知，在相同的电压作用下，存在使次级出膛速度最大的最佳电压初始相位。对于不同规模的加速器，电压初始相位对次级出膛速度的影响不同，对于选择的仿真模型参数，电压初始相位对次级出膛速度的影响并不明显。

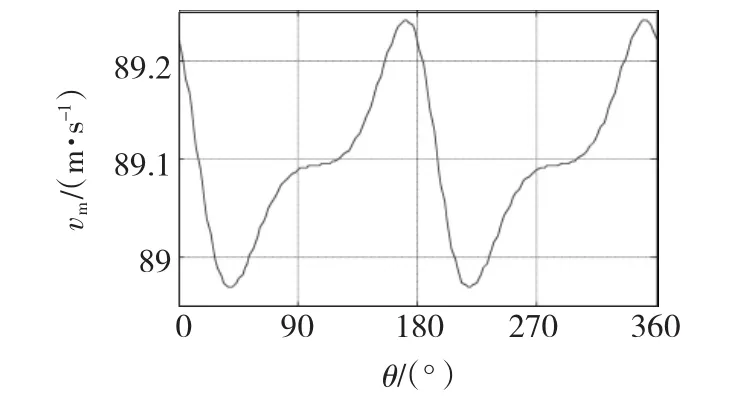
图6 出膛速度与电压相位角的关系Fig.6 Muzzle velocity vs phase angles

2.2 电压幅值对发射器性能的影响

取三相交流电压的频率为f=500 Hz，次级出膛速度与电压幅值的关系如图7所示。电压幅值小于600 V时，次级出膛速度随电压幅值的增大而提高;当电压幅值大于600 V时，次级出膛速度随电压幅值提高的速度明显变缓并出现波动，这是由于在次级即将出膛时，电磁推力迅速减小并出现负值，高电压幅值可能会产生更大的制动力。在电压幅值到750 V左右时，次级出膛速度已接近行波磁场的同步速度vs=120 m/s;电压幅值，次级的出膛速度将在行波磁场同步速度值以下小范围波动。如果希望次级出膛滑差控制在0.1～0.15，既出膛速度为102～108 m/s，则电压幅值取值范围为580～640 V。

图7 出膛速度与电压幅值的关系(f=500 Hz)Fig.7 Muzzle velocity vs voltage amplitudes(f=500 Hz)

图8示出了当电压幅值分别为600 V和800 V时的电磁推力与时间的关系。由图可见，电压幅值为800 V时，电磁推力作用时间短，电磁推力最大值接近600 V时的两倍，但次级出膛速度提高并不多。因此在次级出膛速度接近同步速度时，提高电压幅值只是对绕组的绝缘提出更高的要求、电磁推力的冲击值更高，而对提高次级出膛速度没有贡献。

2.3 电压频率对发射器性能的影响

取三相交流电压的幅值为Um=500 V，次级出膛速度与电压频率的关系如图9所示。当电压频率为430 Hz左右时，次级出膛速度达最大值96 m/s，此时的行波磁场同步速度vs=103 m/s，出膛滑差为0.068;当电压频率低于430 Hz时，次级出膛速度均比较接近于对应的行波磁场同步速度，不同的频率时，次级出膛时的电磁推力波动情况不同，所以出膛速度随电压频率值的增加而变化时的曲线并不十分光滑;当电压频率高于430 Hz时，次级出膛速度低于对应的行波磁场同步速度值较大，次级出膛时的电磁推力波动较小，出膛速度随电压频率值的增加而变化时的曲线比较光滑。

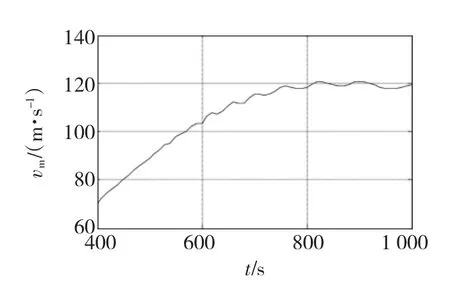
图8 电磁推力与时间的关系(f=500 Hz)Fig.8 Propelling force vs time(f=500 Hz)

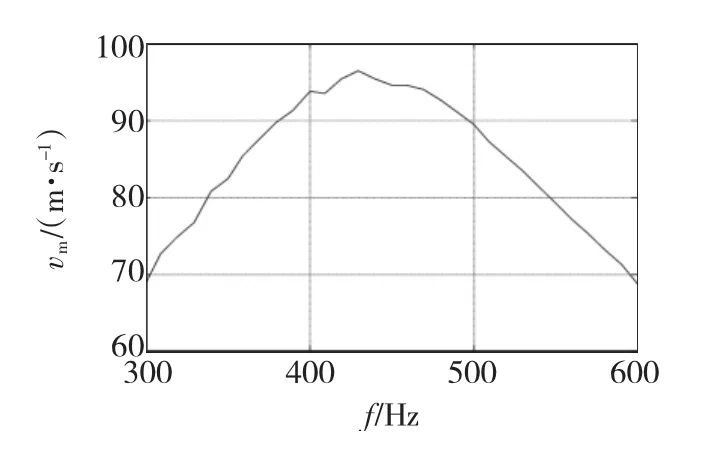
图9 出膛速度与电压频率的关系(Um=500 V)Fig.9 Muzzle velocity vs voltage frequencies(Um=500 V)

图10给出了电压频率为330 Hz、430 Hz、530 Hz时的电磁推力对时间的关系。电压频率为330 Hz时，电磁推力冲击值较大，次级速度很快接近磁行波的同步速度，电磁推力值迅速减小，并在次级即将出膛前后出现正负波动;电压频率为430 Hz时，电磁推力的冲击值小于330 Hz时的值，电磁推力作用时间长于330 Hz时的值，次级即将出膛前后电磁推力正负波动较小，次级出膛速度略小于磁行波的同步速度;电压频率为530 Hz时，电磁推力冲击值最小，作用时间最长，次级出膛速度远小于磁行波的同步速度。

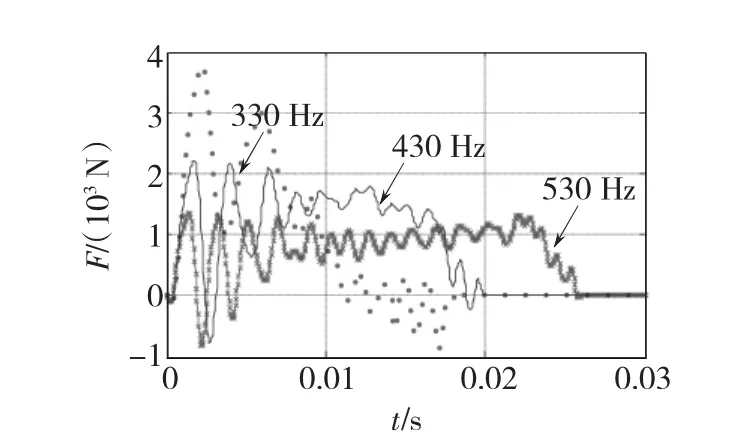
图10 电磁推力与时间的关系(Um=500 V)Fig.10 Propelling force vs time(Um=500 V)

由以上分析知，为使次级出膛速度最大，对于一定的电压幅值，有比较合理的电压频率值与之对应，过高和过低的电压频率都不利于发射器加速性能的充分发挥。

3 结语

本文讨论了直线感应发射器在三相正弦电压馈电方式下的加速特性。对于结构参数确定的直线感应发射器，为使次级获得最高的出膛速度，存在最佳电压初始相位;当电压频率给定时，应合理选择电压幅值，低电压幅值时次级出膛速度远低于对应的磁行波同步速度，过高的电压幅值需要更高的绕组绝缘等级，无益于提高出膛速度;当电压幅值给定时，存在最佳的频率值，过高和过低的电压频率都不利于发射器加速性能的充分发挥。

［1］ZABAR Z，NAOT Y，BIRENBAUM L，et al.Design and power conditioning for the coil－gun［J］.IEEE Transactions on Magnetics，1989，25(1):627 －631.

［2］ELLIOTT D G.Mesh-matrix analysis method for electromagnetic launchers［J］.IEEE Transactions on Magnetics，1989，25(1):164－169.

［3］WU A Y.Parameter studies for traveling wave coaxial launchers［J］.IEEE Transactions on Magnetics，1991，27(1):617 －622.

［4］WIDNER M M.WARP 10:a numerical simulation model for the cylindrical reconnection launcher［J］.IEEE Transactions on Magnetics，1991，27(1):634－638.

［5］ANDREWS J A，DEVINE J R.Armature design for coaxial induction launchers［J］.IEEE Transactions on Magnetics，1991，27(1):639－643.

［6］MARDER B.A coilgun design primer［J］.IEEE Transactions on Magnetics，1993，29(1):701 －705.

［7］HE J L，LEVI E，ZABAR Z，et al.Equivalent circuits and parameters for induction-type electromagnetic launchers［J］.IEEE Transactions on Magnetics，1993，29(1):696 －700.

［8］HE Jianliang，LEVI Enrico，ZABAR Zivan，et al.Concerning the design of capacitively driven induction coil guns［J］.IEEE Transactions on Plasma Science，1989，17(3):429－438.

［9］ZABAR Z，LU X N，LEVI E，et al.Experimental results and performance analysis of a 500 m/s linear induction launcher(LIL)［J］.IEEE Transactions on Magnetics，1995，31(1):522 －527.

［10］LIAO M，ZABAR Z，LEVI E，et al.Analysis of generator-drive linear induction launchers［J］.IEEE Transactions on Magnetics，1997，33(1):184－189.

［11］LIAO M，ZABAR Z，CZARKOWSKI D，et al.On the design of a coilgun as a rapid-Fire grenade launcher［J］.IEEE Transactions on Magnetics，1999，35(1):148－153.

［12］BALIKCI A，ZABAR Z，CZARKOWSKI D，et al.Flywheel motor/generator set as an energy source for coil launchers［J］.IEEE Transactions on Magnetics，2001，37(1):280 －283.

［13］雷银照.轴对称线圈磁场计算［M］.北京:中国计量出版社，1991.

［14］GROVER Frederick W.Inductance Calculations［M］.New York:Dover Publications Inc，1946.