数字谐振器在TACAN测位信号处理中的运用
2010-06-05胡健生
胡健生,付 涛
(1.武警工程学院,西安 710086;2.中国人民解放军95880部队,北京 100843)
0 引言
塔康系统(Tactical Air Navigation,TACAN)是一种近程导航系统,可以为飞机提供测距信息和测角信息,其中测距采用的是询问回答方式,而测角则是相位差式测角原理[1-3]。
塔康测角共分为粗测和精测两级,粗测采用的是15 Hz信号,精测采用的则是135 Hz信号,机载设备接收到的是二者的混合信号,在信号处理过程中需要将二者分开处理,而二者分离程度则直接影响系统的测角精度,因此,在数字化塔康接收机中需要采用较好的方法将信号分离。一般情况下,可以采用有限脉冲响应(Finite Impulse Response,FIR)滤波器来处理,并且用一种基于线性组合的处理方法[4],可以较好地达到所需结果,但这两种方法具体实现起来耗费资源较多且实时性不强,而考虑到数字谐振器作为单频滤出带通滤波器的良好滤波特性以及结构简单、实现方便、占用资源少的优点[5],选用数字谐振器来对信号进行处理是更优方案。
1 数字谐振器
有限脉冲响应(FIR)和无限脉冲响应(Infinite Impulse Response,IIR)结构都可以实现带通滤波功能[6-10],但是相比较而言,FIR结构的阶数往往较 IIR结构要多很多,在硬件实现中占用较多资源,延时较长,并且塔康测位信号带通滤波是两个频点的滤波,综合考虑结构、带宽等各种因素,在此选取数字谐振器作为滤波器。塔康机载设备信号处理框图如图1所示。

图1 塔康机载设备信号处理框图Fig.1 The diagram of signal processing in airborne TACAN
数字谐振器是二阶的IIR滤波器,是一类比较特殊的双极点带通滤波器,它具有一对共轭极点re±jw0,其中r近似于1。系统函数幅度特性在w=w0处取得最大值,相当于在w0处产生了谐振。由于这个特性,数字谐振器非常适合用作带通滤波器、语音发生器等。
数字谐振器的零点有两种放置方法,一种是取原点做零点,此时的系统函数为

其中:r越接近于1,极点就越接近单位圆,w0就越接近于谐振频率,谐振点的陡度就越大。它的3 dB带宽B≈2(1-r),b0取值使H(z)幅度最大值为1。
另一种是取±1为零点,系统函数为

同样r越接近于1,w0越接近于谐振频率,带宽 B≈2(1-r),b0取值使最大为1,但是此时谐振频率和带宽与取原点作为零点时略有不同了[4],稳定性更好。双零点数字谐振器的信号流程如图2所示。
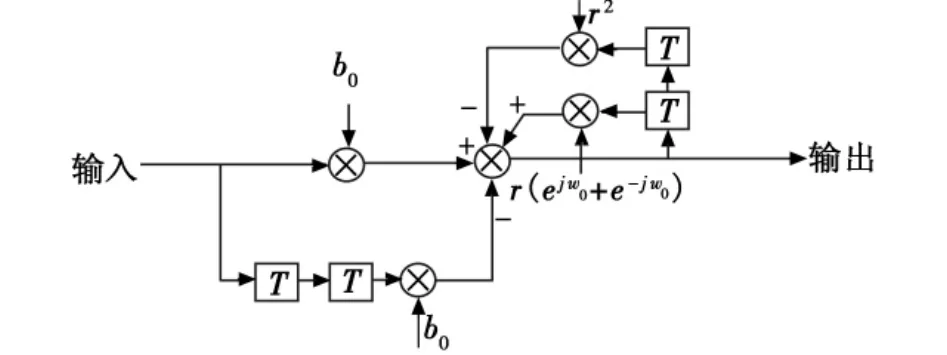
图2 双零点数字谐振器信号流程图Fig.2 Flow chart of the signal of the digital resonator with double zeros
2 数字谐振器设计
塔康测位信号包括方位基准信号和可变相位信号,其中可变相位信号中含有15 Hz的粗测信号和135 Hz的精测信号,而所要做的工作就是要使得这两个信号分开,以便测量角度,因此,针对这两个谐振频率需要设计两个数字谐振器分别进行滤波。
首先,对滤出15 Hz粗测信号的谐振器进行设计(系统的采样频率为40 kHz):选择双零点的谐振器模式,信号的数字频率为ω=15×2π/40000≈0.0023562 rad/s,把它作为谐振频率,数字带宽取为0.0005,即2(1-r)=0.0005,r=0.9995,将 z=eωj代入系统函数表达式,使幅度为1,得到b0≈0.00025。系统函数极点在单位圆内,系统稳定。谐振器的系统函数为
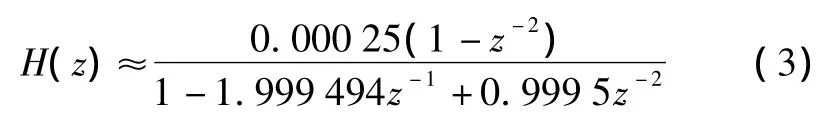
同样,135 Hz对应的数字谐振器也采用和15 Hz相同的设计方法,得到系统函数为

3 实验仿真
由于相位可变信号是以振幅调制方式调制在脉冲上的,所以又被称为方位包络信号,它的电相位随着塔康信标台磁方位角变化而变化,其表达式为
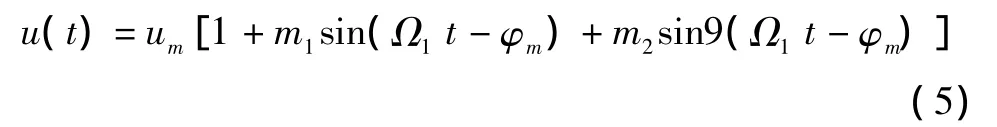
其中:um为振幅;Ω1=2πF1,F1=15 Hz;m1,m2分别是15 Hz和135 Hz包络信号调制度;φm为信标台磁方位角或15 Hz包络信号电相位角[1]。因此,假设信号为
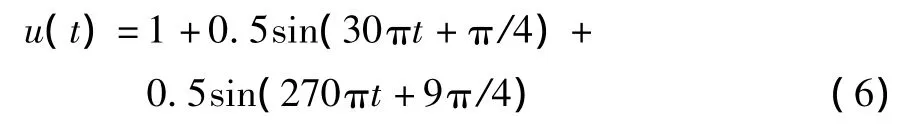
又考虑到在基准抑制和峰值检波可能引进其他的高频干扰,信号改为
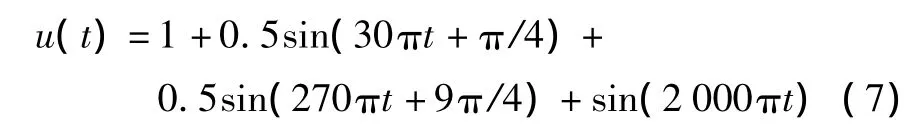
在Matlab中对谐振器的滤波性能进行仿真,将信号以40 kHz的采样率采样,再送至设计好的数字谐振器中,得到15 Hz滤波的波形和频谱图形分别如图3、图4所示。

图3 15 Hz信号滤波波形图Fig.3 The filtered wave of 15 Hz
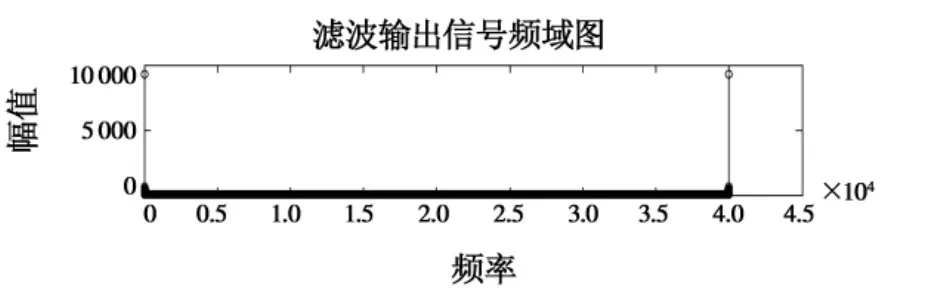
图4 15 Hz信号滤波频谱图Fig.4 The frequency spectrum of 15 Hz
135 Hz信号滤波的波形和频谱图形分别如图5、图6所示。
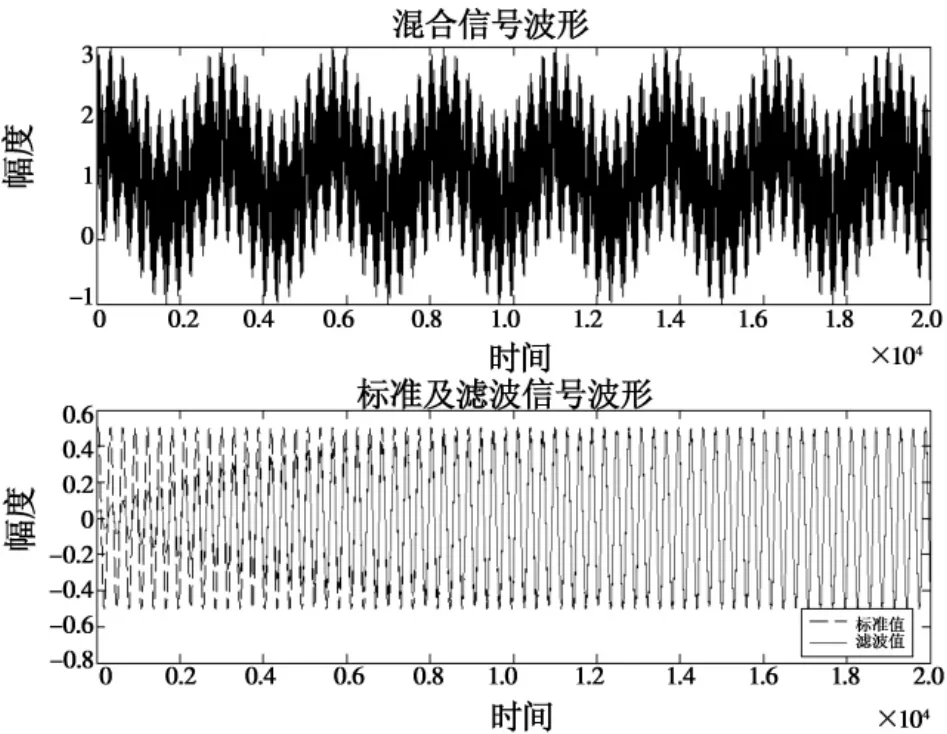
图5 135 Hz信号滤波波形图Fig.5 The filtered wave of 135 Hz
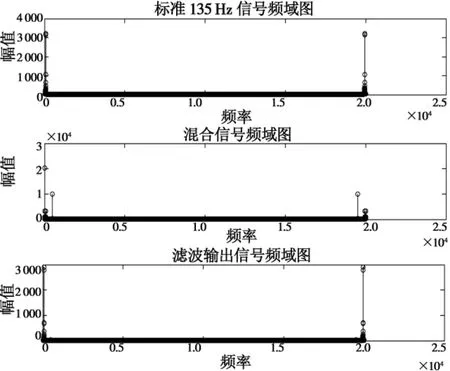
图6 135 Hz信号滤波频谱图Fig.6 The frequency spectrum of 135 Hz
从信号的波形上来看,输出信号经过短时的振荡就恢复到和原标准信号一致,混合信号中的其他频率分量被滤出了,而信号的频谱图也证实了这点,采用数字谐振器对塔康测位信号进行滤波取得了良好的效果。
4 结束语
数字谐振器是二阶的IIR结构的数字滤波器,相比较其他带通滤波器而言,它结构简单、易于实现、占用资源少、实时性强,具有在单频点上谐振的特性,这使得它适用于做单频带通滤波器。采用数字谐振器来对数字化塔康测位信号滤波,既节省了资源又保证了良好的滤波特性,通过实验仿真也可以证实这点。
[1]张忠兴,李晓明.无线电导航理论与系统[M].西安:陕西科学技术出版社,1998.
[2]江明.基于中频处理TACAN系统设计与实现[D].西安:西安电子科技大学,2007:5-9.
[3]岳鹏,孙国忠.陆基航空导航系统应用现状与技术发展[J].直升机技术,2002(1):46-49.
[4]王玉林,李艳斌.基于线性组合的塔康方位信号处理[J].信号与信息处理,2006,36(11):38-40.
[5]方艳梅.数字信号处理[M].北京:电子工业出版社,2007.
[6]周辉.3型FIR滤波器优化设计研究[J].系统工程与电子技术,2004,26(12):1893-1904.
[7]袁琼清,李彦鹏.基于Kalman自适应滤波器的噪声消除器设计研究[J].电光与控制,2004,11(3):50-53.
[8]赵亚梅,杜红棉,张志杰.基于MATLAB一种IIR数字带通滤波器的设计与仿真[J].微计算机信息,2007,23(5):233-285.
[9]张葛祥,金炜东,胡来招.一种有效的IIR数字滤波器优化设计方法[J].信号处理,2004,20(2):152-156.
[10]高西全,丁玉美.数字信号处理[M].北京:电子工业出版社,2000.
