基于粒子群算法的总能量飞控系统优化设计
2010-06-05李冀鑫侯志强
李冀鑫,侯志强
(1.海军飞行学院教研部,辽宁 葫芦岛 125001;2.海军航空工程学院,山东 烟台 264001)
0 引言
舰载飞机为了能够安全着舰,在下滑阶段不但要抗击舰尾气流扰动,而且要跟踪甲板随海浪的随机运动。这对着舰的航迹控制提出了较高的要求。然而,舰载飞机在着舰下滑阶段处于一种低动压的空气动力状态[1],航迹角和速度之间强烈耦合,单独依靠升降舵无法精确控制飞行航迹。文献[1]深入分析了造成这种现象的原因,指出只有设计动力补偿系统,才能解除航迹角和速度之间的强耦合,实现航迹的精确控制。目前,一些学者采用各种控制理论设计综合着舰飞行/推力控制系统,但是有些控制算法(例如H∞理论设计的控制器)由于太复杂而不实用[2];有的控制算法虽然简单,性能却不理想。因此,为获得精确的着舰航迹控制效果,研究一种工程实用的控制方法是亟待解决的问题。
飞机总能量控制系统(Total Energy Control System,TECS)[3]是在20 世纪 80 年代由 Boeing公司提出的。总能量控制系统作为一种全新的综合飞行/推力控制系统,具有结构简单和鲁棒性强的特点,已经在飞行控制领域显示出广阔的应用前景[4-5]。
但是,总能量控制系统需要整定的参数较多,依靠人工试凑难以得到最佳的控制效果。目前,优化理论的发展为控制器的参数整定提供了一种有效的途径。其中,粒子群优化算法[6](Particle Swarm Optimization,PSO)作为一种并行优化算法,具有运算简单和易于实现的特点,已经广泛应用于科学和工程领域[7-8]。
为此,本文提出了基于粒子群优化算法的总能量着舰飞行控制系统设计方法,对总能量控制系统的参数进行优化。频域分析和时域仿真结果表明,所设计的控制器简单易行,并且具有良好的控制性能。
1 总能量控制系统基本理论
飞机飞行时的总能量可表示如下:
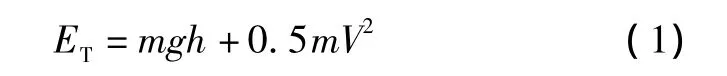
式中:ET为飞机总能量,由势能和动能组成;m为质量;g为重力加速度;V为飞行速度;h为飞行高度。
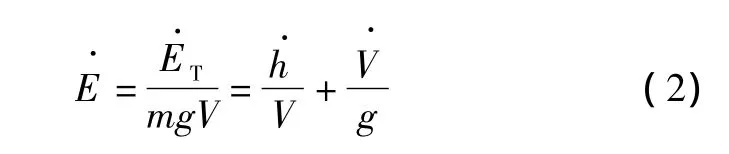

飞机质心运动的切向力方程可表示为
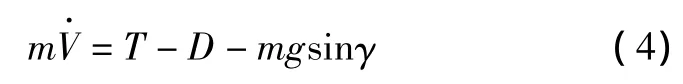
式中:T为发动机推力;γ为航迹角;D为气动阻力。对上式进行整理可得:
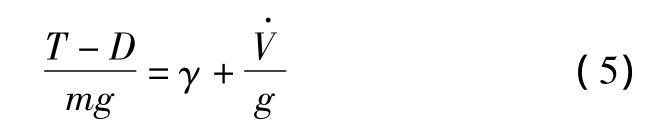
式(3)和式(5)揭示了这样的事实:发动机推力可以改变飞机的总能量变化率。实际上,经典的总能量控制理论认为,在飞行中飞机的气动阻力保持不变,所以改变飞行状态所需要的推力增量ΔT为
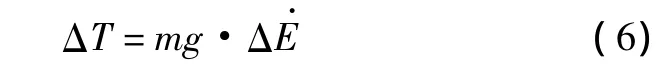
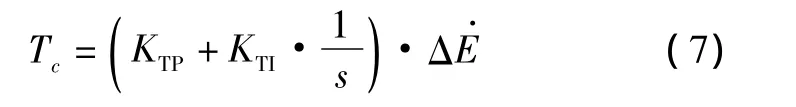
式中:Tc为改变飞行状态所需要的发动机推力;KTP为比例系数;KTI为积分系数。该控制律的作用是使得由于飞行状态改变引起的总能量变化率的偏差Δ趋于零。
总能量变化率描述了飞机势能和动能总的变化趋势。为了描述两者之间的比例关系,定义总能量的分配率如下:

能量分配率可以由飞机的升降舵进行控制,可以近似认为升降舵的偏转不改变飞机的总能量,只是通过俯仰姿态回路将飞机的动能和势能相互转换。综合考虑改善飞机短周期运动品质所需要的阻尼项,采用类似于推力的控制律表示升降舵偏转角的控制量为
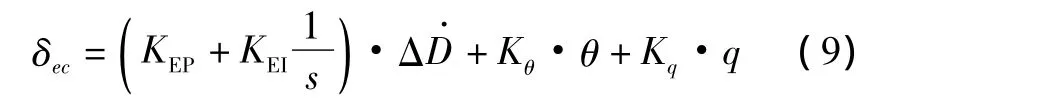
式中:δec为改变飞行状态所需要的升降舵偏转角;KEP为比例系数;KEI为积分系数;为期望的总能量分配率和实际的能量分配率之差,即;Kθ和Kq分别为俯仰角和俯仰角速度的反馈增益。该控制律的作用是使能量分配率的偏差趋于零,同时改善飞机短周期运动的品质。
式(7)和式(9)构成了总能量控制系统的核心算法。值得说明的是,经典的总能量控制理论在式(7)和式(9)中的比例控制部分采用飞机实际的能量变化率和分配率代替偏差信号,其理由是为了防止系统中不期望的零点引起响应的超调。但是,系统的超调和快速性是对立统一的,它们是同一矛盾的两个方面。可以充分利用超调带来的系统响应的快速性,而超调量则可以通过对参数的优化使之限制在允许的范围之内。基于总能量控制理论的飞控系统结构如图1所示。可见,该飞控系统需要优化的参数为KTP,KTI,KEP,KEI。
总能量控制系统要求的输入是航迹角指令γc和切向加速度指令c/g。几乎所有的纵向飞行控制模态都可以转化为该指令。比如舰载飞机的着舰飞行控制系统,其目标就是在保持飞行速度不变的条件下,实现航迹角的精确控制。可以用下式得到切向加速度指令。
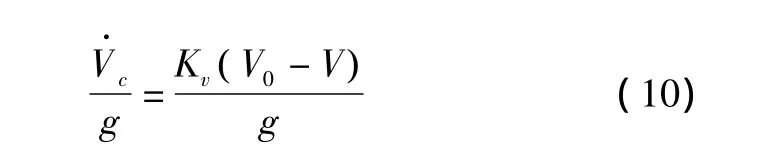
式中:V0是要保持的速度恒定值;V是实际飞行速度;Kv是速度增益,本文设定为1.5。
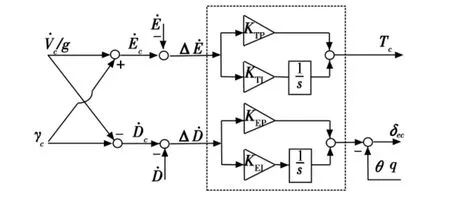
图1 总能量控制系统Fig.1 Total energy control system
2 粒子群优化算法
粒子群优化算法中的每个粒子都代表一个可能的解。粒子在迭代过程中通过跟踪自身找到的最优解和群体找到的最优解这两个极值来更新自己。PSO算法的基本原理可以描述如下[6]:设总粒子数为m,搜索空间维数为D。第i个粒子的位置和速度分别表示为xi=(xi1,xi2,…,xiD)和 vi=(vi1,vi2,…,viD);第 i个粒子找到的历史最优点为 pi=(pi1,pi2,…,piD);群体内所有粒子找到的历史最优点为pg=(pg1,pg2,…,pgD)。每个粒子按如下方程进行速度和位置更新:
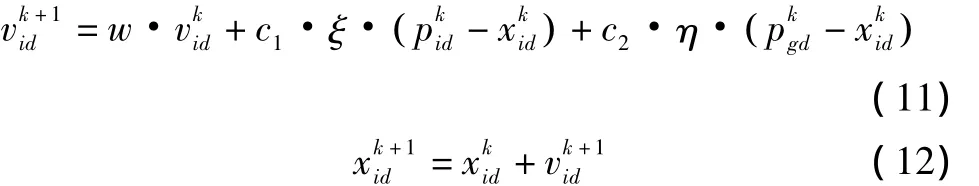
式中:i=1,2,…,m;d=1,2,…,D;d 表示粒子的第 d维坐标;k表示粒子群算法迭代的次数;c1和c2是学习因子,其作用是使粒子具有自我总结和向群体中优秀个体学习的能力;ξ和η为[0,1]之间的伪随机数;w称为惯性权重,它使粒子的运动保持惯性。
3 基于PSO的TECS参数优化
3.1 数学模型与阻尼器参数选择
数学模型是控制律设计和仿真的基础。文献[2]提供了大黄蜂舰载飞机近舰着舰状态下的线性化模型,整理后的系统状态方程为
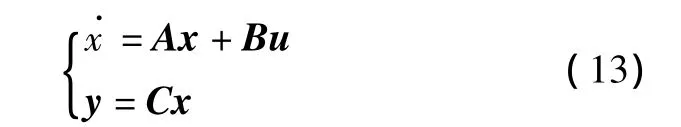
式中:x=(V,α,θ,q)T;u=(δeδp)T;y=(V,γ)T;V 是飞行速度;α是迎角;θ是俯仰角;q是俯仰角速度;δe是升降舵偏转角;δp是油门杆偏转角;γ是航迹角。方程中的矩阵分别如下:

总能量变化率和分配率可以根据式(3)和式(8)由系统状态方程引出。描述发动机和升降舵执行机构动态特性的数学模型详见文献[2]。
分析自然飞机的线性化数学模型发现其短周期阻尼仅为0.277,而一级飞行品质要求短周期阻尼应该在0.35 和1.30 之间[9]。为此,式(9)把俯仰角和俯仰角速度反馈到升降舵形成阻尼器。经研究取反馈增益为 Kq=1,Kθ=0.4,则系统的短周期阻尼为 0.768,满足了一级飞行品质的要求。
3.2 适应度函数的选择
在这里适应度函数就是评价控制系统性能的指标。众所周知,一个设计良好的控制系统对于阶跃输入的响应具有较短的上升时间和尽量小的稳态误差。本文采用时间的平方乘以阶跃响应误差绝对值的积分作为系统响应速度的性能指标,即:
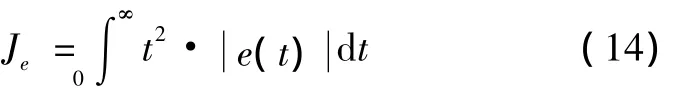
为了最大限度地使航迹角和速度解耦,采用下式作为衡量航迹角/空速耦合程度的指标。
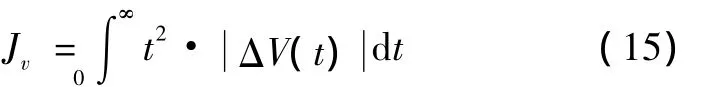
式中:ΔV(t)是航迹角跟踪阶跃输入时引起的速度变化量。
综合考虑航迹角阶跃响应性能指标和航迹角/空速耦合指标,采用权重系数法得到一个综合的性能指标作为粒子的适应度函数。
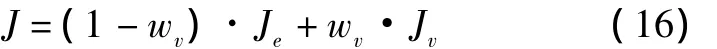
式中:wv为权重系数,本文设定wv=0.1。
3.3 PSO-TECS 算法流程
确定适应度函数以后,就可以编写程序对参数进行寻优。PSO算法的具体步骤如下:
1)初始化相关参数,包括粒子群大小、搜索空间维数以及各粒子的位置向量和速度向量等;
2)以各粒子的位置向量元素作为控制器参数进行仿真,并根据式(16)计算其适应度函数值;
3)将各粒子的适应度函数值与pi和pg进行比较,并更新之;
4)按式(11)和式(12)更新粒子的速度向量和位置向量;
5)若迭代次数未达到最大设定值,则返回2);否则,优化结束,输出最终的pg,即控制器的优化参数。
3.4 优化过程与结果
首先,在Matlab/Simulink中建立基于总能量控制系统的着舰飞控系统仿真模型。然后,在Matlab编程环境下编写粒子群优化程序。在计算各粒子适应度函数的时候调用总能量飞控系统的Simulink模型进行仿真。
粒子群种数设为20,最大迭代次数为100。学习因子均取为2。粒子最大速度均设为0.8。各个待优化参数的取值范围均设为[0.014]。
在优化中发现惯性权重的大小对算法的搜索能力和收敛速度有很大影响。较小的惯性权重有利于算法尽快收敛,而较大的惯性权重有利于增加粒子在解空间的搜索能力。为平衡这两方面的要求根据式(17)调节惯性权重,即在前50次迭代中线性地减少惯性权重,而在以后的迭代中采用固定的惯性权重。
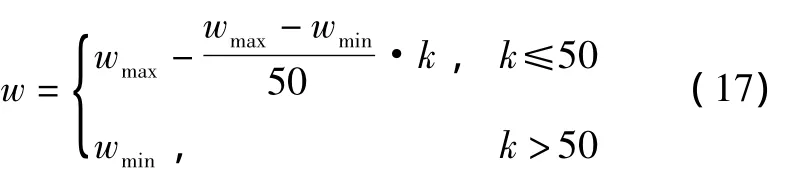
式中:k为迭代次数;wmax和wmin是最大和最小惯性权重,分别取值为 1.2 和 0.4。
优化程序得到的最优参数为:KTP=0.6217,KTI=0.3880,KEP=1.7981,KEI=0.1473。对应的最优适应度函数值为10.2650。适应度函数的寻优历程如图2所示。
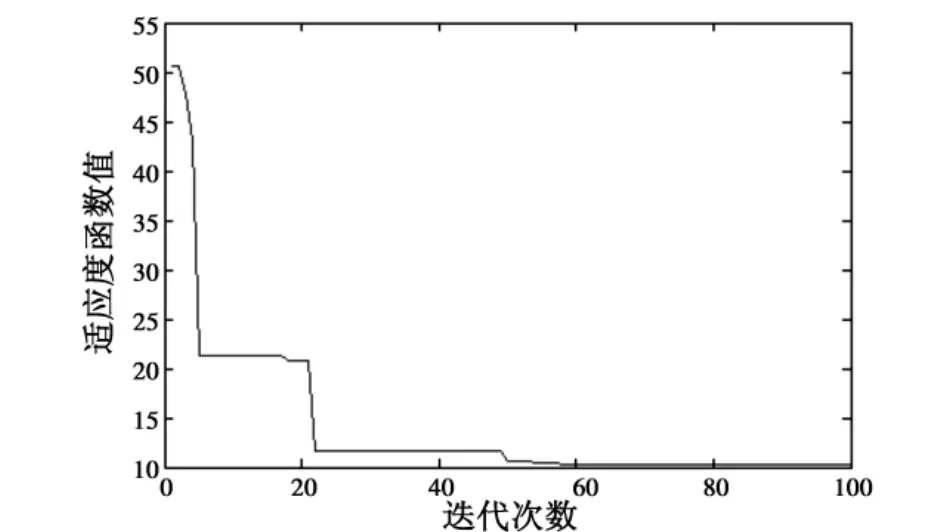
图2 适应度函数值Fig.2 Value of fitness function
3.5 航迹角传递函数的频域分析
首先,利用Matlab的函数Linmod可以得到航迹角传递函数及其Bode图(见图3)。可见,幅频曲线在高频段迅速下降,表示该系统对于高频噪声具有良好的抑制效果。然后,调用Matlab的函数bandwith求出航迹角传递函数的带宽为ωb=1.4 rad/s,满足了文献[10]所要求的舰载飞机着舰飞行控制系统航迹角的响应带宽应该至少为1.2 rad/s的设计要求。
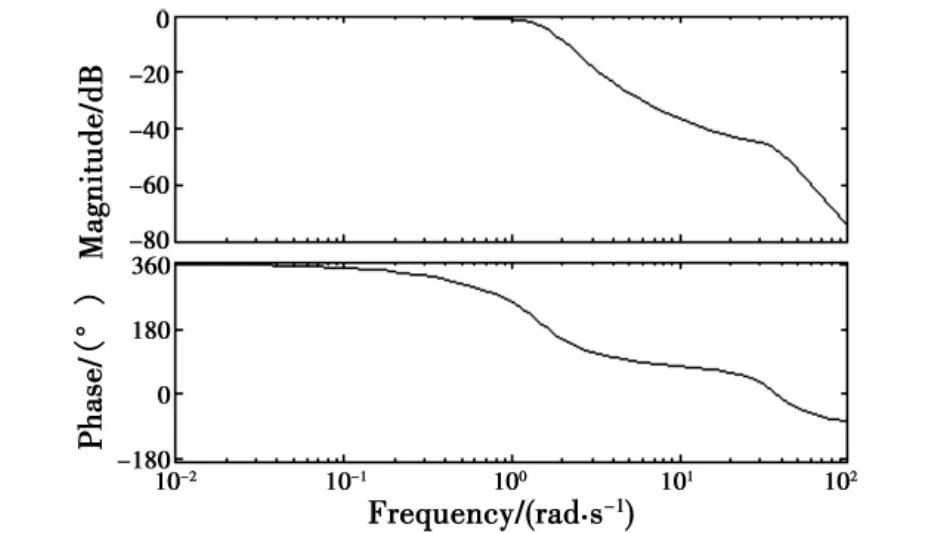
图3 航迹角传递函数的Bode图Fig.3 Bode diagram of flight path angle transfer function
4 仿真结果
以航迹角对阶跃输入信号的响应验证系统的跟踪性能。在仿真进行到1 s的时候施加阶跃指令,系统的响应如图4所示,控制器的输出信号如图5所示。

图4 航迹角的阶跃响应Fig.4 Step response of flight path angle
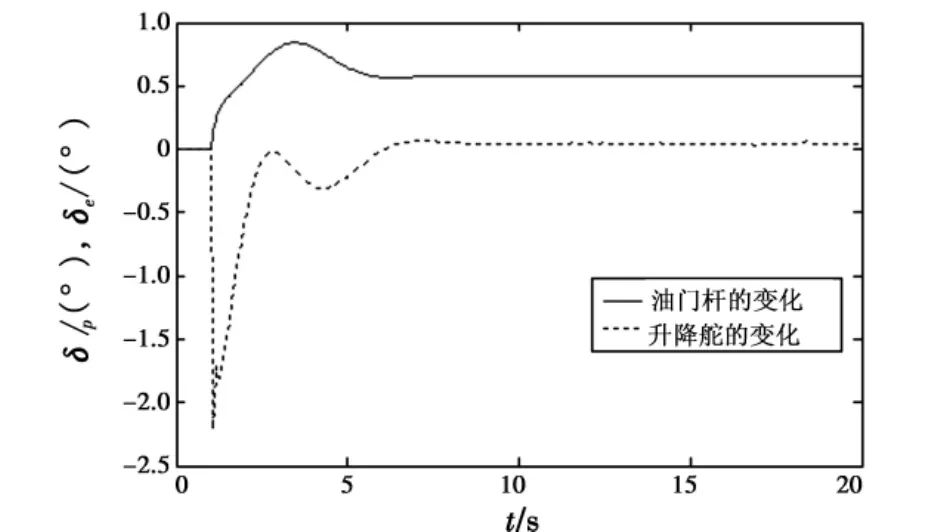
图5 控制器的输出Fig.5 Outputs of the controller
可见,航迹角的响应比较迅速,从阶跃信号开始到峰值时间的间隔为3.80 s,超调量为2.8%。速度所受扰动的最大值为0.039 m/s,可以认为实现了保持速度恒定的目标。图5说明控制器输出的信号使升降舵迅速上偏(下偏为正);同时,增大油门开度以增加发动机推力。这种操作符合人工拉杆推油门的操纵习惯。
5 结束语
为提高舰载飞机着舰时的航迹控制能力,本文将粒子群优化方法和总能量控制系统设计方法结合起来,应用于着舰飞行/推力综合控制系统设计中。频域分析表明该控制系统具有较大的带宽和较小的谐振峰值;时域仿真结果表明所设计的飞控系统的有效性和实用性。
[1]王新华,杨一栋,朱华.低动压着舰状态下飞机的操纵特性研究[J].飞行力学,2007,25(4):29-32.
[2]SUBRAHMANYAM M B.H∞design of F/A-18 automatic carrier landing system[J].Journal of Guidance,Control and Dynamics,1994,17(1):187-191.
[3]LAMBREGTS A A.Vertical flight path and speed control autopilot design using total energy principles[R].AIAA-83-2239,1983.
[4]李爱军,谢燕武,王伟.总能量控制原理在地形跟随飞行控制中的应用[J].飞行力学,2007,25(1):67-70.
[5]刘燕斌,陆宇平,何真.高超音速飞机总能量控制系统的设计和应用[J].应用基础与工程科学学报,2008,16(1):128-135.
[6]汪定伟,王俊伟,王洪峰,等.智能优化方法[M].北京:高等教育出版社,2007:218-222.
[7]章魁,曲立国,黄友锐.一种改进的PSO算法在PID参数优化中的应用[J].电光与控制,2008,15(2):58-61.
[8]邹刚,孙即祥,敖永红.粒子群优化的聚类方法在图像分割中的应用[J].电光与控制,2009,16(2):5-6.
[9]GJB 185-86.有人驾驶飞机(固定翼)飞行品质[S].北京:国防科工委军标出版发行部,1986.
[10]UMRNES J M,HESS R K.Development of the F/A-18A automatic carrier landing system[J].Journal of Guidance,1985,8(3):289-295.
