基于三点支撑的质心测量系统及误差分析
2010-06-04赵章风
钟 江 赵章风 乔 欣 张 宪
浙江工业大学特种装备制造与先进加工技术教育部重点实验室,杭州,310014
0 引言
在机械工程领域,质心测量是一个应用十分广泛的测量项目,如通用汽车的动力总成、汽车总装质心高度的测量,装甲车辆和车体上武器系统的质心分布,火箭、飞机等各类飞行器的质心测量等,都属于质心测量的范畴。质心是车辆性能检测中必测的参数之一,质心位置直接影响车辆的操纵稳定性和行驶安全性。我国国家标准明确规定机动车在空载、静态状态下,向左侧或右侧倾斜的最大侧倾稳定角不允许小于35°[1]。对于高速运动中的飞行器,当其质心位置超差时,将很难调整其飞行方向和姿态,容易造成飞行器偏离轨道或坠毁[2]。因此,质心测量的意义重大。
通常,由于结构原因和设计、加工、装配误差原因,复杂不规则机械产品的质心位置需要通过试验来确定。
赵新通等[3]采用液压驱动的二自由度运动平台测量车辆的质心坐标。骞永博等[4]利用多支点称重法,针对小型弹丸提出了提高其轴向、径向质心测量精度的改进方法。张立彬[5]在原有拖拉机做复摆运动时周期与质心高度之间关系的理论模型基础上,提出了实用测量模型,通过测量摆动周期和改变摆长,计算拖拉机质心高度。Fabbir等[6]和Molari等[7-8]采用平台侧倾试验法测量拖拉机质心高度,将拖拉机放在摆动平台上,依靠平台侧面的钢丝滑轮机构,使平台与拖拉机一起旋转一定角度,测量钢丝绳的拉力,通过静态平衡原理计算出拖拉机的质心高度。
国内外质心测量方法主要存在如下一些问题:①多数测量方法不能一次性测出质心的三维坐标,使用不方便;②缺少完整的分析算法和科学的数据处理方法,无法利用动态测试中获得的实时数据对质心坐标进行科学的高精度预测,导致需要对极限状态进行测试,存在安全隐患。本文基于三点支撑平台反力法,分析质心测量的误差来源和影响程度,可为高精度质心测量装备的设计提供理论依据。
1 测量原理
1.1 测量方法
本文讨论的质心测量平台基于三点支撑可倾斜平台反力原理。传感器测点布置如图1所示(支点1、2、3为传感器安装位置),支点2和支点3位于平台的一端,平台在支点1处沿Z方向做直线升降运动,平台绕支点2和支点3的连线转动。质心测量原理见图2。

图1 质心测量测点分布图

图2 质心测量原理图
设m c和 x c、y c、z c为被测物体的质量和平台坐标系中的质心坐标;mp和xp、yp、zp为支撑平台本身的质量和质心坐标;N1、N 2、N3分别为水平状态下三个传感器的测量值;N′1为支点1在倾斜状态下的测量值;L为支点2与支点3之间的距离;L0为支点1与底端支撑点之间的距离;L d为支点1与支点2和支点3连线的垂直距离;x1、y1、z1为被测物参考坐标系原点O′到平台坐标系原点O的距离;θ为平台侧倾角;θ1为水平平台下表面与支点3(2)和支撑点连线间的夹角;θ2为升降杆1与支点3(2)和支撑点连线之间的夹角;θ3为升降杆1与倾斜平台下表面之间的夹角;S为升降杆1的行程。
利用质心运动定理,并通过坐标变换即可求解出被测物参考坐标系中的质心三维坐标:
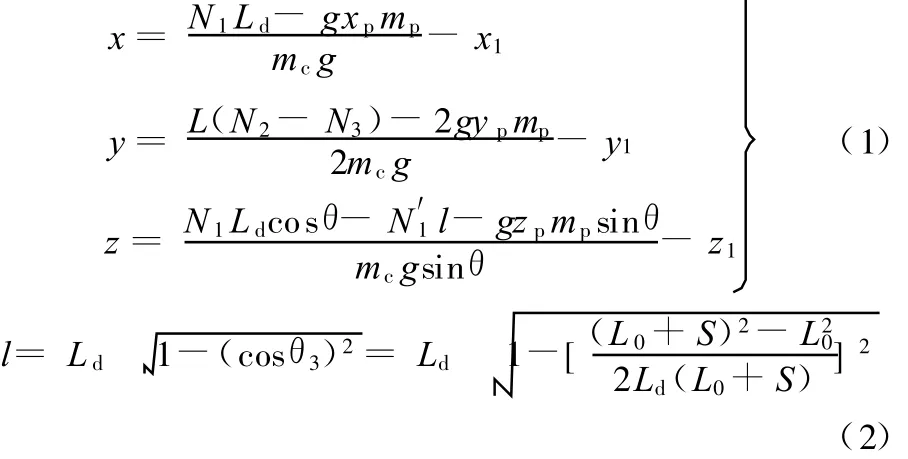
式中,l为 N′1的力臂;g为重力加速度。
1.2 测量机构
质心测量系统主要由平台、球铰副、升降推杆机构、初始位置测量设备和控制系统等组成。平台是被测物体的承载台面,可通过倾斜运动改变测量机构的姿态;球铰副是平台调平和倾斜运动时的回转中心,球铰副部位设置称重传感器;升降推杆机构主要由球铰副、称重传感器、升降机、丝杆、转动销钉等组成,其结构示意图见图3。升降推杆机构为平台升降及工作过程提供动力;初始位置测量设备用于测量被测物在平台上的准确位置,为计算装备质心坐标提供基准点坐标值;控制系统用于平台运动过程的控制、数据采集与处理等。
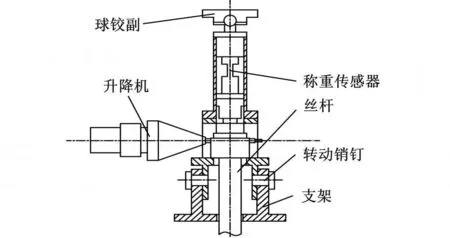
图3 支点1升降推杆机构
2 误差分析
2.1 误差分析方案
质心测量系统中,影响测量精度的因素分为加工安装引起的误差和测量引起的误差。其中加工安装引起的误差包括平台机械加工和安装位置的误差、各球铰或铰链间的位置误差、称重传感器的安装误差、平台的变形、支撑铰链的摩擦力矩等,在加工并装配完成后,这些误差的数值一般不再变化。而测量引起的误差包括各支点作用力的测量误差、支点之间距离的测量误差、平台上表面到三个球铰中心的距离误差、平台调平所引起的误差及开环控制中由于步进电机失步引起的升降推杆的位移误差、被测对象相对平台的初始位置的测量误差等。
平台因加工安装引起的误差属于系统误差,可通过提高机械加工和安装工艺水平以及通过标准体修正补偿的方法进行减小和补偿。而因测量引起的误差属于随机误差,只能通过提高测量仪器本身测量精度来减小。在本测试平台的随机误差中,被测对象相对于测量平台的初始位置测量误差、支点之间距离的测量误差、平台上表面到三个球铰中心的距离误差和平台的调平测量误差可通过高精度测量装置减小其数值,这些误差在实际测量中可以忽略;而由传感器非重复性产生的随机误差及开环控制中步进电机失步引起的升降推杆位移误差是不能补偿的。
由于传感器精度的限制,故角位移的测量精度低于直线位移测量精度。本文在分析过程中,利用平台侧倾角度与升降推杆位移之间的关系,通过精确控制升降推杆的位移来控制平台的侧倾角。升降推杆由步进电机驱动,步进电机由于失步会影响测量结果的精度,但步进电机失步引起的升降推杆位移误差可以利用细分的方法减小。
基于上述分析可知,系统的测量误差主要由测力传感器的测量误差和升降推杆的位移误差决定。因此,质心测量的随机误差合成公式如下:质心水平方向测量误差

质心高度方向测量误差

式中,Kx1、Kx2、Kx3、Ky1、Ky2、Ky3、Kz1、Kz2、Kz3为压 力传感器随机误差引起的误差传递系数;KN′1为支点1处压力传感器随机误差引起的误差传递系数的变化率;KS为升降推杆直线运动产生的随机误差引起的误差传递系数;σN1、σN2、σN3分别为三个压力传感器的随机误差;σS为升降推杆直线运动的随机误差;σx、σy、σz分别为由于传感器的随机误差引起的测量方差。
2.2 平台结构参数对误差影响分析
由质心误差函数及误差传递系数可知,X、Y、Z方向质心位置的误差与传感器测量误差、结构尺寸L d、L及升降推杆1的行程S有关,其中X坐标误差与Ld有关,Y坐标误差与L有关,Z坐标误差与L d、L0和升降推杆1的行程S有关。通过计算可得质心测量误差与 L d、L、L0的关系如图4所示。
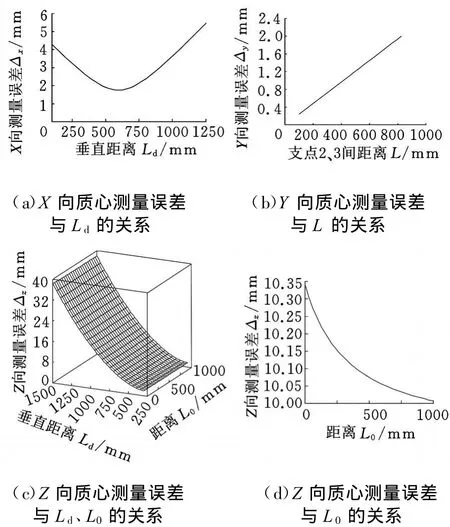
图4 质心坐标误差与结构参数的关系
由图4a可知,Ld=600mm时,X向质心位置的测量误差最小;L d<600mm时,X向质心位置的测量误差随L d的增大而减小;L d>600mm时,X向质心位置的测量误差随Ld的增大而增大。由图4b可知,Y向质心位置的测量误差与L成线性关系,且Y向质心位置的误差随L的增大而增大。由图4c、图4d可知,随着L d的增大,Z向质心位置测量误差也增大,随着L 0的增大,Z向质心位置的测量误差减小,且L d对Z向质心位置测量误差的影响比L0对Z向质心位置测量误差的影响大。
2.3 系统随机误差对测量精度的影响
(1)通过计算可得升降推杆1在平台倾斜过程中的位移误差与Z向质心测量误差的关系如图5所示。
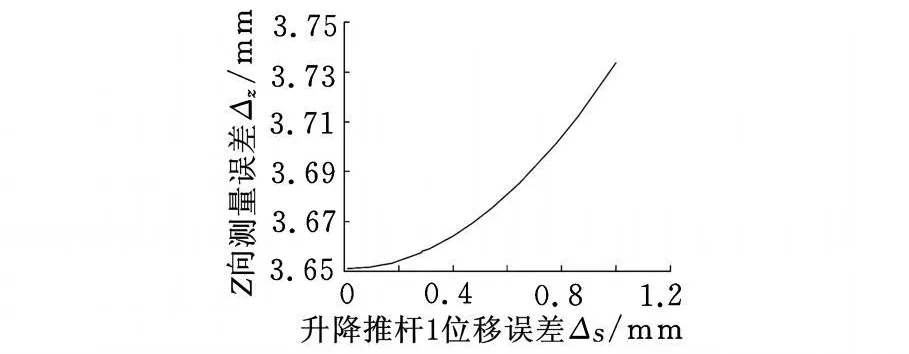
图5 升降推杆1位移误差与Z向测量误差的关系
(2)传感器的测量误差对质量和质心测量都有影响,通过计算可得传感器测量误差对质量、质心测量误差的影响如图6所示。可看出,传感器测量误差与质心、质量测量误差均成线性关系。随着传感器测量误差的增大,质量、质心的测量误差增大。
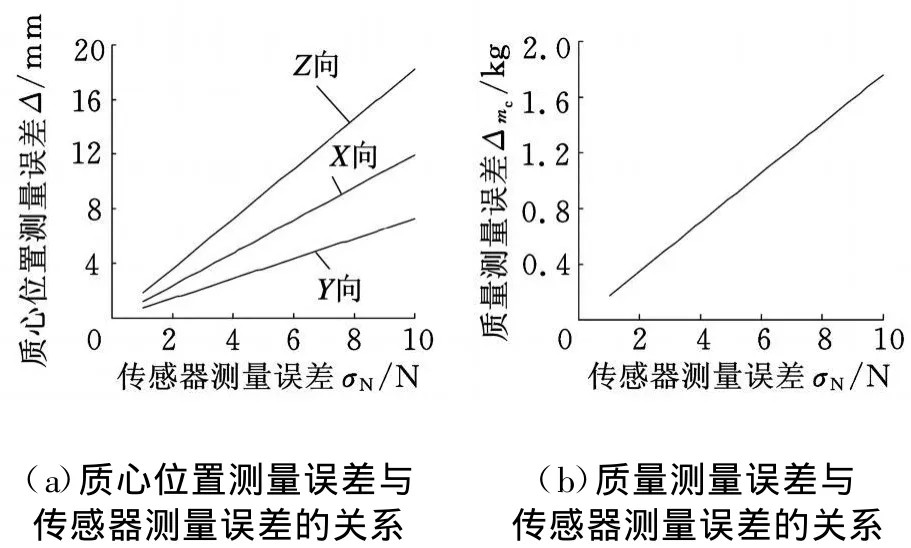
图6 传感器测量误差对质量、质心位置测量误差的影响
对比图6a和图6b可知,传感器测量误差对质心测量误差的影响比对质量测量误差的影响大,在质心测量系统中对测量结果的精度起重要作用。
由图6a三条直线的斜率可知,传感器的测量误差对Z向测量误差的影响最大,对X向测量误差的影响次之,对Y向测量误差的影响最小。
2.4 被测物体质量对测量精度的影响
质心测量误差随被测物体质量的不同也有所差异,质心测量误差随质量变化趋势如图7所示。可以看出,被测物体质量与质心测量误差的关系成指数规律变化。随着物体质量的增大,质心位置测量误差减小,且物体质量对质心Z向测量误差的影响最大,其次是X向测量误差,对Y向测量误差的影响最小。
2.5 Z向质心测量相对误差与升降推杆1位移的关系
Z向质心测量相对误差与支点1的位移之间的关系如图8所示。随着支点1位移S的增大(即支撑平板的侧倾角度增大),Z向质心测量相对误差减小,当S>150mm时相对误差小于7%,且变化趋于稳定。

图7 质心位置测量误差与物体质量的关系

图8 Z向测量相对误差与S的关系
3 试验验证
3.1 试验系统描述
试验被测对象为一正方体金属块,其几何尺寸为60mm ×60mm ×60mm,质量为1.67kg。测量系统主要由计算机、I/O板卡、传感检测装置和由支撑平台、升降推杆机构、底座组成的测试平台组成。
3.2 试验结果及分析
将6次试验各称重传感器的数据列于表1中。由表1数据分析可得:X向和Y向质心实测值的相对误差在5%以内。
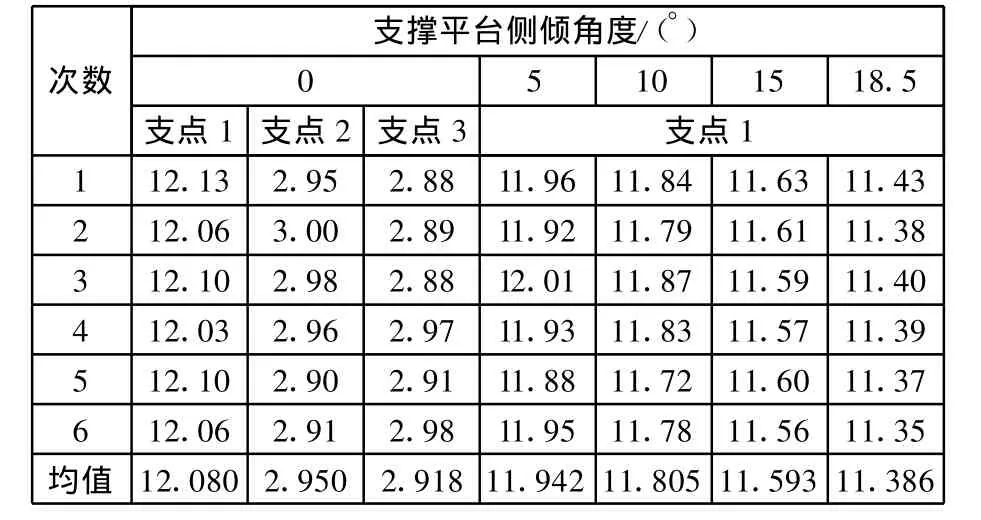
表1 加载标准质量块后各称重传感器的数据 N

图9 Z向质心坐标相对误差随S变化关系
将Z向质心坐标的平均相对误差与支点1处升降杆位移S的实际曲线与理论分析曲线进行对比,如图 9所示。由图9可知,理论分析和试验所得曲线的变化趋势一致,即随着侧倾角度的增大,Z向质心位置测量的相对误差减小,且当升降推杆位移S>150mm(对应支撑平台的侧倾角度为10°)以后,数据趋于稳定。当位移小于150mm时,坐标测试的相对误差随S的变化而急剧变化,说明位移小于150mm时,测试精度较低;而当S>150mm时,理论相对误差和试验得到的相对误差都随升降推杆位移的增大而平缓变化,且理论相对误差均大于试验相对误差。根据误差分析理论,理论误差计算时采用误差的极限值进行计算,而试验过程中的随机误差是以误差极限值为幅值波动的随机值,所以试验结果的最大误差小于理论计算误差。这说明,当位移大于150mm时,所测数据的精度开始逐渐逼近系统测试精度的极限,同时位移越大(即支撑平台的侧倾角越大),测量的精度越高。
4 结语
基于三点支撑方式的可倾斜平台测量系统研究了质心测量方法,分析了各结构参数对测量误差的影响。考虑到测量的安全性,在测量过程中,侧倾角不宜过大,而在支点1处升降推杆升降位移大于150mm时,相对误差随位移变化趋于稳定,使得减少测试次数的同时,仍可保证较高的测量精度和安全性。实际操作中可作如下处理:在升降推杆的位移大于150mm的阶段,对平台上升过程和下降过程进行高频率的数据采样,获得大量的测量数据(升降推杆位移大于150mm时的数据);根据误差分析理论所得出的理论相对误差随支点1处升降推杆位移的变化趋势,采用灰色BP神经网络等方法对测量数据进行建模预测,可以获得较高的测量精度。
[1] 中华人民共和国交通管理标准化技术委员会.GB7258-2004机动车运行安全技术条件[S].北京:中国标准出版社,2004.
[2] 杜明芳,张之江,陆利坤.飞行物体质心的测定[J].计量技术,2002(9):31-32.
[3] 赵新通,赵强.车辆质心测量系统受力分析[J].机械工程师,2004(5):33-34.
[4] 骞永博,吴斌.弹丸质量质心测量方法研究[J].弹箭与制导学报,2006,26(3):126-128.
[5] 张立彬.拖拉机重心高度测定方法和装置的研究[J].浙江农业大学学报,1992,18(4):1-4.
[6] Fabbri A,Molari G.Static Measurement of the Centre of Gravity Height on Narrow-track Agricultural Tractors[J].Biosystems Engineering,2004,87(3):299-304.
[7] Molari G,Rondelli V.On the Definition of Narrowtrack Wheeled Agricultural Tractors[J].Biosystems Engineering,2004,88(1):75-80.
[8] Molari G,Fabbri A.Error Propagation in Agricultural Tractors Centre of Gravity Height Determination[J].Rivista di Ingegneria Agraria,1999,4:224-229.
