基于高阶循环平稳的柴油发动机活塞销振动信号分析

夏 天 王新晴 肖云魁 梁 升

1.解放军理工大学,南京,210007 2.解放军军事交通学院,天津,300161

0 引言

活塞销磨损故障是柴油发动机常见的机械故障之一,主要表现为异响或振动异常,严重时还可能引起拉缸乃至发动机停机,因此必须作为发动机状态监测的重点[1]。活塞销振动是指活塞销冲击活塞座孔或连杆小头座孔而产生的振动,当活塞销和座孔之间的配合间隙由于磨损而逐渐增大时,往往会产生异响或异常振动,配合间隙越大,活塞销产生的冲击力越大,异响或异常振动会越明显。活塞销的冲击不能被直接测量,而是通过活塞、活塞环传向缸体。利用加速度传感器拾取的发动机缸体振动信号包含了与活塞销技术状况相对应的信息,但是缸体振动信号是由内部构件旋转性运动和往复性运动传递到缸体的合成,有用的信息常常淹没在强大的背景噪声中,不利于特征的提取。

工程上存在一类统计特征函数随时间呈现周期性的非平稳信号,这类信号被称为循环平稳信号。高阶循环平稳理论构筑在循环平稳信号的高阶循环统计量的基础上,吸取了高阶统计量和循环平稳两者的优点,理论上可以完全抑制任何高斯和非高斯噪声以及非平稳的高斯噪声的干扰[2],因此是一种理想的信号特征表示方法。目前研究较多的是循环平稳信号的一阶(均值)、二阶(相关函数)循环统计特性,而高阶循环统计量的研究还很少,仅在通信[3]、旋转机械[4-5]等领域有所应用,在内燃机振动方面的应用则鲜有报道。

柴油机稳速时振动信号常常表现为统计特性的周期性,可以证明是典型的循环平稳信号[6],而在加速过程中,振幅逐渐增大,各缸做功间隙时间变短,但是发动机内部各配合副的固有振动频率不会改变,较短的时间间隔内仍可认为是循环平稳信号。目前活塞销故障诊断的研究方法主要有虚拟样机仿真[7]、轴心轨迹计算[8]、时频分析[9]、双谱分析[10]等方法,尚未见到利用高阶循环平稳(higher order cyclostationary,HOCS)理论分析活塞销振动信号的研究报道。本文尝试利用高阶循环累积量谱理论处理活塞销加速振动信号,分析了三种不同的活塞销磨损间隙下的振动信号的循环双谱,讨论了发动机转速对振动信号循环双谱的影响,有效地提取出了能够反映活塞销故障状况的特征值。

1 信号的高阶循环平稳及循环双谱

1.1 高阶循环平稳

高阶循环平稳理论是以循环平稳信号的高阶统计量为理论基础的,包括高阶循环矩、高阶循环累积量以及对应的高阶循环矩谱、高阶循环累积量谱。

k阶循环矩定义为循环平稳信号x(t)对时间t的k阶延迟积的正弦抽取运算[8]：

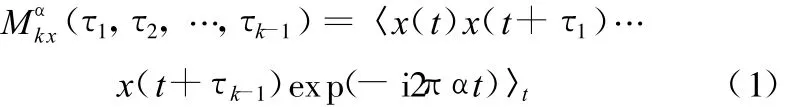
式中,α为循环频率;〈◦〉t表示时间平均;τ1,τ2,…,τk-1为时间延迟。

循环平稳信号 x(t)的循环累积量可以通过信号的低阶循环矩求得：

1.2 三阶循环累积量及循环双谱

三阶循环平稳是高阶循环平稳的最低阶形式,计算量最小,但继承了高阶循环平稳的优良特性。任何平稳的高斯和非高斯噪声以及非平稳的高斯噪声,其高阶循环累积量恒等于零,而高阶循环矩却没有这样的性质,因此从实用的角度考虑,高阶循环统计量最常用的是三阶循环累积量、三阶循环累积量谱即循环双谱。

由式(2),信号的三阶循环累积量可以通过信号的一阶、二阶、三阶循环矩求得：

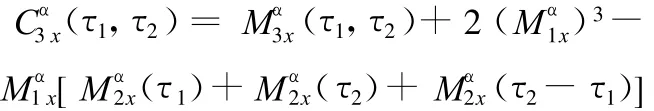
循环双谱是三阶循环平稳的主要应用,定义为

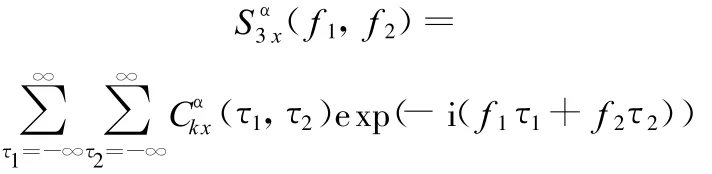
由定义可知,循环双谱是含循环频率α、频率f1、f2三个参变量的多维函数,只能表示一个循环频率下的信号特征。当信号的循环频率为已知时,该表示方法是有效的,但信号的循环频率未知或者循环频率个数较多时,就不能有效地检测出信号的特征[5],柴油机振动信号就存在这样的问题。针对上述问题,本文提出了在特定的循环频率段内,以定步长搜索,计算每一循环频率的循环双谱,并将这些循环双谱累加,以此来表征信号在该频段内多个循环频率中的特征。具体实现步骤如下：

(1)选择特定的循环频率集{α},以定步长Δα搜索,分别计算每一循环频率αj∈{α}的三阶循环累积量

(2)将循环频率集{α}内的每一循环频率αj的三阶循环累积量(τ1,τ2)进行累加 ,得到

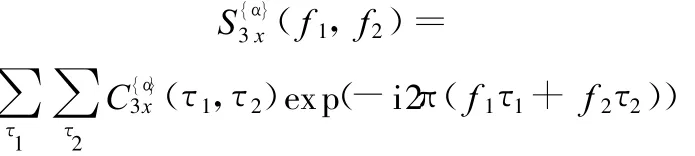
2 数值仿真实验

发动机振动信号含有多个调制源,而相应部件的故障信号往往隐含在调制信号中。但是当调制信号较弱而被其他信号淹没时,传统的解调方法难以奏效。而循环双谱不仅对噪声免疫,且能够识别微弱的调制信号。设调制信号为

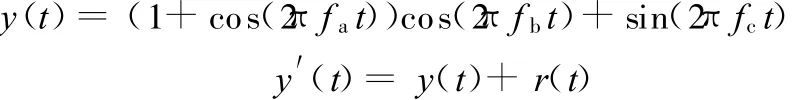
其中,调制频率 fa=30Hz;载波频率 fb=100Hz;频率 f c=20Hz;r(t)为均值为0、方差为1的白噪声;y′(t)为调制信号y(t)受噪声污染后的信号。采样频率 f s=600Hz,采样点数 N=1024。仿真信号y(t)及y′(t)的循环双谱图见图1。

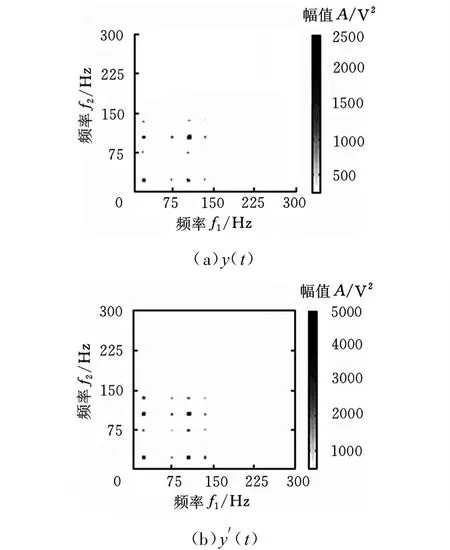
图1 仿真信号 y(t)及 y′(t)的循环双谱取模等高线图

由图1a可以清晰地观察到,在(100Hz,100Hz)、(20Hz,20Hz)处存在谱峰,还可以在双频率平面中得到(100±30)Hz的频率成分,且这些频率成分之间存在着频率的相互作用。对比图1b和图1a,可以获得同样的频率成分,这说明循环双谱不仅能够清晰地反映信号的特征,而且具有较强的抑制噪声的能力。

与双谱不同,在循环双谱中不存在频率耦合现象,只存在频率的相互作用。如上述算例的特征频率为20Hz和100Hz,则在循环双谱图中(20Hz,20Hz)、(20Hz,100Hz)、(100Hz,20Hz)以 及(100Hz,100Hz)处有明显的峰值。正因为循环双谱中特征频率存在直接的相互作用,因而使得循环双谱图能够比较直观地表示信号的特征频率。

3 基于循环双谱的发动机活塞销加速振动信号分析

3.1 活塞销加速振动信号的采集

试验对象为东风EQ6BT型六缸四冲程柴油发动机。试验时将第三缸活塞销与座孔的配合间隙g设置为0.01mm、0.10mm、0.20mm,分别模拟活塞销正常、中度磨损以及严重磨损三种工况。将振动加速度传感器放置在第三缸缸体右侧与油底壳结合处,根据先验知识,该位置测取的振动信号对活塞销磨损故障较为敏感,可以认为是最佳测试位置[1]。

发动机处于加速状态时,内部运动件会产生更强烈的激励,使故障暴露得更明显,这是汽车维修专家所形成的共识。因此本文采用定转速触发采样方式采集加速振动信号,即发动机在加速过程中,如果达到预先设好的触发转速时,采集器开始工作。试验时采集器触发转速设为1800r/min,对应发动机中速状态。采集器采样频率设为25 600Hz,采样点数为16 384。试验过程中,忽略负载的影响,发动机处于空载状态,实际故障检测时将实车上的离合器置于分离状态。

3.2 基于循环双谱的发动机活塞销加速振动信号分析

计算采集到的发动机振动信号的循环双谱。当发动机转速为1800r/min时,发动机曲轴旋转频率 f 0=30Hz,在较短的时间内发动机的速度波动可以忽略不计,故以 f0为频率间隔,重点考察循环频率集{α|α=kf 0,k=1,2,3,…}内振动信号的循环双谱的特征,即计算所有循环频率集内以曲轴旋转频率 f 0及其倍频为循环频率的循环双谱值并累加。三种状况下时域波形如图2所示,其对应的的循环双谱图见图3。

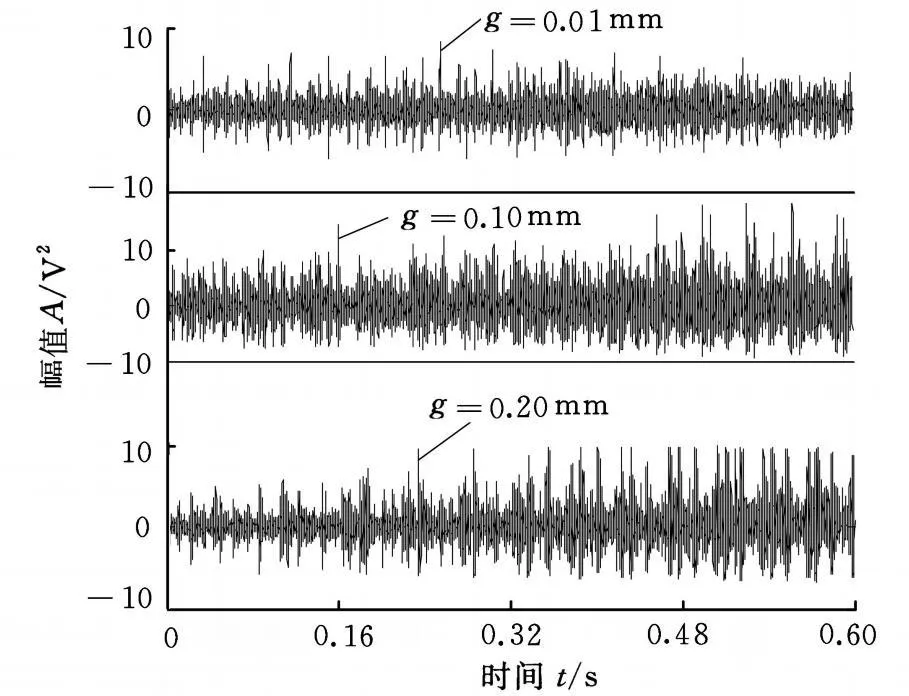
图2 三种活塞销磨损状况下的振动信号时域波形图

由图2可知,随着活塞销与座孔的配合间隙g的增大,发动机振幅A也在增大,但不易于提取相关信息。在图3中,当活塞销正常时,发动机振动信号的循环双谱图频率成分比较少,随着磨损状况的加重,配合间隙增大,循环双谱图中频率成分能量随配合间隙的增大而增加,但是峰值较多,因此需要在整个双频率区间进行搜索,找到与活塞销磨损状况相对应的故障特征值。

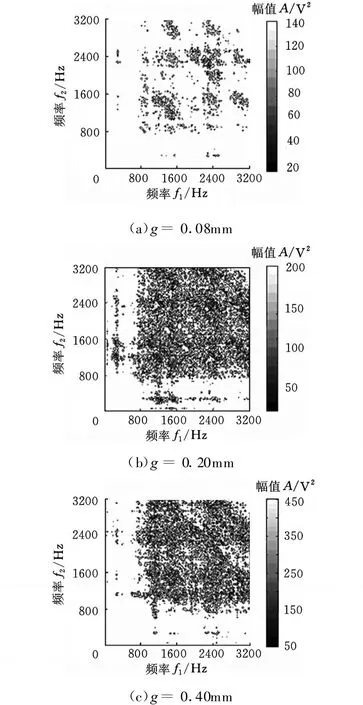
图3 三种活塞销磨损状况下振动信号的循环双谱取模等高线图

从循环双谱图可以看出,大量的频率成分遍布在整个双频率区间,因此采用常用的对角线切片搜索方法可能会丢失对角线以外的重要信息,且循环双谱图中频率峰值太多,故典型峰值搜索法也不便使用。本文提出一种全局搜索策略：在循环双谱图中沿 f 2方向的频带宽度固定取为100Hz,即 该方 向上 频带 区间 为[f′2-50,f′2+50](Hz),沿 f1方向进行搜索,当搜索到频带区间为[f 1a,f 1b]时,可以得到一个矩形平面,其左下角的坐标为(f1a,f′2-50)(Hz),右上角坐标为(f 1b,+50)(Hz)。将该平面内循环双谱值进行累加,如果该平面内的平均累加值能够反映活塞销磨损故障的变化规律,则认为该平面是循环双谱特征频率平面。每次采样时,由于发动机转速的波动性,特征频率峰值会发生偏移,故提取特征频率平面比提取特征频率峰值更具有一般性和稳定性。

按照上述全局搜索策略,搜索图3所示的活塞销三种磨损间隙下的振动信号的循环双谱图的特征频率平面。为了防止遗漏,将 f 2方向上相邻的频带设置为50%的重叠,搜索得到的前5个最明显的特征频率平面如图4所示,其对应的平面内循环双谱幅值的平均累加值变化规律如表1所示。可以看出,搜索得到的前5个特征频率平面内的循环双谱幅值的平均累加值随活塞销磨损间隙的增大而显著增大,能够反映活塞销配合间隙的变化规律,因此可以作为诊断活塞销磨损间隙的特征量。

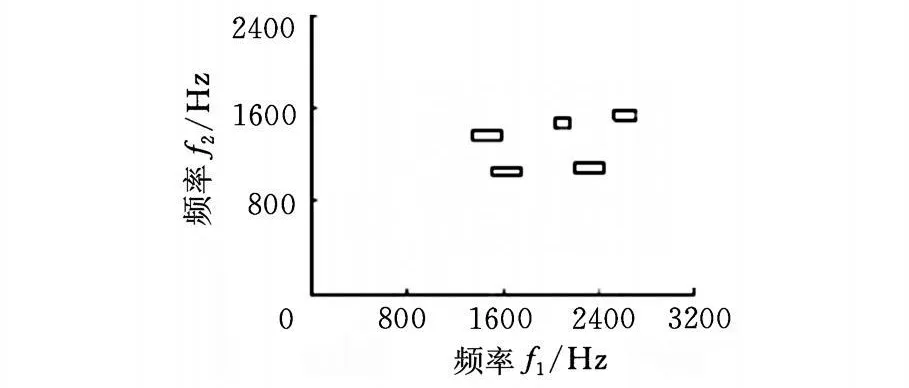
图4 搜索得到的前5个特征频率平面

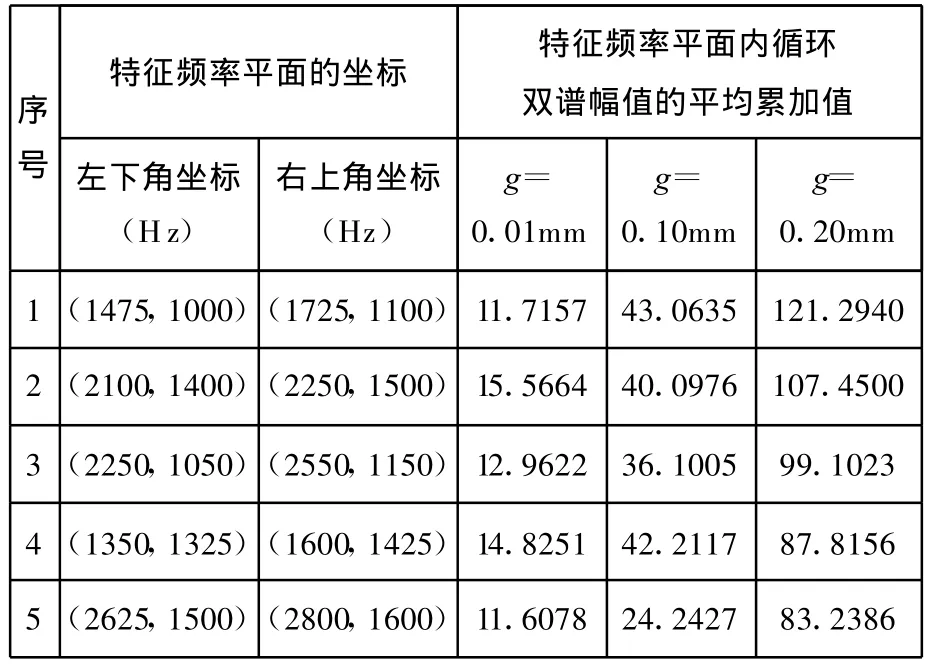
表1 前5个特征频率平面内循环双谱幅值的累加值

4 结论

(1)当信号的循环频率未知或循环频率太多时,可在特定的循环频率频段内以定步长进行搜索,计算所有循环频率的循环双谱并累加,以此估计信号的循环双谱。

(2)柴油发动机活塞销振动信号具有高阶平稳性,利用高阶循环平稳理论分析振动信号,能够消除噪声的影响,可以提取出隐含在振动信号中且能够反映柴油发动机活塞销磨损状况的信息。

(3)活塞销振动信号的循环双谱图中频率成分分布在整个频率区间内,利用全局搜索策略,获得5个特征频率平面,该特征频率平面内的循环双谱幅值的平均累加值随活塞销磨损增大而明显增大,可以将其作为对活塞销磨损故障进行诊断的特征值。

(4)与双谱等高阶累积量谱相比,高阶循环累积量谱计算量巨大,不适合于故障诊断的在线应用,因此必须寻找高阶循环累积量谱的简化算法或快速算法,以弥补目前算法的不足,使之适合工程在线应用。

[1] 肖云魁.汽车故障诊断学[M].北京：北京理工大学出版社,2006.

[2] Spooner C M.Theory and Application of Higherorder Cyclostationarity[D].Berkeley：University of California,1992.

[3] 冯祥,李建东.基于高阶循环累积量的SQAM信号调制识别算法[J].电子与信息学报,2007,29(1)：125-128.

[4] Zhu Z K,Feng Z H,Kong F R.Cyclostationarity Analysis for Gearbox Condition Monitoring：Approaches and Effectiveness[J].Mechanical System and Signal Processing,2005,19(2)：467-482.

[5] 朱忠奎,孔凡让,王建平,等.循环双谱及其在齿轮箱故障识别中的应用研究[J].振动工程学报,2004,17(2)：224-227.

[6] Antoni J,Daniere J,Guillet F.Effective Vibration Analysis of IC Engines Using Cyclostationarity.Part I：a Methodology for Condition Monitoring[J].Journal of Sound and Vibration,2002,257(5)：815-837.

[7] 白欣,黄博,王立臣.基于虚拟样机的发动机活塞销故障诊断研究[J].汽车技术,2005(4)：20-23.

[8] 丁恒鉴,肖云魁,阳建成,等.汽油机活塞销轴心轨迹计算及在故障诊断中的应用[J].内燃机学报,2001,19(2)：187-191.

[9] 郑海波,李志远,陈心昭,等.基于时频分布的发动机异响特征分析及故障诊断研究[J].内燃机学报,2002,20(3)：267-272.

[10] 肖云魁,李会梁,王保民,等.基于双谱的柴油发动机活塞销故障诊断[J].内燃机学报,2008,26(4)：369-373.