引线成形中劈刀与引线拐点运动学关系研究
2010-06-04周洪军
周洪军 韩 雷
中南大学现代复杂装备设计与极端制造教育部重点实验室,长沙,410083
0 引言
随着IC封装向系统级集成和向小型化、轻薄化方向发展,引线互连封装对线弧轮廓形状的要求越来越高,尤其在多芯片叠层互连中,低层芯片的线弧高度必须降低,以避免不同层引线交叉短路,高层芯片的线弧同样必须保持一定高度以避免引线暴露在外面。而在引线成形过程中,劈刀的运动对引线轮廓的形状起决定作用,所以在引线成形中,研究劈刀与引线的相互运动关系有重要意义。
劈刀运动对引线成形的影响已经引起了许多学者的关注。文献[1]用有限元仿真的方法,研究了各个劈刀运动轨迹参数对引线轮廓形状及内部张力的影响状况;文献[2]用一种统计的方法——曲面响应法分析了引线轮廓各参数的主要影响因素和相互关系;文献[3]用有限元的方法仿真了引线成形的过程;文献[4]提出了一种弹簧模型分析引线成形方法。在以往对引线成形的研究中,大都采用仿真的方法,很少有通过实验来分析劈刀运动对引线成形的具体影响过程。
由于引线线形的形成与引线拐点(引线上局部塑性区)有很大关系,因此,为研究劈刀运动对引线成形过程的影响规律,本文在以引线键合视频录像分解的图像序列基础上,重点分析了劈刀与引线拐点间的运动关系,力求对引线成形过程有更进一步的认识。
1 图像获取
引线键合的图像获取过程为:首先利用机器视觉获得引线键合的视频录像,然后再将视频录像分解为序列图像。本文采用Kulicke&Soffa公司自动键合机拍摄的视频,其中劈刀直径约为1.6mm,金线直径约为25.4μm,视频分解的时间间隔为每帧视频分解一幅图像,将视频全部分解得到413幅图像。按照分解得到的图像顺序,将序列图像编号为1,2,…,413,整个键合时间实际约为50~100ms,所以每帧图像时间间隔约为0.12~0.24ms。以下计算位移以像素为单位,时间以帧为单位,不考虑实际标定。其中对引线成形过程的描述大约从第70幅到第350幅,约为280幅。每幅图像大小为 320pixel×240pixel。图1所示为分解得到的第181幅、第276幅图像。

图1 分解得到的图像
2 劈刀运动轨迹计算
2.1 相位相关法
相位相关法最早于20世纪70年代被提出来,是一种非线性、基于傅氏功率谱的频域相关技术,经常被用来检测两幅图像之间的平移,也可以用于检测两幅图像之间的旋转与伸缩。相位相关法对噪声不敏感,且不受帧间光照变化的影响,是一种强鲁棒性的图像匹配方法,因此在用相位相关法求平移量之前不需要将亮度均一化[5]。
假设 f(x,y)表示尺寸为M×N的图像,该函数的二维离散傅里叶变换为

式中,F(u,v)为复变函数;u、v为频域变量,u=0,1,…,M-1;v=0,1,…,N-1;x、y为空间或图像变量。
二维离散傅里叶逆变换为

设劈刀模板图像 I1与图像序列中某一图像I2的重叠位置为(x0,y0),则图像I1、I2的互功率谱为

式中,*为共轭符号;I(ε,η)表示某一位置像素点的灰度值。
对式(3)两边进行傅里叶变换将在(x0,y0)处产生一个δ函数,因此只要检测式(3)傅里叶逆变换结果的峰值位置,即可得出该图像中劈刀的位置。δ函数的峰值在理想情况下应为1,但是由于噪声等原因,其峰值往往小于1,峰值的大小描述了两幅图像匹配程度的好坏。遍历所有序列图像,即可获得劈刀运动轨迹。
2.2 实验结果
利用MATLAB 7.1图像处理工具箱[6]对分解的序列图像采用相位相关法进行键合过程劈刀运动轨迹求解时,首先需要确定参考图像的大小,参考图像选择得太小,计算时间会增长;模板选择太大,对劈刀位置的识别准确度又会降低,使劈刀位移计算不准确。本文通过反复实验选择模板大小为20mm×20mm。图2a为第181幅图像的互功率谱傅里叶逆变换的δ函数值分布图像,循环计算得到的劈刀运动轨迹如图2b所示。
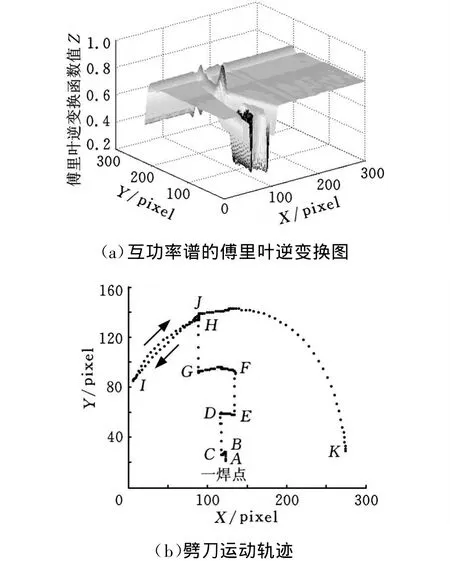
图2 相位相关法计算劈刀运动轨迹
3 引线拐点识别
为了研究引线键合过程中引线拐点的运动情况,必须先对序列图像进行引线拐点的识别。由于拐点的位置必定是引线上曲率极值点,因此对引线拐点的识别即为求引线上的曲率极值点,如图3所示。
目前常用的计算离散曲率的方法有曲率尺度空间的高斯滤波器卷积算法和分段拟合算法等,前一种算法受平滑因子σ影响,σ太大容易丢失曲率值较大的点,太小容易引入噪声点;而后一种算法引入了拟合计算的固有计算误差。本文采用文献[7]中一种点到弦距离累积估计曲率的算法进行引线拐点识别,与前面算法相比,该方法具有较好的鲁棒性。
3.1 点到弦距离累积估计曲率法
设曲线 Γ(i)=(x(i),y(i)),i=1,2,…,n,由n个离散数据点p={p 1,p2,p 3,...p n}组成,如图4所示。

图3 引线拐点示意图
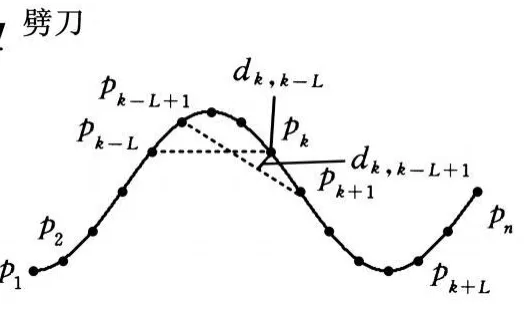
图4 点到弦的距离示意图
为了测量pk点曲率hL(k),向前后各取L个离散数据点,并分析这一段曲线。分析可知,曲线的两个端点为p k-L和p k+L,连接p k-L和p k得到一弦pk-Lpk,计算 pk到这一弦的垂直距离dk,k-L,如图4所示。然后向前移动弦的一个点,弦端点变为p k-L+1和 p k+1,同样计算 pk到弦的垂直距离dk,k-L+1。重复上面计算,直到弦的两端点分别为p k、p k+L,当点p k位于弦左侧时,定义距离为正,反之为负。最后累积所有距离表示pk点估计曲率h L(k):
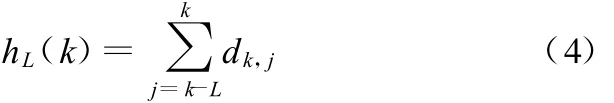
其中,dk,k-L=dk,k=0,式(4)可简化为

对于曲线Γ,按式(5)遍历曲线上的所有点,即可得到曲线上每一点上点到弦的距离累积和SL(pk),用来表征曲线Γ上p k点的曲率。文献[8]证明了点到弦的距离累积曲率和曲线曲率之间具有相似性,且存在常数c,使得

式中,k(pk)表示pk点的曲率。
式(6)表明了点到弦的距离累计曲率可以间接地表征离散曲线曲率的相对大小。
3.2 实验结果
利用点到弦的距离累积估计曲率法测得所有序列图像中引线的曲率分布,将引线曲率分布归一化,设定曲率阈值为0.2,根据曲率极值点及所设的阈值(曲率值大于阈值的极值点为拐点)分别得到了序列图像中四个拐点在X、Y方向的运动轨迹,如图5所示。
从图5a可以看出,拐点1在整个过程中位移改变很小。分别计算四个拐点的标准差如表1所示。
从表1可以清楚地看出,与其他拐点运动相比,拐点1基本不动。在整个键合过程中,可以认为劈刀和引线以拐点1为中心在做旋转和拉伸运动,而且拐点1在第一焊点形成后不久出现,对第一焊点具有一定的保护作用,可防止与芯片发生脱落等。

表1 各拐点位置标准差 pixel

图5 拐点1~拐点4的运动轨迹
3.2.1 劈刀和拐点旋转角分析
由上述分析可知,拐点1位置基本不动,为了得到劈刀与2、3、4三个拐点的旋转运动的关系,定义旋转角为某一时刻劈刀或拐点当前位置点和第一焊点的连线与水平线的夹角(图3)。设劈刀和 2、3、4 拐点的旋转角分别为 θ、θ2 、θ3、θ4,其计算结果如图6所示。
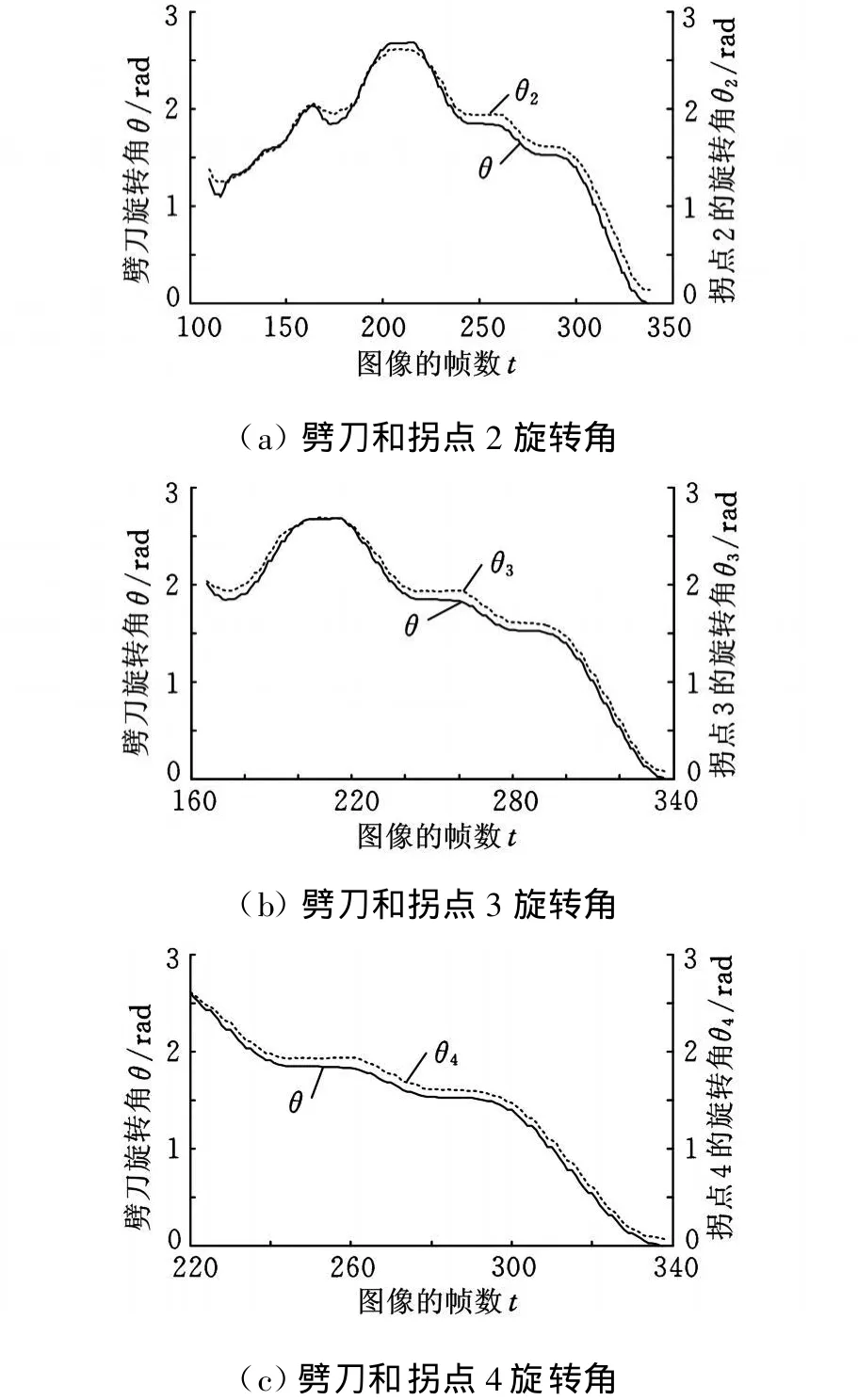
图6 劈刀和拐点旋转角
从图6中可以看出,2、3、4三个拐点与劈刀的旋转角变化分布非常相似,说明引线成形过程中,引线在劈刀的作用下其运动是一种近似于准刚体的运动。而且三个拐点旋转角大小的整体分布都大于劈刀的旋转角,说明在该过程中,引线的运动相对于劈刀有一定的滞后性,引线在出现拐点的这些位置上产生了较大的塑性变形。比较2、3、4三个拐点的旋转角,发现其与劈刀的旋转角接近程度依次增加,对应于拐点与劈刀的距离依次减小。
3.2.2 劈刀和拐点速度分析
上述分析表明了引线运动是一种准刚体运动。为了进一步说明,根据前面得到的劈刀和拐点的轨迹,计算得到各自的像素数分布,如图7~图10所示,其中,纵坐标为每帧图像的像素数。
从图7~图10可以看出,劈刀和拐点以及拐点与拐点之间的运动速度分布也具有很大的相似性,从另一个角度也说明了引线运动可以认为是一种准刚体运动。在MATLAB中利用互相关法分别计算X、Y方向劈刀与拐点之间速度分布曲线的相似程度,以R表示。计算结果如表2所示。由表2可知,劈刀与拐点速度分布的互相关性系数值R都在0.8以上,所以高度相关。而且2、3、4三个拐点与劈刀的相关值R也是依次增加,这与上述旋转角的实验结果是一致的,进一步说明了引线运动是一种近似准刚体的运动。

图8 拐点2速度分布
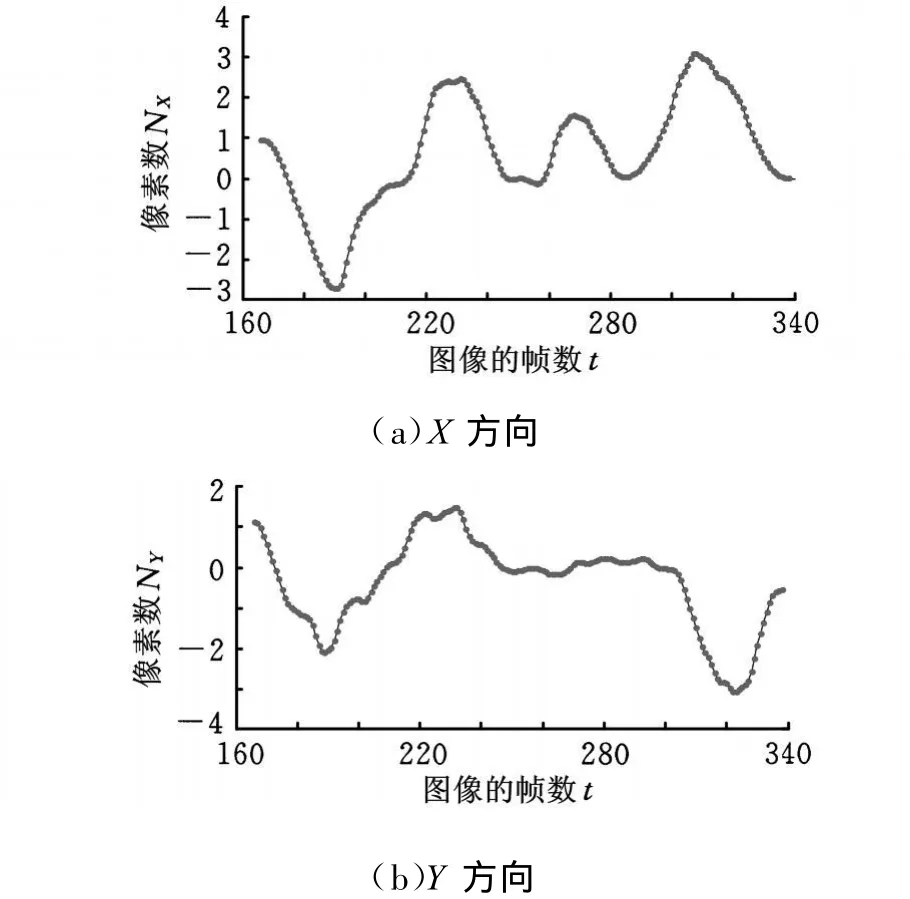
图9 拐点3速度分布
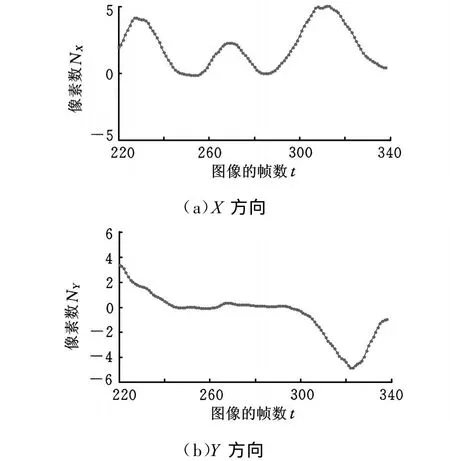
图10 拐点4速度分布

表2 各拐点与劈刀运动速度相关系数R值
3.2.3 下降段拟合圆圆心位置分析
在键合过程中,劈刀的下降段运动是最后一个运动段,对引线的最终形状有重要影响。由于劈刀的下降段运动是圆周运动(图2b中JK段),而且拐点与劈刀的运动具有高度相关性,所以分别采用圆拟合法[9]拟合得到劈刀和2、3、4三个拐点在下降段运动轨迹的圆心位置。
设(xi,yi)、Ri(i=1,2,3,4)分别表示拟合得到的劈刀和2、3、4三个拐点下降段轨迹圆的圆心和半径。根据最小二乘法拟合原理,目标函数F(xi,yi,Ri)的表达式可表示为

采用极值法使目标函数最小,参数 xi、yi、Ri满足:

计算式(9)得到参数(xi,y i)、Ri即为拟合圆的圆心和半径,结果如图11所示。其中由于拐点1在整个过程中位置基本不变,所以以位置平均值作为其圆心位置。
图12所示为键合完成后引线的最终线形。
结合图11和图12可以看出,引线最终形成的M 形线形中,1、2、3、4四个拐点的相对位置与其拟合圆圆心的相对位置有很大相似性,即拟合圆圆心的相对位置构成的形状反映出了引线的最终线形。

图11 劈刀和拐点下降段轨迹圆拟合
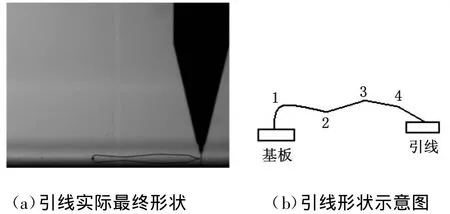
图12 引线最终线形
4 结论
通过引线键合视频分解得到图像序列,利用相位相关法和点到弦距离累积曲率估计法分别计算获得了劈刀和引线拐点的运动轨迹。对获得的运动轨迹,定义和计算了劈刀和拐点的旋转角。比较各自旋转角发现,在劈刀作用下,引线运动可以近似认为是一种准刚体运动。通过计算分析劈刀和拐点的速度分布,发现其速度分布也具有高度相关性,且距离劈刀越近的拐点速度分布与劈刀的相关性也越高,进一步说明了引线运动的准刚体性质。最后对劈刀和拐点的下降段运动轨迹进行圆拟合,得到了各圆心的相对位置分布,发现各圆心的相对位置分布与引线最终的线形存在相似的对应关系。为进一步研究劈刀运动与引线微位移、微应力等动态特性提供了有价值的参考。
[1] 范柱子,陈学东,姜伟.IC引线键合引线轮廓成形仿真研究[J].机械与电子,2005(5):59-62.
[2] Groover R,Shu W K,Lee S S.Wire Bond Loop Profile Development for Fine Pitch-Long Wire Assembly[J].IEEE Transactions on Semiconductor Manufacturing,1994,7(3):393-399.
[3] Liu D S,Chao Y C,Wang C H.Study of Wire Bonding Looping Formation in the Electronic Packaging Process Using the Three-dimensional Finite Element Method[J].Finite Elements in Analysis and Design,2004,40:263-286.
[4] Lo Yulung,Ho Tienlou,Chen Jauliang.Linkage-Spring Model in Analyzing Wire Bonding Loops[J].IEEE Transactions on Components and Packaging Technology,2001,24(3):450-456.
[5] 漆驰,刘强,孙家广.摄像机序列的全景图拼接[J].计算机辅助设计与图形学学报,2001,13(7):605-609.
[6] 王正林,刘明.精通MATLAB7[M].北京:电子工业出版社,2006.
[7] Awrangeb M,Lu G.Robust Image Corner Detection Based on the Chord-to-Point Distance Accumulation Technique[J].IEEE Transactions on Multimedia,2008,10(6):1059-1072.
[8] 彭铁根,吴惕华.基于负曲率极值点的零件识别与检测技术研究[J].系统仿真学报,2006,18(11):3058-3062.
[9] 徐国旺,廖明潮.拟合圆的几种方法[J].武汉工业学院学报,2002(4):104-106.
