立式回转药柜结构优化设计与运动仿真
2010-06-04张志强刘相权
张志强 贠 超 刘相权 刘 扬
1.北京航空航天大学,北京,100083 2.北京信息科技大学,北京,100192
0 引言
目前国内医院药房的药品存储设备主要为固定式货架,药品存储分散,空间利用率低,因而药房工作费时费力,处方处理效率低。随着医疗体制改革和医院改革向着信息化方向发展,迫切需要开发一种适合中国国情的药房自动化设备。
笔者开发的药房自动化设备包括立式回转药柜和快速出药系统两部分。快速出药系统适用于具有规则形状的盒装药品,能够实现药品的密集存储、自动上药、自动出药;立式回转药柜对药品包装适应性强,但受传动链速度的限制,药品出库和入库效率较低,储药量也偏低,是对快速出药系统的补充。
1 立式回转药柜工作原理
如图1所示,立式回转药柜主要由以下部分组成[1-2]:
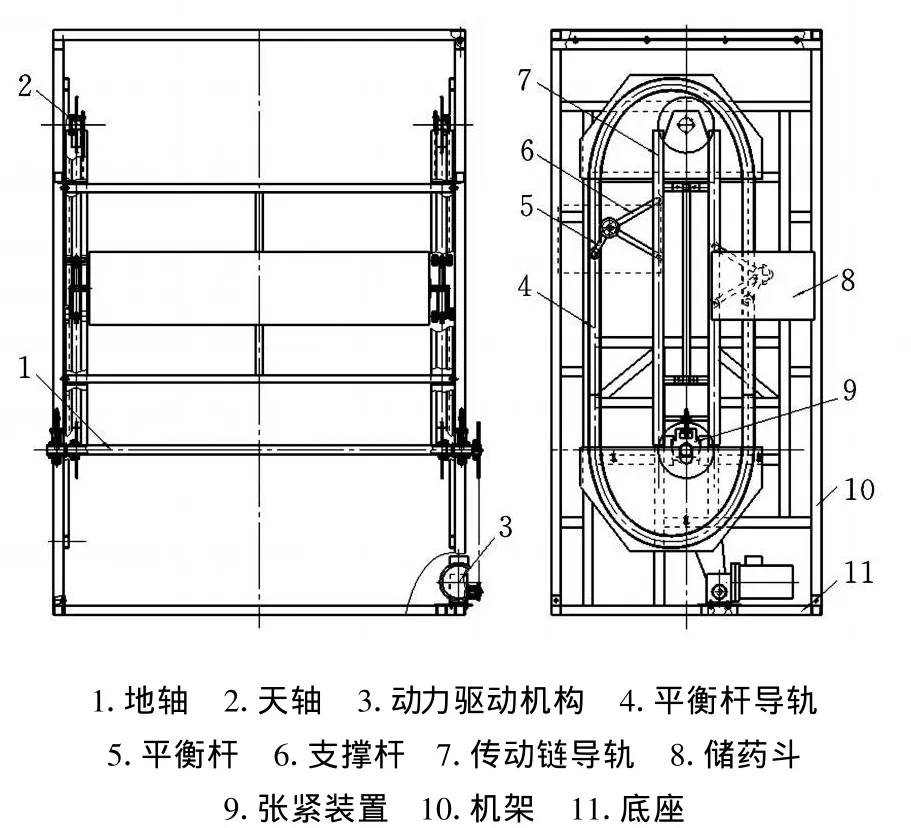
图1 立式回转药柜机械结构图
(1)天轴、地轴为上下传动轴,地轴为主动轴,天轴为被动轴,主要承载药品和储药斗的重量。轴的两端安装有链轮等传动机构,带动储药斗做垂直与回转运动。地轴是一根通轴,一端与传动链轮、电动机的减速箱连接。
(2)动力驱动机构由电动机、减速器、一级链传动、二级链传动组成,其中,一级链传动由一级小链轮、一级链条、一级大链轮组成,二级链传动采用双链轮封闭链条式链传动,由2个同轴的主动链轮、2个同轴的从动链轮及与主从动链轮相啮合的链条组成。
(3)平衡杆及平衡杆导轨主要用于保持储药斗处于水平及平行状态,以保证储药斗在高速运转过程中不出现翻斗现象及药品不从储药斗中掉出。平衡杆导轨通过焊接固定到柜体骨架上。
(4)储药斗及支撑杆。支撑杆的一端通过铰接与链条连接,支撑杆的另一端、平衡杆的一端以及可移动储药斗的一端连接在一起,随着链条的运动做垂直及回转运动。
(5)传动链导轨通过焊接固定到柜体骨架上,主要用于传动链的导向,保证传动链条的平稳运行并降低噪声。
(6)张紧装置主要用于储药斗传动链条的张紧,防止链条在负载运行中的伸长而影响传动。
(7)机架、底座与壳体。机架主要作用为天轴与地轴的支撑,与底座相连。壳体由4根立柱和四周面板组成,包括存取窗口的翻门及操作面板等,起覆盖作用。
(8)电气控制系统包含PLC、电气柜、安全检测装置等,通过总线与计算机联网,用来控制回转药柜运行,保证储药斗快速准确地运转至存取位置。
立式回转药柜运转时,由动力驱动机构的电动机提供动力,通过减速器和一级链传动两级减速后,带动地轴转动,从而驱动2个同轴的主动链轮,2个主动链轮再分别通过链条传动牵引支撑杆和平衡杆而带动所有储药斗做循环运动。药品放置在可移动储药斗中,接收存取指令后,储药斗按最短路径运动,最快送达存取口。基于数据库的药品监控系统安装在工控机中,药品监控系统发出指令驱使立式回转药柜运转即可完成药品的存取操作。
2 相邻储药斗运动不干涉条件分析
图2为二级链传动系统及储药斗示意图。经设计选用节距为12.7mm的08A型链[3],与储药斗相连接的双支撑杆在链条上的跨距为大跨距,双支撑杆与相邻双支撑杆之间跨距为小跨距。储药斗总数量为12个,均匀分布在链条上。
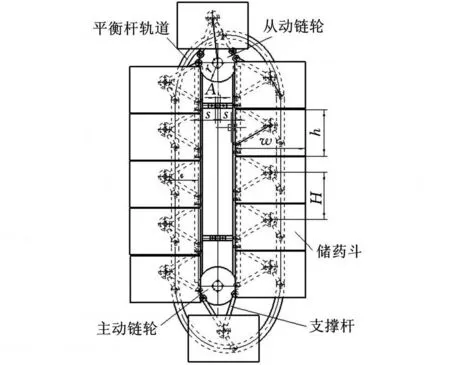
图2 二级链传动结构示意图
主动链轮、从动链轮节圆半径均为r,支撑杆外伸量为c,w、h分别为储药斗外形轮廓的宽和高,垂直运动的两相邻储药斗支轴中心相距 H,连接梁的安装尺寸界限为A,s为储药斗与连接梁之间安全距离。
以从动链轮中心O为原点,建立参考坐标系如图3所示,O1、O2、O3、O4依次是连接储药斗1、储药斗2的支撑杆1、2、3、4与传动链条连接处,坐标分别为(x1,y 1)、(x2,y 2)、(x3,y3)、(x4,y4)。A1为储药斗1与支撑杆1、2的支轴中心,A2为储药斗2与支 撑杆3、4的支轴中心。A1、A2的坐标分别为(X1,Y1)、(X2,Y2),链轮逆时针旋转。
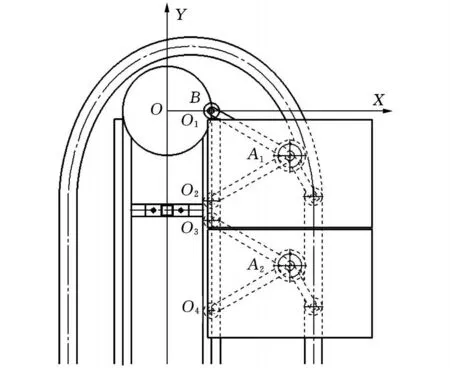
图3 两相邻储药斗运动初始位置
为分析方便,假设B点为从动链轮节圆上的一点,在运动开始时B点与链轮中心O保持水平并与 O1 重合,O1、O2、O3、O4 在同一竖直线上。储药斗运动初期,O1沿半径为r的圆弧逆时针旋转,O2、O3、O4保持竖直向上运动,直至O2到达O点高度后,O1、O2做半径为 r的同一圆弧运动。θ0为O1、O2两点同时沿圆弧旋转时连线OO1和OO2之间的夹角,θ1为B点的旋转角度,θ2为O2、O3两点同时沿圆弧旋转时连线OO2和OO3之间的夹角。
设储药斗1、储药斗2运动中,支轴中心A1和A2在水平方向和竖直方向的距离为ΔX和ΔY,则相邻两储药斗运动不干涉条件为
若0≤ΔX ≤w,则需
若ΔX >w,则相邻储药斗运动无干涉[4]。
如图3所示,储药斗支轴中心 A1、A2以从动链轮中心O做圆弧旋转时,该圆弧并非是一个完整的半圆曲线。下面以从动链轮节圆上B点的旋转角度θ1为变量,进一步分析式(1)在相邻储药斗8个不同运动阶段的情况。
2.1 运动第1阶段
0≤θ1≤θ0时,O1沿半径为r的半圆做圆周运动,储药斗1支轴中心 A1做变直径的圆弧旋转,O2、O3、O4与储药斗2支轴中心 A2做竖直向上运动直至O2与O在同一水平线上。在此运动过程中,O1~O4的坐标(单位:mm)分别为
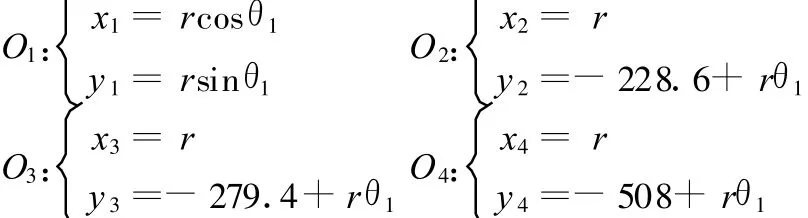
则
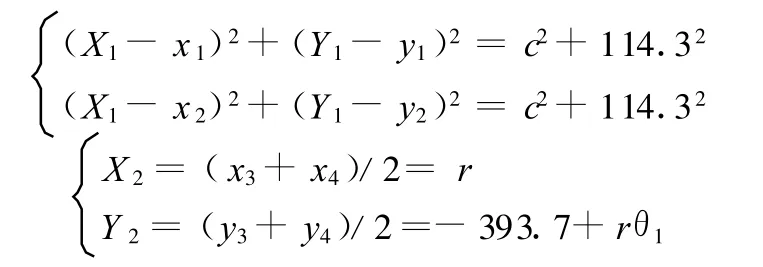
借助MATLAB,可求解出第一阶段 X 1、Y 1的解析式:
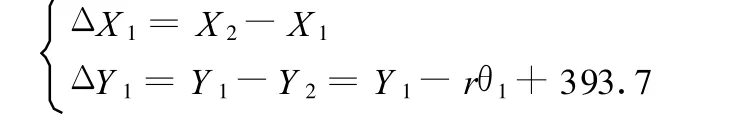
由式(1)得出
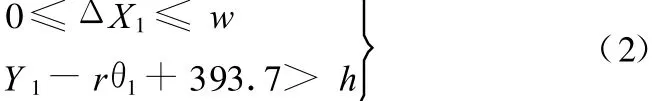
2.2 运动第2阶段
θ0 <θ1 ≤θ0+θ2时,O1、O2同时做半径为r的圆弧运动,储药斗1支轴中心A1做半径为R的圆弧运动,O3、O4与储药斗2支轴中心A2继续做竖直向上运动直至O3与O在同一水平线上。
在此运动过程中,A1、A2的坐标分别为
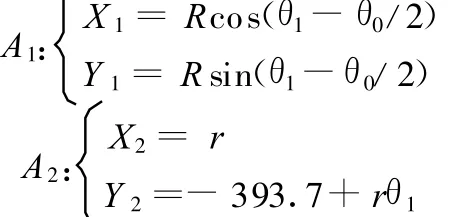
R可由下式求解:
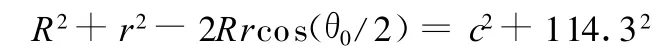
则
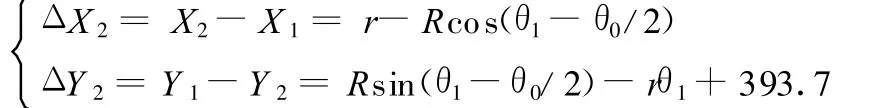
由式(1)得出
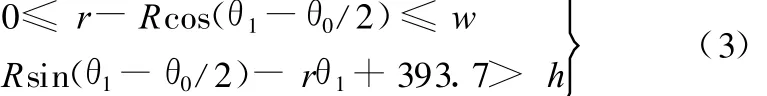
2.3 运动第3阶段
θ0+θ2 <θ1 ≤π时,O1、O2同时做半径为r的圆弧运动,储药斗1支轴中心A1做半径为R的圆弧运动,直至O1与O在同一水平线上。O3做半径为r的圆弧运动,O4继续做竖直向上运动,储药斗2支轴中心A2做变直径的圆弧旋转。在此运动过程中,A1的坐标为
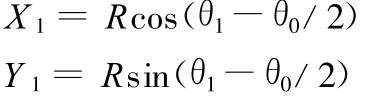
O3、O4的坐标分别为
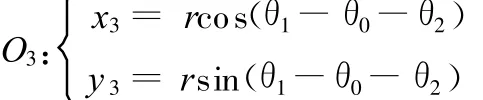
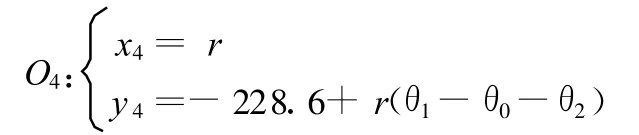
则

借助MATLAB可求解出第三阶段X2、Y 2的解析式:
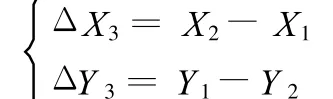
由式(1)得出

2.4 运动第4阶段
π <θ1≤θ0+(θ2+π)/2时,O1做竖直向下运动,O2做半径为r的圆弧运动,储药斗1支轴中心A1做变直径的圆弧旋转。O3做半径为r的圆弧运动,O4继续做竖直向上运动,直至 A1与A2在同一水平线上,储药斗2支轴中心A2做变直径的圆弧旋转,在此运动过程中,A1点高于 A2点。O1~O4的坐标分别为
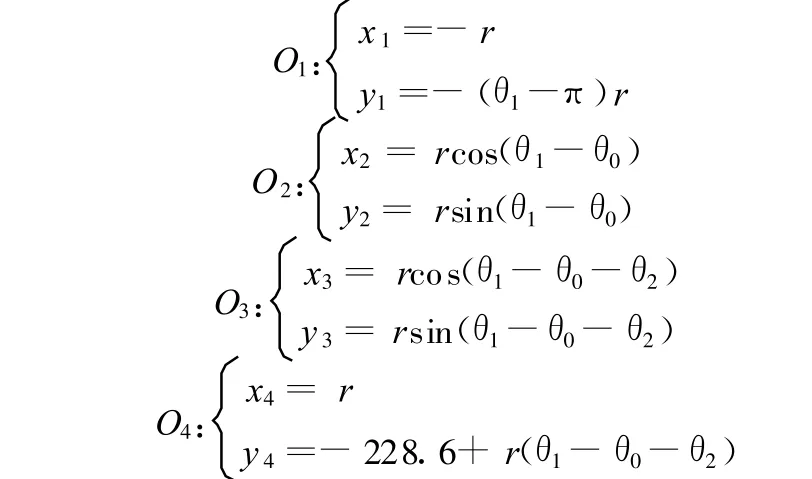
则
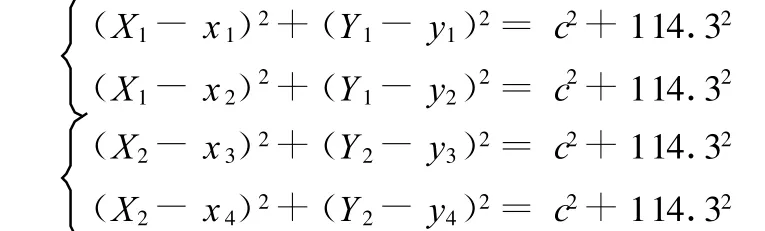
借助MATLAB,可求解出第 4阶段 X 1、Y 1、X2、Y2的解析式:
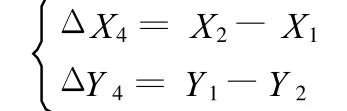
由式(1)得出

2.5 运动第5阶段
θ0+(θ2+π)/2 <θ1 ≤2θ0+θ2时 ,O1做竖直向下运动,O2做半径为r的圆弧运动,储药斗1支轴中心A1做变直径的圆弧旋转。O3做半径为r的圆弧运动,O4继续做竖直向上运动,直至O4与O在同一水平线上,储药斗2支轴中心A2做变直径的圆弧旋转。在此运动过程中,A2点高于 A1点,O1~O4的坐标分别与第4阶段O1~O4的坐标相同。
同理,借助MATLAB,可求解出第 5阶段X 1、Y 1 、X 2、Y 2 的解析式:
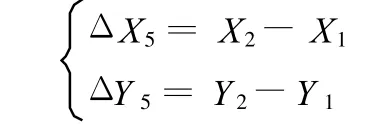
由式(1)得出

2.6 运动第6阶段
2θ0+θ2<θ1≤π+θ0时,O1做竖直向下运动,O2做半径为r的圆弧运动直至O2与O在同一水平线上,储药斗1支轴中心A1做变直径的圆弧旋转。O3、O4做半径为r的圆弧运动,储药斗2支轴中心A2沿半径为R的圆弧旋转。该过程可看作链轮顺时针旋转时,储药斗反向运动,其不干涉条件同运动第3阶段式(4)。
2.7 运动第7阶段
π+θ0<θ1≤π+θ0+θ2时 ,O1、O2做竖直向下运动,O3、O4做半径为r的圆弧运动直至O3与O在同一水平线上,储药斗1支轴中心A1做竖直向下运动。储药斗2支轴中心A2做半径为r+c的圆弧旋转。该过程可看作链轮顺时针旋转时,储药斗反向运动,其不干涉条件同运动第2阶段式(3)。
2.8 运动第8阶段
π +θ0+θ2 <θ1 ≤π+2θ0+θ2时 ,O1 、O2、O3做竖直向下运动,O4做半径为r的圆弧运动直至O 4与O在同一水平线上,储药斗1支轴中心A1做竖直向下运动。储药斗2支轴中心A2做变直径的圆弧旋转。该过程可看作链轮顺时针旋转时,储药斗反向运动,其不干涉条件同运动第1阶段式(2)。
3 基于运动不干涉条件的链传动优化设计
3.1 链传动优化的数学模型
3.1.1 优化设计思想
回转立体库占地面积是指钢结构框架外轮廓的投影面积,其长度方向受储药斗长度等因素的影响,其宽度方向受储药斗回转半径、储药斗宽度等因素的影响。当储药斗设计完成后,储药斗的宽度w和高度h已定,则在链传动的设计过程中,选定链条节距后,采用优化设计,适当选取支撑杆外伸量c和链轮节圆半径r,能获得最小的储药斗回转半径,使钢结构框架宽度最小,在其长度不变的前提下,减小占地面积,同时可以减小钢结构横梁的受力变形。
3.1.2 设计变量及目标函数
影响立式回转药柜链传动的因素有很多,根据储药斗运动不干涉条件的分析,θ1是独立的变量,另外引入系数λ,令c=λr,则可确定λ和r为变量,由此可知:
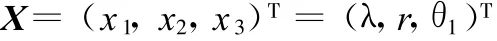
为使钢结构框架宽度最小,目标函数取储药斗回转半径L,即支撑杆外伸量c和链轮节圆半径r之和:
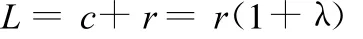
由上式可知,优化设计目标函数的表达式为
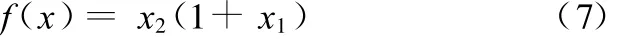
3.1.3 约束条件
(1)确保左右两侧储药斗直线运动不干涉条件为
2L≥w+A+2s
根据研究对象的具体设计可知w=420mm,A=30mm,s=87mm,由于 L=c+r=r(1+λ),所以
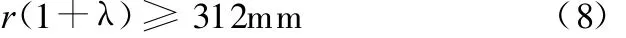
(2)立式回转药柜中储药斗将力作用在支撑杆上,使链条运行中链板处于倾斜状态,为确保链条具有足够的强度,支撑杆外伸量不宜过长,设计中取150mm ≤c≤250mm,即
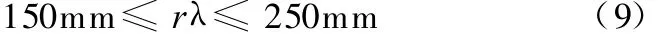
(3)由链传动分度圆计算公式
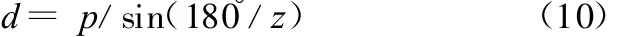
式中,p为输送链条节距,取p=12.7mm;z为链轮参数,取40~60。
所以
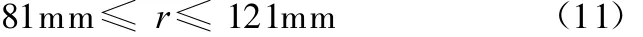
(4)垂直运动的两相邻储药斗支轴中心距离H的确定。由于链条节距p=12.7mm,垂直运动的两相邻储药斗支轴中心距离 H即单斗链条长度必须满足以下条件:

式中,h0为竖直运动的相邻两储药斗之间的间隙,一般h0≥3mm。
根据链条结构可知H=np(n为单斗对应的链节数)。
储药斗高度 h=275mm已知,可求得n≥22,选n=22,链条链节总数为 264。所以H=279.4mm。
(5)θ0 、θ2 分别为
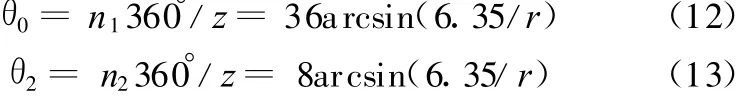
式中,n1为O1、O2之间对应的链节数;n2为O2、O3之间对应的链节数。
(6)由式(9)和式(10)可以推出
1.24 ≤λ≤3.08
(7)θ1的范围为

3.1.4 数学模型
综上所述,将变量 x1、x 2和 x3代入式(7)~式(9)、式(11)~式(13),则基于储药斗运动不干涉条件链传动优化数学模型表达为
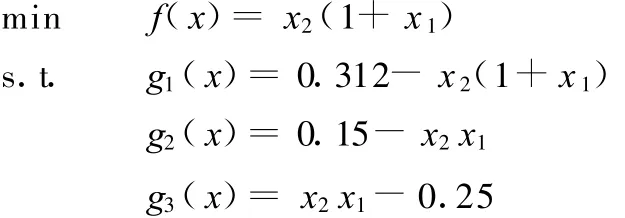
当0 ≤θ1≤θ0时,由式(2)得

当 θ0 <θ1 ≤θ0+θ2时,由式(3)得
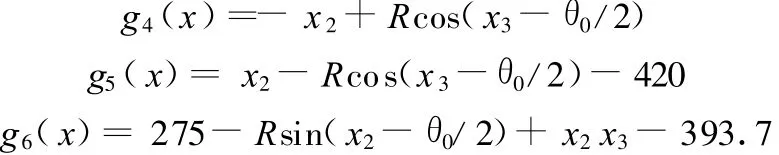
当θ0+θ2<θ1≤π时,由式(4)得
g4(x)=-ΔX3,g5(x)=ΔX3-420,g6(x)=275-ΔY3
当 π<θ1≤θ0+(θ2+π)/2时,由式(5)得
g4(x)=-ΔX4,g5(x)=ΔX4-420,g6(x)=275-ΔY4
当 π <θ1≤2θ0+θ2时 ,由式(6)得
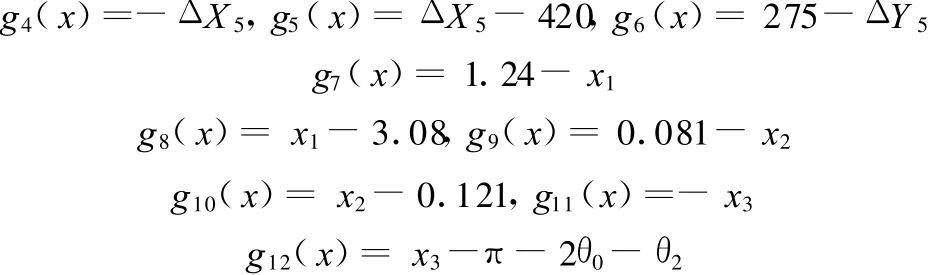
3.2 MATLAB优化求解
由数学模型可以看出,该优化设计属于有约束非线性优化问题。求解约束非线性优化问题的MATLAB函数是fmincons[5]。
MATLAB程序计算结果如下:
λ=1.7609,r=113mm,Lmin=312mm
由r值及式(10)可计算出z=55.88。因链轮齿数为离散变量,须对计算结果进行圆整,选择z=56,则 d=p/sin(180°/z)=226.5mm,即r=113.25mm。
由L=c+r可取c=199.5mm,则储药斗回转半径L=312.75mm,优化设计完成。
根据优化设计结果链条节距为12.7mm,支撑杆水平外伸量为199.5mm,每个储药斗对应链节数为 22,链节总数为 264,节圆直径为226.5mm,链轮齿数为 56,计算链条长度为3352.8mm,理论中心距为1320.8mm。
4 平衡杆导轨布局设计
通过对储药斗运动不干涉条件的分析,储药斗吊点的运行在固定于传动链上的支撑杆规定的轨迹中运行,所以储药斗吊点在回转曲线部分的运行轨迹可以由A1或A2的坐标解析解确定。由于单侧的平衡杆与储药斗的垂直中心线的角度为30°,所以平衡杆导轨的滚轮中心的坐标解析解可由下式求出:
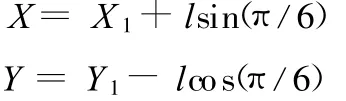
式中,l为平衡杆长度;X1为储药斗吊点x轴坐标;Y1为储药斗吊点y轴坐标;X为平衡杆滚轮中心x轴坐标;Y为平衡杆滚轮中心y轴坐标。
下面研究单个储药斗在保持水平状态下运动过程中平衡杆的运动规律。如图4所示,当储药斗吊点由位置1逆时针运行到位置2时,支撑杆1、支撑杆2之间的角平分线与垂直中心线的夹角为30°,且与平衡杆重合,我们把此时平衡杆导轨的滚轮中心所处位置称为翻转点。

图4 平衡杆滚轮中心翻转点位置示意图
当储药斗吊点继续逆时针旋转一微小角度由位置2运行到位置3时,如图5所示,我们以储药斗吊点为圆心、平衡杆长度为半径作一圆,此圆与平衡杆导轨中心线交于两点,分别位于支撑杆1、支撑杆2之间的角平分线两侧。这表明储药斗吊点由翻转点位置继续逆时针旋转时,平衡杆运动存在两种可能:如果平衡杆向角平分线左方运动,则储药斗保持水平状态,如图5中虚线所示;如果平衡杆向角平分线右方运动,则储药斗发生翻转,无法保持水平状态,如图5中实线所示。由于平衡杆导轨与平衡杆滚轮存在摩擦力,致使平衡杆向角平分线右方运动,储药斗发生翻转。
为了使储药斗顺利地通过翻转点并保持水平状态,必须采取适当的措施,这里采用将右侧平衡杆与垂直中心线保持30°、左侧平衡杆与垂直中心线保持-30°,从而使左右侧平衡杆导轨中心线对称于两链轮中心连线,如图6所示。
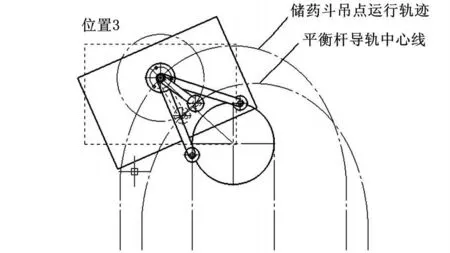
图5 储药斗翻转示意图
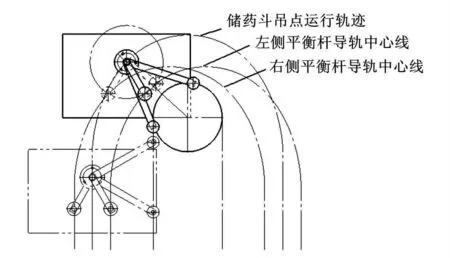
图6 右侧平衡杆通过翻转点示意图
当右侧平衡杆经过翻转点位置时,右侧平衡杆在左侧平衡杆带动下克服右侧平衡杆导轨与右侧平衡杆滚轮之间摩擦力,保持与左侧平衡杆同步,从而使储药斗顺利地通过翻转点并保持水平状态,反之亦然。
由图7可以看出,当左右两侧平衡杆分别与垂直中心线保持-30°、30°时,左右两侧平衡杆滚轮中心共有4个翻转点位置,由于平衡杆导轨偏中心对称布置,故当一侧平衡杆滚轮中心经过翻转点时,同一储药斗上另一侧平衡杆滚轮中心已错开翻转点,从而使两侧平衡杆保持同步并顺利通过翻转点。
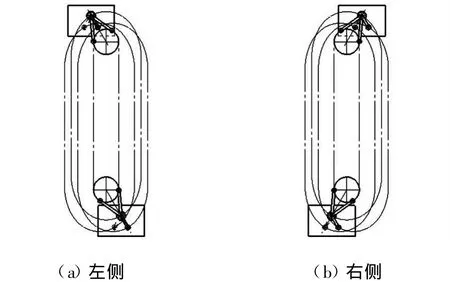
图7 左右两侧平衡杆滚轮中心翻转点位置示意图
5 基于UG和ADAMS的运动仿真分析
根据链传动优化设计结果,利用UG/Model建立链轮、链条、储药斗及支撑杆等模型,建立如图8所示的储药斗运动分析实体模型。模型由两侧链轮、两侧链条(各由44个链节组成)、4组支撑杆、2个储药斗组成。
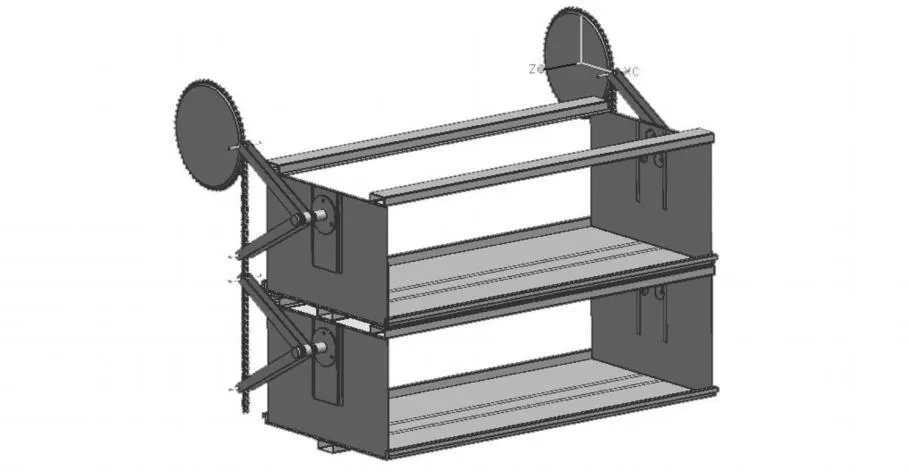
图8 链传动运动分析实体模型
因为本节重点研究储药斗不发生干涉的情况,所以只要求链轮链条有啮合运动即可,而不必让系统做周期运动,这并不影响对储药斗不干涉情况的研究。
在UG/Model模块中完成各个零件的建模且装配完毕后。进入 UG/Motion模块,把每一个零件定义为一个连杆,共100个连杆,为了方便以后加约束,从第1个链节开始在内外链节装配面的两圆心处定义标记点A001、A002,其Z轴垂直于装配面指向外。在第2个链节的装配面的两圆心处定义标记点A003、A004,依此类推,可以得到176个标记点。然后把链传动模型导入到ADAMS中。
由于链节数太多,逐个添加旋转副和接触副不太现实,因此编写宏命令来完成。宏命令是ADAMS/View的命令集,它可用来执行一连串的命令,通过使用条件循环命令,可以完成重复性操作。用宏MACRO_1创建链节之间旋转副和摩擦[6]。
同理,用宏MACRO_2创建链节和约束线之间的88个点线约束副,保证链条按预定轨迹运动,为保证储药斗在运动过程中保持水平,需添加储药斗与大地之间的2个垂直副,同时,建立支撑杆与链节、储药斗之间的14个旋转副,链轮与大地之间的2个旋转副,约束线与大地之间的2个固定副,链节与大地之间的2个平面副,合计196个约束副。以上设置见图9。
对链轮与大地之间的旋转副施加运动,设置仿真运行参数,仿真时间设为 8.43s,帧数为1000。仿真运行从第1帧到第1000帧,两储药斗在运动仿真过程8个阶段全部按预定轨迹从右侧运动到左侧,直至仿真过程结束,无干涉现象发生。
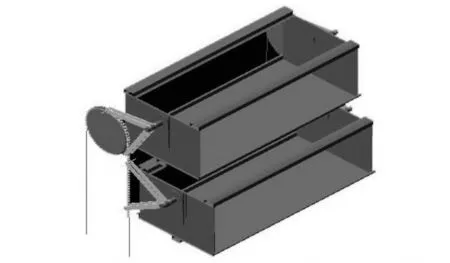
图9 储药斗运动分析仿真模型
根据运动仿真干涉检查结果可知,基于储药斗运动不干涉条件的链传动优化设计结果(储药斗回转半径 L=312.75mm,支撑杆水平外伸量c=199.5mm)可行,优化设计成功。
6 结论
分析了立式回转药柜链传动工作原理,建立了储药斗运动不干涉条件,利用MATLAB对传动系统进行了结构优化,给出了平衡杆导轨的合理布局方式,最后根据优化结果对储药斗进行运动仿真。目前立式回转药柜已投入运行,系统各部分运行正常,运行状态良好,达到了预期目的。证明上述结构设计正确可行。
[1] 刘文亮.基于SolidWorks的数控回转立体库的自动设计[D].济南:山东大学,2005.
[2] 郭鹏.基于CAE的垂直循环立体车库结构设计研究[D].济南:山东大学,2007.
[3] 郑志峰.链传动设计与应用手册[M].北京:机械工业出版社,1992.
[4] 王吉忠.垂直循环停车设备托架运动不干涉条件[J].机械,2005,32(3):22-23.
[5] 苏金明,张莲花,刘波.M ATLAB工具箱应用[M].北京:电子工业出版社,2004.
[6] 李军,刑俊文,覃文浩.ADAMS实例教程[M].北京:北京理工大学出版社,2002.
