BLADE刀锋技术详解

翁得河

本文结合模拟和实际例子，讲述BLADE的运动校正方法，图像重建的步骤及其目的。最后讨论与临床密切相关的扫描时间问题，同时介绍BLADE的序列的优缺点。

1 数据采集

BLADE刀锋序列，又称为螺旋桨序列PROPELLER[1]。其采集数据方式与TSE序列相似，不同之处在于每次采集数据时，TSE总是在笛卡尔坐标上进行相位和频率编码，如图1所示，每次激发之后，相隔一定行数采集一行k空间数据，总共采集n行数据(n=Turbo Factor，即快速因子)；刀锋序列则每次激发后都采集m行k空间中心数据(m=Turbo Factor)，且相邻两次数据采集旋转一定角度θ，如图2，旋转的圆心为k空间中心，该角度的计算公式如(1)

式中M为图像分辨率(Base Resolution)，BC为覆盖率(BLADE Coverage)，由公式可得出，在一定快速因子情况下，旋转角度和BC成反比，即BC越小，旋转角度越大。从图2同时可看出，BLADE采集的相位编码方向随着旋转角度的变化而变化，因此，其FOV永远为圆形，不像笛卡尔坐标下的FOV，可为长方形或者正方形。

除了用类似于TSE序列采集数据外，还可以用基于TGSE(GRASE)的Turboprop[2]序列或者基于EPI序列采集BLADE数据，这两种方法旨在提高扫描速度，但由于需要更加复杂的相位纠正方法，所以在临床上尚未得到广泛应用。

2 运动纠正

BLADE序列在k空间重复采集数据，这些冗余的数据除了用于重建图像增加信噪比外，还可以用来纠正成像物体在扫描过程中的刚性运动，即旋转和平移。

3 旋转校正

图像旋转一定角度，由傅立叶变换原理知，在k空间上也对应地旋转相同角度，且k空间数据的幅值不受平移运动影响，因为图像的平移在k空间上只表现为一定的相位变化，利用这个性质，可以把平移和旋转运动“分离”。图3A和3B模拟了一个旋转运动的情况，图3A是没有旋转的参考图像，图3B是以图像中心为圆心旋转30°后的图像，图3C为图3A变换到k空间后的图像，图3D为图3B对应的k空间图像。为了显示方便，k空间的数据都取自然对数，从图3C和图3D可以看出，图像上旋转的角度，确实与其对应k空间上旋转的角度一致。

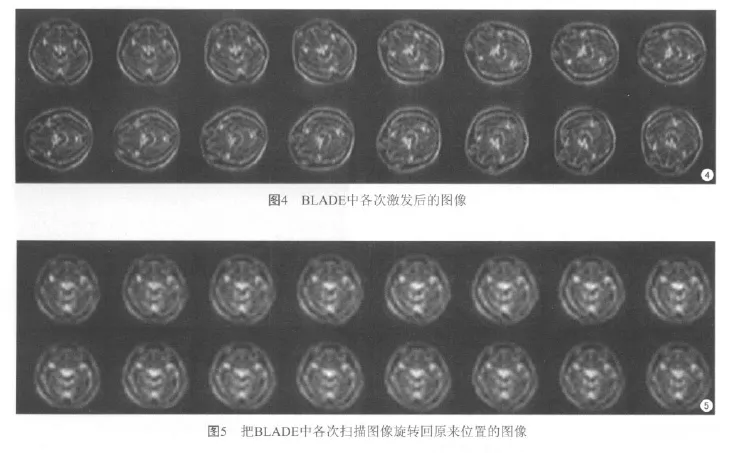
在BLADE序列的运动纠正算法中，首先把各次扫描的数据变换到图像域，得到低分辨率的图像，如图4所示；然后按照序列中规定好的旋转角度，把图像旋转到真实的位置，如图5所示。把旋转后得到的所有图像平均，得到的图像作为参考图像，其他图像与其进行比较后，计算出运动角度。

计算旋转角度的方法大概分为两种：一种为互信息法，即把运动图像旋转一个小角度，求旋转后图像与参考图像的互相关性，在一定角度范围内变换旋转角度求互相关性，最后把相关性最大所对应的旋转角度作为该图像的旋转运动角度。

另外一种为傅立叶-梅林变换法(Fourier-Mellin transform)，即对参考图像和运动图像进行傅立叶变换，得到如图3C和图3D类似的k空间图像，然后对k空间图像进行梅林变换。梅林变换实际上是一种坐标变换，把图像从笛卡尔坐标变换到极坐标。k空间在笛卡尔坐标上的旋转，极坐标表现为图像平移。对图像位移的检测，比用互信息法检测旋转更加方便，并可借助傅立叶变换快速求得图像平移量，从而得到旋转角度。

傅立叶变换法求图像位移主要利用傅立叶变换的相位性质，即在图像域上的位移，k空间上表现为沿位移方向均匀变化的相位，相位的大小与位移成正比。

由此，可把梅林变换后的图像再次进行傅立叶变换，用公式(2)求得旋转图像和参考图像k空间相位的互相关函数，如图6所示。检测这个二维函数的最大值所在位置可得两幅图像之间的相对位移，对于刚性旋转而言，只需检测角度方向的位置，并根据位移转换成旋转角度。

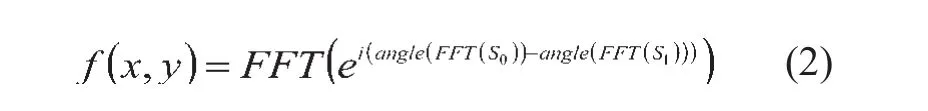
式中f()为互相关函数，FFT()为傅立叶变换，angle()为取角度算子，S0、S1分别表示参考图像和旋转图像的傅立叶-梅林变换图像。

4 位移校正

在求得旋转角度之后，可对图像进行旋转校正，校正后的图像只剩下位移。求位移的算法与上述相同，用傅立叶变换求互相关函数。得到旋转和位移参数后，便可对图像进行重建。

5 图像重建

图像的重建主要有三种方法：重排法，直接变换法[3,4]和迭代法，因为直接变换法和迭代法耗时长，尚不能在临床上使用，本文只介绍重排法，首先介绍参考文献[1]的方法。重排法大概步骤如下：

(1)相位纠正：BLADE采集数据时，k空间上旋转的圆心并不总是k空间中心，由此引入了额外误差，假如不做任何纠正，重建后图像有些区域可能出现相位相消而导致信号缺失。对于圆心不在k空间中心的数据片，相当于在k空间上有位移，根据傅立叶变换性质，对应到图像上为增加了沿位移方向线性变化的相位，相位纠正的目的是把这个线性变化的相位剔除。线性变化的相位可近似地由原始数据乘以一个金字塔形滤波器，再变换到图像域获得。把原始数据也变换到图像域，减掉获得的线性变化相位即可完成相位纠正。

(2)密度补偿函数：由于BLADE采集时，k空间填充的密度不一样，中心填充的密度大，越往四周，填充密度越小。所以，重排前，必须对所有数据进行补偿，即根据数据所处k空间位置，计算一个系数乘到数据上。密度补偿函数的计算取决用于重排的窗函数以及数据在k空间的分布，通常的函数为凯瑟贝塞尔窗(Kaiser Bessel window)，同时还需考虑数据所对应的旋转运动角度。密度补偿的目的是数据重排后，在笛卡尔坐标上的每个数据点的加权与笛卡尔采集的数据一样都为1。

(3)数据重排：运动纠正后的数据经过相位纠正后，被重新变换到k空间，此时用一定宽度的卷积窗(即一个二维的小矩阵，比如3×3)，以每个笛卡尔坐标为中心，求中心周围(在窗宽范围内)数据的加权和，权重为数据对应的密度补偿函数，得到笛卡尔坐标下的重排数据。对数据施加傅立叶变换，得到最终图像。

(4)信号均匀校正：数据重排时对数据进行加窗操作(卷积窗)，影响重建后图像亮度的均匀性。由于k空间的卷积操作，相当于图像域上给图像乘上一个加权图。因卷积窗宽有限，所以加权窗并不均匀，而是中间权重大，四周权重小。均匀度校正根据卷积窗，算出相应图像域的加权图，把加权图从重建后的图像除掉，便可得到亮度均匀的图像。

除了以上的重排算法外，还可采用插值法，把k空间数据全部旋转回原来位置后分别进行傅立叶变换，把得到的所有图像相加获得最终图像，称为旋转重建法。该重建法与以上介绍的重排法等效，但因为是图像域相加，固能进一步降低运动伪影。

6 扫描时间及讨论

众所周知，一定分辨率M下，BLADE的扫描时间比TSE的长，TSE和BLADE在快速因子TF一定时所需要的激发次数N可以用公式(3)、(4)表示。

下面通过一个例子，以TSE扫描时间为参考来讨论BLADE扫描时间。假设图像的分辨率为256，Turbo Factor (TF)=29，TR=4秒。对于TSE序列，扫描一幅图像需激发9次，用时36秒。而当Blade Coverage (BC)=100%时，BLADE序列需要激发14次，用时56秒，为TSE时间的1.56倍。由于BLADE对k空间中心重复采集，其信噪比相对TSE高，为了提高成像速度，可减少BC值，如降到64.3%时可达到与TSE一样的扫描时间。利用并行采集也可降低扫描时间。与前面BLADE一样参数，增加加速因子iPAT=2，参考线(Reference line)=8的情况下，等效的TF为52，这时所需激发次数减为8，总扫描时间为32秒。由此可见，在临床扫描时，可以结合BLADE本身的优点，合理设置参数，以获得更好的时间效率。

BLADE除了能纠正刚性运动伪影外，对于非刚性运动，比如腹部成像时的呼吸运动，也有减弱的作用，因为BLADE采集相位编码方向的运动伪影随着编码方向旋转而旋转，不像笛卡尔坐标下的TSE采集，总在一个方向出现，所以重建后得到的图像伪影不如TSE明显，当然图像会或多或少地模糊。旋转重建方法能更好降低非刚性运动对图像的影响，从而得到较好的临床腹部图像(图7)。

BLADE的最大缺点在于扫描层面方向，一般来说，只适合于横断位扫描。矢状面和冠状面扫描只能通过增加相位过采样来避免卷拆伪影(BLADE图像表现为带状伪影)，但增加了扫描时间。将来可能的解决方案是采用二维激发方式，只激发层面内特定范围，而不是整个层面。到目前为止，BLADE不能纠正平面间的运动，使其应用受到极大限制，临床扫描时可借助生理信号或者导航信号(PACE功能)等减少运动伪影。

[1]Pipe JG. Motion correction with PROPELLER MRI:application to head motion and free-breathing cardiac imaging. Magn Reson Med, 1999, 42(5):963-969.

[2]Tamhane AA., Arfanakis K. Motion correction in periodically-rotated overlapping parallel lines with enhanced reconstruction (PROPELLER)and turboprop MRI. Magn Reson Med, 2009, 62(1):174-182.

[3]Fessler JA, Sutton BP. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Tran Sign Proc, 2002,51(2):560-574.

[4]Sarty GE., Bennett R, Cox RW. Direct reconstruction of non-Cartesian k-space data using a nonuniform fast Fourier transform. Magn Reson Med, 2001, 45(5):908-915.