基于磁流变阻尼固紧器的工作台定位研究

余晓芬 马文平 程伶俐

合肥工业大学,合肥,230009

0 引言

磁流变液由导磁性颗粒、载液和添加剂组成,它在外界磁场作用下能在毫秒级时间里从自由流动的牛顿流体转变为Bingham类固体,并且这种变化是完全可逆的。磁流变阻尼固紧器是一种利用磁流变液提供可控阻尼固紧力的控制装置,具有能耗低、出力大、响应速度快、结构简单、阻尼力连续可调、与计算机控制结合方便等优点,目前已广泛应用于建筑结构、振动控制、机械传动等领域[1-7]。这些应用的本质共同点是磁流变阻尼固紧器具有无冲击特性。

常用的固紧方法有机械固紧和电磁固紧,但都带有冲击性,无法做到无冲击固紧,从而导致定位波动很大。利用磁流变阻尼固紧器辅助工作台进行纳米定位,一方面可实现柔性阻尼,减弱直线电机传递给工作台的振动;另一方面可无冲击固紧工作台,实现对工作台的纳米级精度定位。

1 磁流变阻尼固紧器的工作原理

图1为剪切阀式磁流变阻尼固紧器的工作原理图,该阻尼固紧器采用横向卧式结构,通过连杆与工作台相连,运动方向为水平方向。当线圈不通电时,磁流变液表现为具有一定黏度的牛顿流

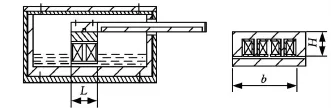
图1 剪切阀式磁流变阻尼固紧器原理图

体,阻尼固紧器可以自由移动;当线圈通电后,在其周围产生磁场,磁流变液由牛顿流体瞬间变为Bingham类固体[8],使流体流动的阻尼力增加,阻尼固紧器的运动受阻;当阻尼力足够大时,阻尼固紧器可被锁紧,从而固紧工作台。剪切阀式剪阻尼固紧器兼具了剪切式固紧器和阀式固紧器的特点,且阻尼固紧力相对较大,其阻尼力可以表示为剪切式阻尼力和阀式阻尼力之和,即[8]

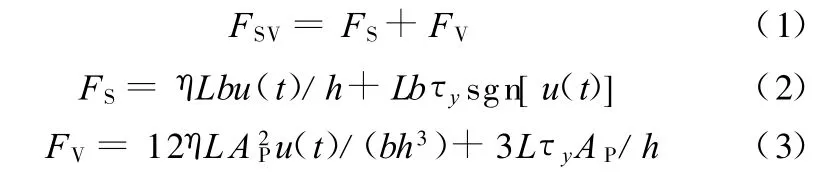
式中,FS为剪切式阻尼力(黏滞阻尼力);FV为阀式阻尼力(库仑阻尼力);τy为磁流变液的剪切屈服应力;η为磁流变液的动力黏度;L为活塞的长度;b为磁芯的宽度;h为磁芯与阻尼固紧槽的间隙;u(t)为磁流变液的流速;AP为磁芯的有效横截面积,AP=Hb;H为磁芯的高度。

经论 证：∂FSV/∂L ＞ 0, ∂FSV/∂b ＞ 0,∂F SV/∂h＜0,减小h可以增大阻尼力,但h太小,会增加阻尼固所紧器的制造难度,实际设计中h通常取1～2mm[8]。

2 X向、Y向磁流变阻尼固紧器的设计

2.1 结构设计

图2是自行设计制作的X向、Y向磁流变阻尼固紧器的结构图,该装置采用了横向卧式结构。内部的两个电磁线圈通过螺纹结构与磁芯相连,并一起装于阻尼固紧槽中。外部的隔磁槽与隔磁盖板形成隔磁系统。对称放置在工作台两端的磁流变阻尼固紧器通过连杆形成一体,线圈从连杆上的引线槽中引出。连杆与直线电机相连,电机与工作台相连,电机与工作台之间用4个套筒隔开,这不仅可以对电机的高度进行定位,还避免了阻尼固紧器直接与工作台的串联。与纵向立式阻尼固紧器相比,横向卧式阻尼固紧器具有以下优点：①磁流变液不需要充满,只需高出磁芯底部2～3mm即可,避免了磁流变液溢出和密封的问题。②导向由与工作台配合的导轨提供,节省了自身的导向机构。③消除了密封装置与连杆的摩擦力,使初始阻尼力能降到最小,可满足直线电机能正常驱动工作台的要求。

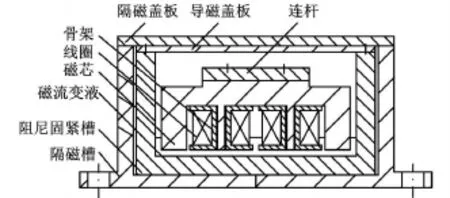
图2 X向、Y向磁流变阻尼固紧器结构图

2.2 磁路设计

根据磁流变阻尼固紧器磁路设计原则[9-12],我们将电工纯铁(DT4系列)作为线圈铁芯,将直径为0.6mm的电磁漆包线作为线圈。绕线之前在线圈骨架上涂上绝缘漆,以保证线圈与骨架的相对绝缘,最终测得线圈的电阻为0.65Ω,将对称放置的阻尼固紧器的 4个线圈串联(总电阻为2.60Ω)。

如图3所示,箭头方向表示磁路方向,磁场方向与磁流变液的流动方向垂直,磁流变阻尼固紧器的磁路包括5个部分：阻尼固紧槽1、磁流变液2、线圈骨架3、线圈支架横向段4、线圈支架纵向段 5,其磁导率如下 ：μ1=1.26 ×10-3H/m,μ2=1.01 ×10-5H/m,μ3=μ4=μ5=8.82 ×10-3H/m。

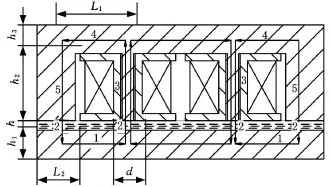
图3 X向、Y向磁流变阻尼固紧器磁路图

根据磁路基尔霍夫定律(一)有

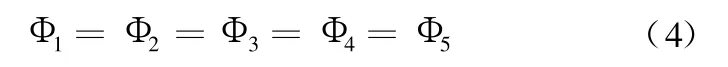
图3中各部分磁阻为

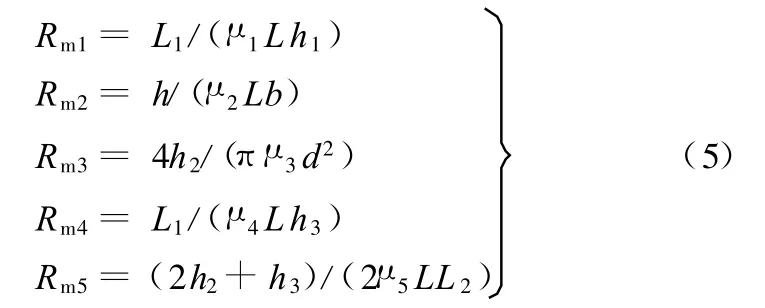
根据阻尼固紧器各结构参数对阻尼力的影响,对阻尼固紧器的结构尺寸进行优化,结果如下：h1=6mm,h2=14mm,h3=6mm,L 1=15mm,L2=8mm,h=2mm,b=60mm,L=20mm,d=6mm。将其代入式(5)得

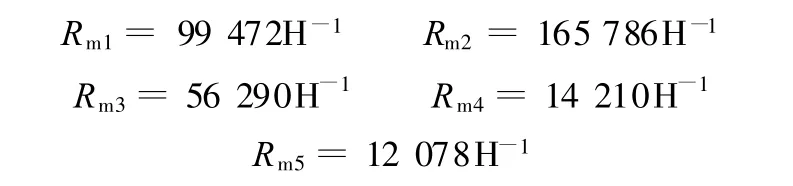
总磁阻

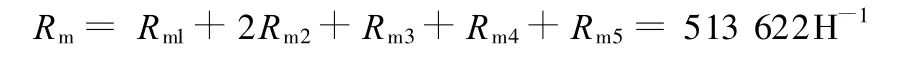
设计磁路时应保证磁芯与阻尼固紧槽间隙中的磁流变液在达到磁饱和时,磁芯和阻尼固紧槽都未达到磁饱和状态。磁流变液在0.6～0.8T时达到磁饱和,此时磁路中各部分的磁通量都为

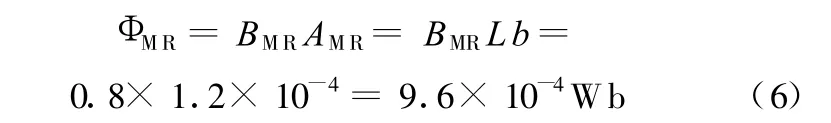
根据磁路基尔霍夫定律(二)有

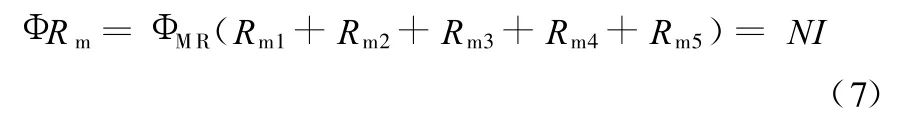
线圈所能承受的最大电流为2A,将各参数值代入式(7),解得匝数 N=246.539,考虑到磁场在空气中的损失,取N=250。

3 磁流变阻尼固紧器与工作台配合的定位实验

对自行设计的X向、Y向磁流变阻尼固紧器进行标定,测得其特性曲线如图4所示,阻尼力范围为4～51N。

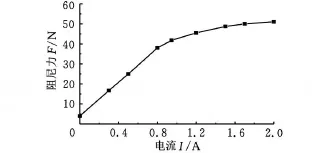
图4 X向、Y向磁流变阻尼固紧器阻尼力特性图

图5 所示为自行研制的纳米三坐标测量机的二维工作台,左右对称放置了两个磁流变阻尼固紧器,通过连杆将阻尼固紧器、直线电机和工作台间接连接。位移测量装置为光栅位移测量装置,其硬件组成包括：15位200k Hz的A/D转换卡、光栅栅距W=20μm的光栅尺、光栅头 RGH25F、光栅传感器RGS20-S。通过光栅快速细分算法和光栅信号采集处理方法[13-14]使光栅位移测量系统具有以下特性指标：最大测量速度v max=133mm/s,稳态变化量为0.1nm,测量分辨率为1nm,精度为4nm。

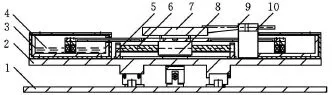
图5 纳米三坐标测量机二维机械结构图

实验中将光栅尺贴在与 X向工作台相连的斤板上,在小于1mm间距的位置放置光栅头,纳米工作台由型号为TB1102的TPMLSM-圆筒形永磁直线同步电机(采用单极驱动方式)驱动。工作台的整个行程分为驱动和定位两个阶段,在驱动阶段不加电流或加小电流,提供很小的初始阻尼力,保证工作台的正常运行,并且这种阻尼力是柔性可调的;在定位阶段加大电流,以提供足够的固紧力锁紧工作台。实验中以2mm为步距进行驱动定位,走完100mm行程,驱动速度设定为3mm/s,将起始点位置作为0位移点,以后每走一个步距,位移增加2mm。实验中在驱动控制程序里设定记录数据个数为2000,采集的实验数据均以*.txt形式存储,取最后稳态条件下的100个数据计算标准差σ,计算公式为

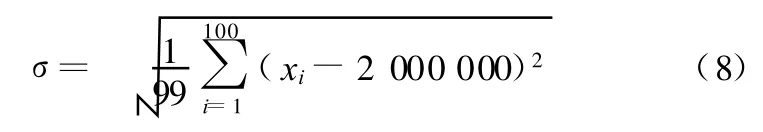
理论位移值为2mm,实际位移值xi是定位阶段在2mm处波动的位移值。将100mm位移50等分,以 2mm,4mm,…,100mm 为横坐标,以每个2mm处的定位标准差作为纵坐标作得图6和图7。

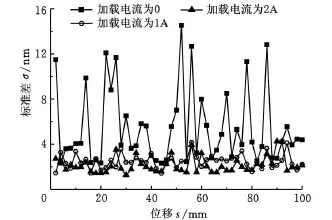
图6 正向行程加不同电流定位比较

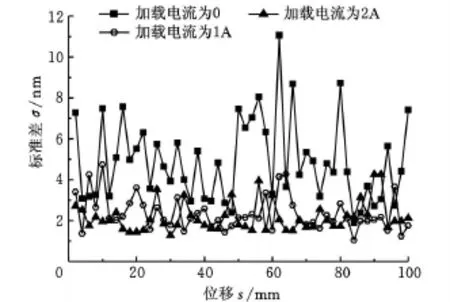
图7 反向行程加不同电流定位比较

从图6和图7中可以看出,正向行程比反向行程的定位效果好,加载电流1A、2A后定位更加稳定,定位波动均在5nm以内。定位实验中磁流变阻尼固紧器加载电流时计算出的标准差要比不加电流时的标准差小,在某些位置差值已经达到12nm,这充分证明了在直线电机驱动工作台运动过程中,磁流变阻尼固紧器对于定位起到了作用;当电流从1A增大到2A时,标准差略微有所减小,减小幅度下降;结合图4可知,阻尼固紧器的阻尼力在电流大于等于1A时增加幅度也明显减小,说明此时磁流变液已开始进入饱和状态。从图8中可以看出：直线电机的驱动速度对定位影响不大(已用往复运动实验论证[15]),阻尼固紧力直接影响定位精度。

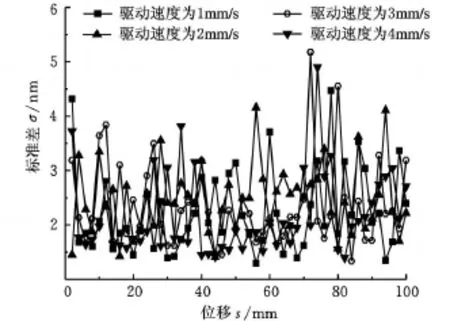
图8 正向行程不同驱动速度定位比较

4 结论

(1)所设计的磁流变阻尼固紧器输入电压范围为0～5.2V,输出阻尼力范围为4～51N,最大固紧力为51N。

(2)采用了新颖的横向卧式结构,解决了以往纵向式阻尼固紧器磁流变液溢出密封和摩擦导致初始阻尼力较大的问题,导向由导轨提供,节省了自身的导向机构。

(3)工作台不加阻尼固紧器时的定位波动约为20nm,加上阻尼固紧器后在不加电流时约为12nm,加载2A电流时波动已减小到5nm以内,减弱了直线电机驱动时传递给工作台的振动,降低了直线电机整个驱动行程中的波动。

(4)减小了传统机械、电磁固紧方法带来的冲击,并最终实现了工作台的无冲击固紧,减小了纳米级定位波动。

[1] Wang Juan,Hu Hongsheng,Wan Jiong,et al.Development of an Embedded Control System for Magnetorheological Fluid Damper under Impact Load[J].Electronic Measurement&Instruments,2009,19(1)：39-41.

[2] Zhu Tianjun,Zong Changfu.Development of MRF Damper Modelling and Validation of MRF Damper Test[J].Control Automation and Systems Engineering,2009,7(2)：238-241.

[3] Zapateiro Mauricio,Karimi Hamid Reza,Luo Ningsu.Semiactive Backstepping Control for Vibration Reduction in a Structure with M agnetorheological Damper Subject to Seismic Motions[J].Journal of Intelligent Material Systems and Structures,2009,20(17)：2037-2053.

[4] Guan Xinchun,Guo Pengfei,Ou Jinping.Study of the Response Time of MR Dampers[C]//Second International Conference on Smart M aterials and Nanotechnology in Engineering.Weihai,China,2009：74930u.

[5] Chen Jinxin.New Type of Magnetorheological Fluid Damper Applied to the Small Damping Force Condition[J].Journal of Vibration and Shock,2009,28(2)：155-161.

[6] Hu Wei,Wereley N M,Chemouni L,et al.Semiactive Linear Stroke Magnetorheological Fluid Elastic Helicopter Lag Damper[J].Journal of Guidance,Control,and Dynamics,2008,30(2)：565-575.

[7] Chooi Weng Wai,Olutunde Oyadiji S.Experimental Testing and Validation of a M agnetorheological Damper Model[J].Journal of Vibration and Acoustics-Transaction of the ASME,2009,131(6)：141-147.

[8] 李志全,杜成斌,于国军,等.磁流变阻尼器阻尼特性试验与改进阻尼模型研究[J].振动与冲击,2009,28(5)：124-127.

[9] 周云,谭平.磁流变阻尼控制理论与技术[M].北京：科学出版社,2007.

[10] 阎照文.ANSYS 10.0工程电磁分析技术与实例解析[M].北京：中国水利水电出版社,2006.

[11] 吴球红,马平,陈振辉,等.大行程直线电机的磁流变阻尼器优化设计[J].机电工程技术,2008,37(9)：57-59.

[12] 郭鹏飞,关新春,欧进萍.磁流变液阻尼器响应时间的试验研究及其动态磁场有限元分析[J].振动与冲击,2009,6(5)：70-75.

[13] 徐从裕,余晓芬.非同步采样法的光栅纳米测量[J].计量学报,2008,29(4)：293-296.

[14] 徐从裕,余晓芬.基于互补函数算式的光栅快速细分方法[J].电子测量与仪器学报,2006,20(3)：6-9.

[15] 马文平,余晓芬,程伶俐,等.用于微纳米测量的磁流变阻尼固紧系统[J].应用科学学报,2010,28(1)：106-110.