DCT变速器双离合器压力最优控制方法的仿真研究

李瑜婷 赵治国 章 桐

同济大学,上海,201804

0 引言

双离合器自动变速器(double clutch transmission,DCT)是近年来备受关注的新型自动变速器,它在换挡过程中通过对两个离合器的协调控制,能保证变速器不间断地输出动力。DCT既继承了机械式自动变速器(automated manual transmission,AMT)结构简单、效率高的优点,又消除了AMT动力中断的缺点,实现了动力性换挡。因此,DCT较AMT具有更好的综合性能。

起步及换挡控制是DCT控制的主要内容,而对于起步、换挡品质的改善而言,双离合器的协调控制则起着至关重要的作用,也一直是DCT控制研究的难点和重点。本文基于DCT结构,建立了DCT起步、换挡动力学模型,利用线性二次型最优控制方法,分别对起步、换挡过程中离合器压力控制问题进行研究和仿真分析。

1 DCT动态模型

1.1 DCT变速器结构及工作原理

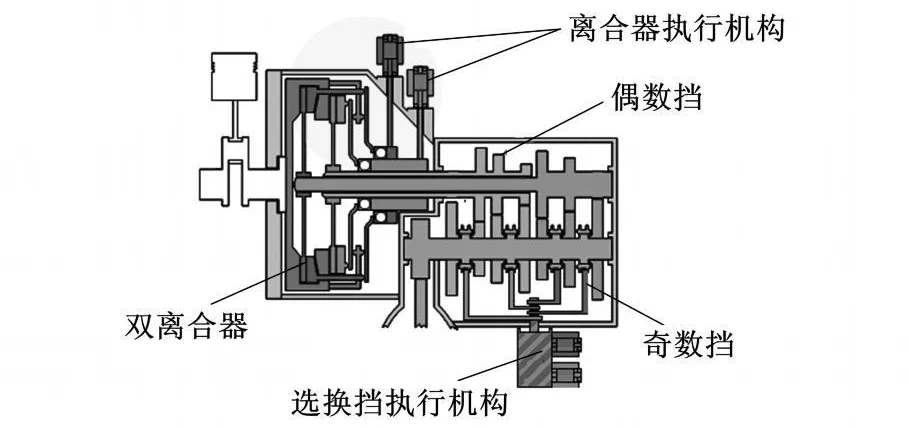
图1 某干式双离合器自动变速器结构示意图

某干式DCT结构如图1所示,发动机输出轴与双离合器相连,离合器1通过实心轴与奇数挡相连,离合器2通过空心轴与偶数挡和倒挡相连。发动机启动后,变速器挂上一挡,离合器1逐渐接合,发动机扭矩通过整个系统传递至驱动轮。当车速接近二挡换挡点时,第二挡已被预先选定,此时离合器2分离,不传递转矩。当变速器从一挡换到二挡时,离合器1逐渐分离,离合器2则逐渐接合,此时动力通过离合器1和离合器2共同传递到驱动轮,直至离合器2完全接合,同时,ECU会根据车速预先选定下一挡位(一挡或三挡),依此类推。

1.2 DCT模型的简化

根据DCT的结构及工作原理,将DCT简化为一个多自由度系统(图2),在简化过程中对模型作如下假设[1-2]：①忽略传动轴的径向振动及温度影响;②忽略轴承的轴承座弹性及齿轮的啮合弹性;③所有的机械损失均视为车辆阻力的一部分;④离合器视为干摩擦单元。

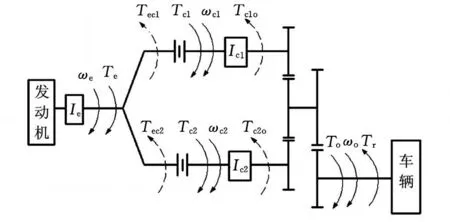
图2 DCT结构简图

1.3 DCT起步动力学模型

DCT起步过程可看作离合器1单独接合的过程,即 T ec2、T c2、T c2o均为零,发动机转矩通过离合器1及传动系统传递到驱动轮,由此可建立如下动力学模型：

起步模型中各参数间存在如下关系：

式中,be为发动机和离合器主动部分向发动机转化的阻尼之和;bc1为离合器1从动部分的阻尼;i1、i0分别为奇数挡传动比和主传动比;v为车速;δ为旋转质量换算系数;m为车辆质量;Fx为车辆行驶阻力;rw为车轮半径;F1为离合器1压力;μ1为离合器摩擦因数;R0、R1分别为离合器内外盘半径。

整理式(1)、式(2)可得

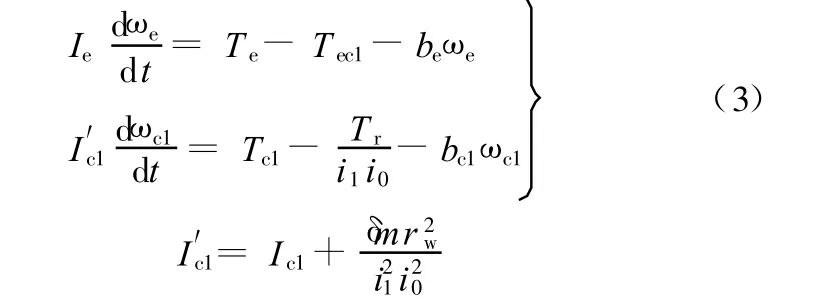
当离合器1完全接合时,起步过程完成,车辆在一挡运行,此时发动机转速与离合器1从动盘转速相同,即 ωe=ωc1,由此可根据式(3)得到车辆一挡运行时的动力学模型：

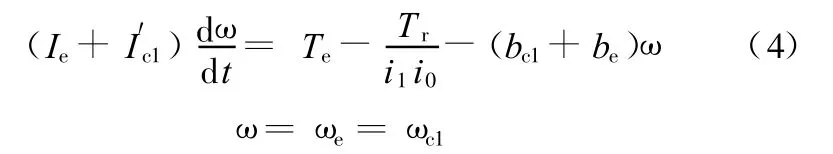
1.4 DCT换挡动力学模型

DCT换挡过程为离合器1与离合器2协调配合的过程,以一挡升二挡为例,换挡过程中离合器1分离,离合器2接合,发动机转矩通过离合器1和离合器2以及相应传动系统传到驱动轮。为了能更好地描述整个换挡过程中两个离合器各自的状态,以两个离合器的转速为状态变量,建立如下动力学模型：

换挡模型中各参数间存在如下关系：

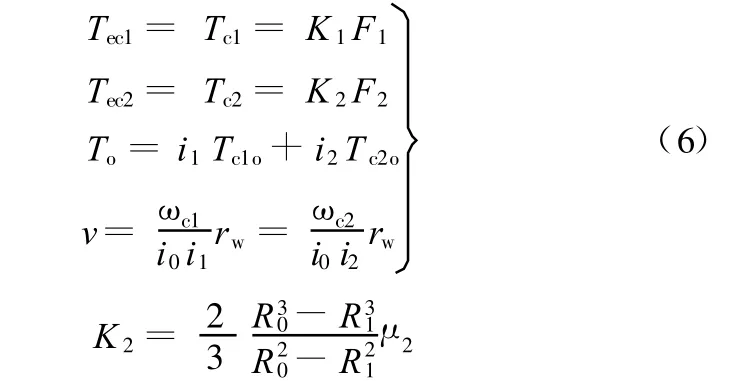
式中,bc2为离合器2从动部分的阻尼;i2为偶数挡传动比;F2为离合器2压力;μ2为离合器2摩擦因数。

整理式(5)、式(6)可得

当离合器2完全接合时,一挡至二挡升挡过程完成,车辆在二挡运行,此时发动机转速与离合器2从动盘转速相同,即ωe=ωc2,由此根据式(7)得到车辆二挡运行时的动力学模型：

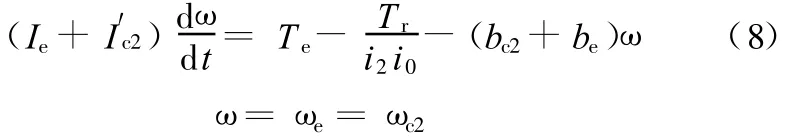
2 DCT双离合器压力最优控制

2.1 离合器接合品质评价指标

对离合器的接合过程有两项基本要求,一是接合要平稳,二是离合器使用寿命要长。接合平稳性的评价指标通常采用冲击度,而离合器使用寿命的评价指标则采用滑摩功[3]。

2.1.1 滑摩功

滑摩功W是指离合器在接合过程中,主从动摩擦片间滑动摩擦力矩所做的功[4],对两个离合器同时作动的DCT而言,滑摩功为

式中,tf为离合器接合完成时间。

在离合器接合过程中,滑摩功转换成热能被离合器吸收,使离合器温度升高,过高的温度将导致离合器磨损并引起热失效,因此在接合过程中必须要控制滑摩功的大小。

2.1.2 冲击度

冲击度是指汽车行驶过程中纵向加速度的变化率[4],即j=d2v/d t2。对于DCT而言,冲击度可表示为

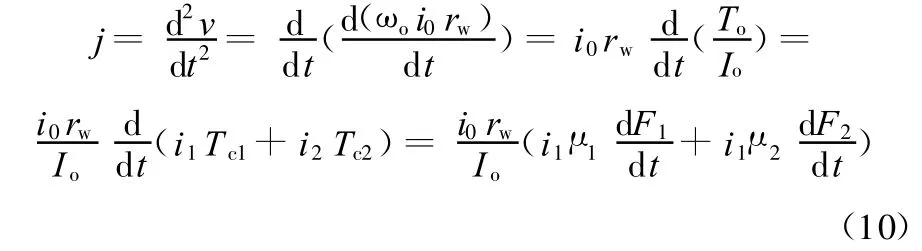
式中,Io为发动机输出端的转动惯量。

冲击度不仅可以真实地反映人对车辆纵向舒适性的感觉,还可以把道路条件所引起的弹跳和颠簸加速度等排除在外,如实地反映了起步换挡过程中汽车传动系统载荷及车辆运动状态的变化所引起的冲击。德国对于冲击度限定的标准为j≤10m/s3。

在换挡过程中,滑摩功和冲击度实际上是两个相互矛盾的评价指标,如减小滑摩功,则换挡时间缩短,冲击度就会增大,反之亦然。所以需要设计合适的控制策略使两者平衡,从而使离合器换挡性能达到最佳。

2.2 DCT起步离合器压力最优控制模型

本文采用线性二次型最优控制,对离合器起步压力进行控制。最优控制就是设计控制变量u(t),使状态变量X(t)由初态到终态的过程中,性能指标达到最小值。线性二次型最优控制指系统是线性的,性能指标函数是二次型的最优控制[5]。

DCT起步过程完成时ωe=ωc1,结合其起步动力学模型,依次选取 x1=ωe,x2=ωe-ωc1,x3=F1为状态变量,u1=d F1/d t为控制变量,根据式(3)得到控制方程

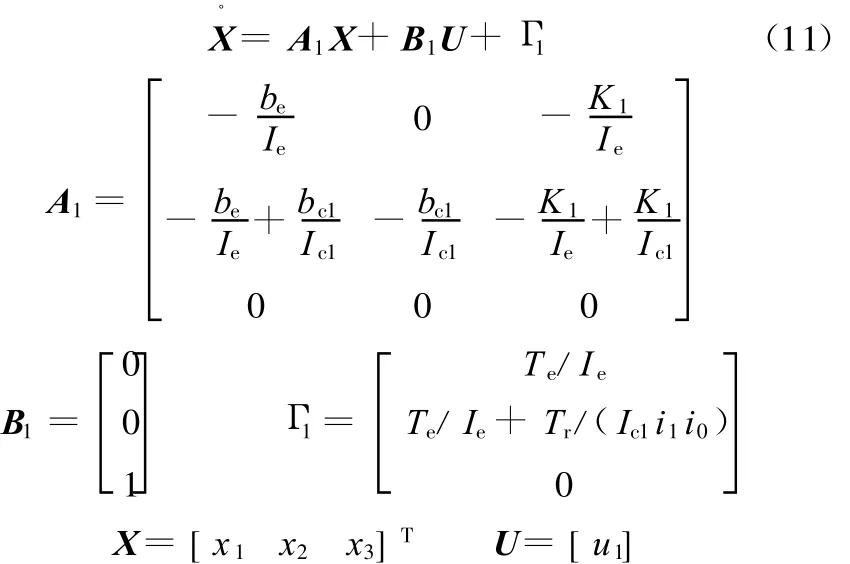
为了综合考虑滑摩功和冲击度对起步品质的影响以及使x2(t f)=0,选取

式中,q1、r1分别为所选取的加权系数。

则性能指标

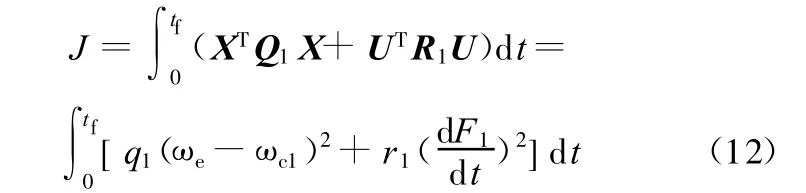
控制变量u(t)=R-1B(-P(t)X(t)+h(t)),其中,P(t)可通过求解黎卡提方程得到：

h(t)是为了补偿控制方程中的干扰项 Γ1而引入的补偿量,h(t)可通过下式求解[6]：◦

民族唱法和美声唱法相比听起来声音更加明亮，位置更靠前一些，这与中国传统的审美有关。它更多地使用口咽腔与头部的共鸣，声音集中靠前，讲究喉下换字，较之美声，“贴”得更紧。而且运用民族唱法时，喉部位置相对于美声唱法略高一些。民族唱法咽音成分比较少，这是因为在进行演唱时，声带只会缩短而没有变薄。由于中国语言的特点，民族唱法在歌唱时，要求发音集中在牙齿、唇等口腔靠前的部分比较多。

2.3 DCT换挡双离合器压力最优控制模型

以一挡升二挡为例,建立升挡时双离合器控制模型。在利用线性二次型最优控制方法对升挡过程中两个离合器进行控制时,因为最终系统状态是由输出扭矩T o所决定的,而T o=i1 T c1o+i2 T c2o,也就是说,只要两个离合器所传递的扭矩值使To不变,则达到的系统状态是相同的,在此情况下,两个离合器的压力值可以有许多种取法,因此便无法直接通过方程求解出两个离合器的最优压力。在本文中,根据一般经验,将两个离合器压力的变化速率设定为一定比例,由此对DCT升挡过程中的两个离合器压力进行控制。

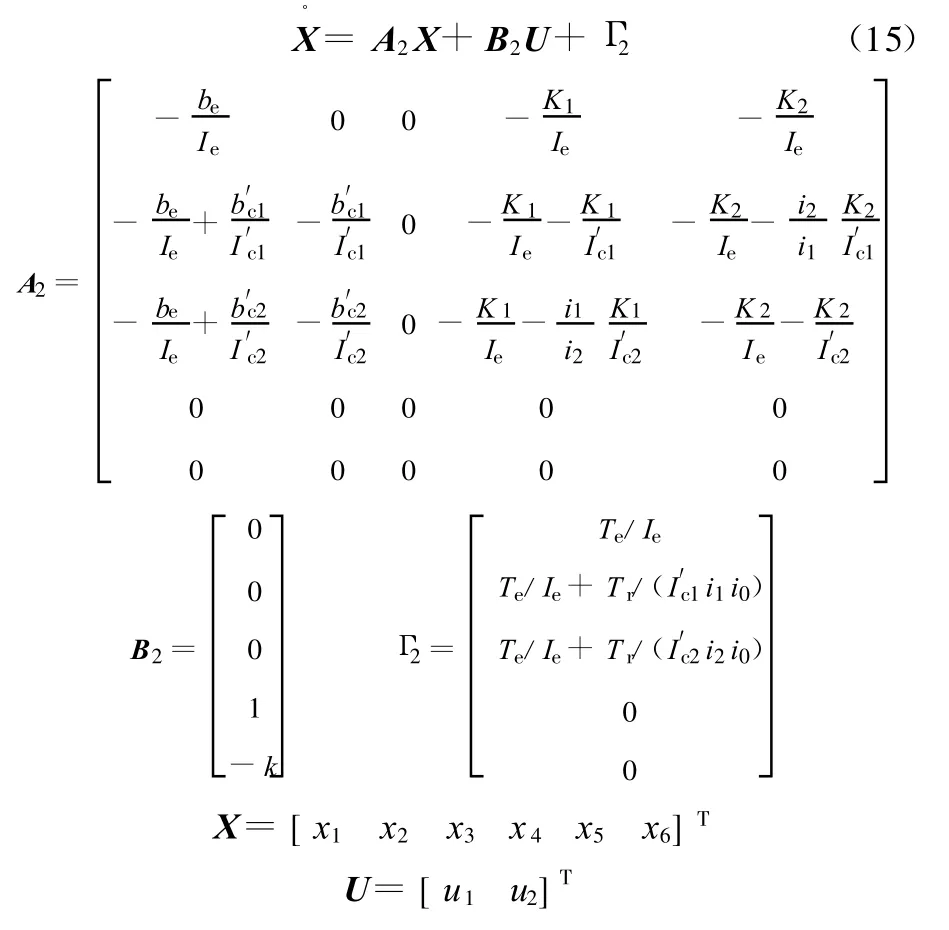
为了综合考虑滑摩功和冲击度的影响以及使x3(t f)=0,x4(t f)=0,选取

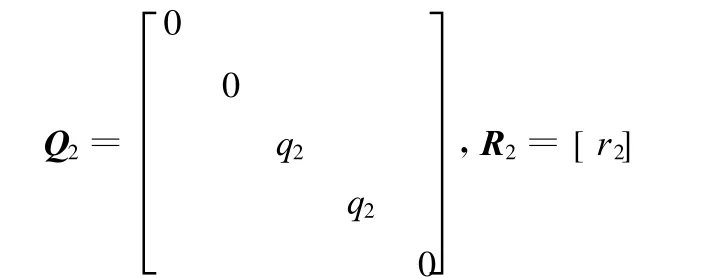
式中,q2、r2分别为所选取的加权系数。

则性能指标为

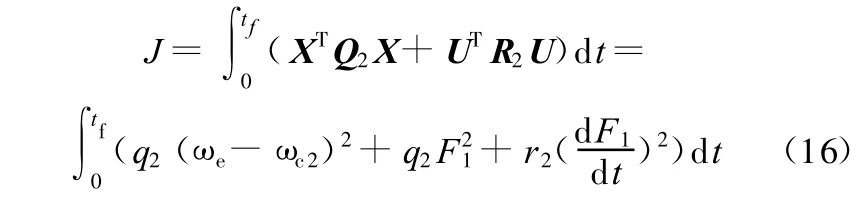
由于d F2/d t与d F1/d t,ωc1与 ωc2间存在比例关系,则目标泛函可视为对换挡过程中的滑摩功和冲击度的一个量度。

控制变量求法与起步控制相同,如式(13)、式(14)所示。值得说明的是,d F2/d t与d F1/d t间的关系在本文中为一设定值,其不同取值对系统状态会有不同的影响。

3 仿真结果及分析

3.1 DCT仿真模型

根据之前所建立的起步、换挡控制模型及DCT工作原理,在MATLAB/Simulink中建立DCT仿真模型(图3),其中,ωw为车轮角速度。

图3 DCT系统仿真模型示意图

仿真模型主要包括发动机模型、换挡控制模型、车辆模型以及在挡、换挡DCT变速器模型。车辆行驶过程中的发动机转矩通过节气门开度和发动机转速查表得到;换挡控制模块根据车速、当前挡位及节气门开度对照换挡规律给出换挡指令,而离合器的锁止信号则通过对离合器从动盘转速及离合器当前压力判定给出,即当 T cl＜T cmax、ωe=ωc时离合器由滑摩变为锁止,换挡结束;变速器模型分为换挡和在挡两个模式,通过换挡控制模块给出的信号判断某一运行模式,同时双离合器压力控制由变速器模型来实施,它根据当前车辆及变速器状态对离合器压力进行闭环控制;车辆模型则根据当前车速判定车辆运行状态,输出阻力矩。

3.2 仿真结果分析

设定模型控制参数,其中加权系数q1=3000,q2=500,r 1=r2=1,变比系数k=0.5,对起步和换挡工况进行仿真,结果见图4。由仿真结果可以看出：起步过程大约1s左右,较一般离合器起步要快,且发动机及离合器从动盘转速均平稳上升,状态稳定(图4a);起步过程中离合器1压力缓慢上升,达到最大值后有所下降(图4b);而换挡过程中,两离合器压力按照一定的比例增大或减小(图4c);双离合器按此压力曲线控制,使DCT在起步工况下,滑摩功为5k J左右,而换挡过程滑摩功仅为2k J左右,较一般换挡过程而言,滑摩功有效减小(图4d),且起步换挡过程中冲击度均不大于10m/s3,符合标准(图4e)。

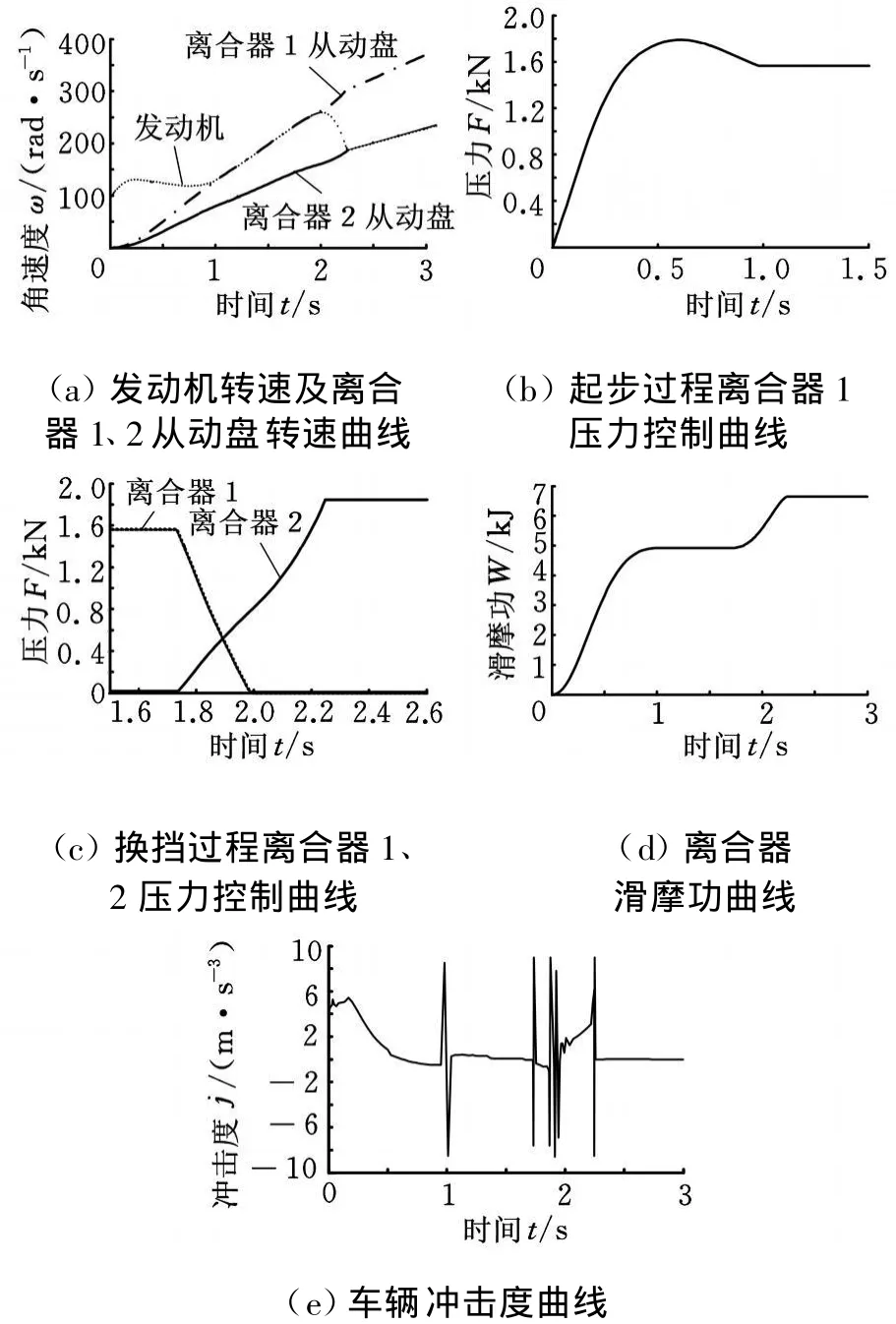
图4 起步、换挡过程性能曲线

3.3 加权系数的选取对控制效果的影响

根据之前分析可知,离合器的滑摩功和冲击度是两个互相矛盾的指标,而在二次型最优控制中,这两个指标的大小是由性能指标J中加权矩阵的系数q/r的取值所决定的：当q/r的值增大时,即滑摩功较多地决定了性能指标的大小,在性能指标最小化的过程中,滑摩功减小的程度较大,故最终滑摩功较小;反之,当q/r的值减小时,冲击度减小得较多。

对于二次型最优控制而言,加权矩阵值的确定是一个试凑的过程,如果选择不合理,也不能使系统状态达到最优。对于本文而言,如选取不恰当的q/r,不仅会导致黎卡提方程无法求解,起步、换挡过程无法完成等问题,还会导致起步换挡过程中的不稳定。现对以不同的q/r值进行仿真的结果作一分析说明。

由图5可以看出,仿真结果与之前的分析结果一致,q/r的值越大,起步和换挡时间均越短,起步过程中发动机转速与离合器转速的差值越大,滑摩功越小,冲击度越大;但当q2/r2=125时,虽然仍可以正常换挡,但冲击度曲线极不稳定(图5c)。而如果再减小q/r的值,则会导致换挡控制无法完成。

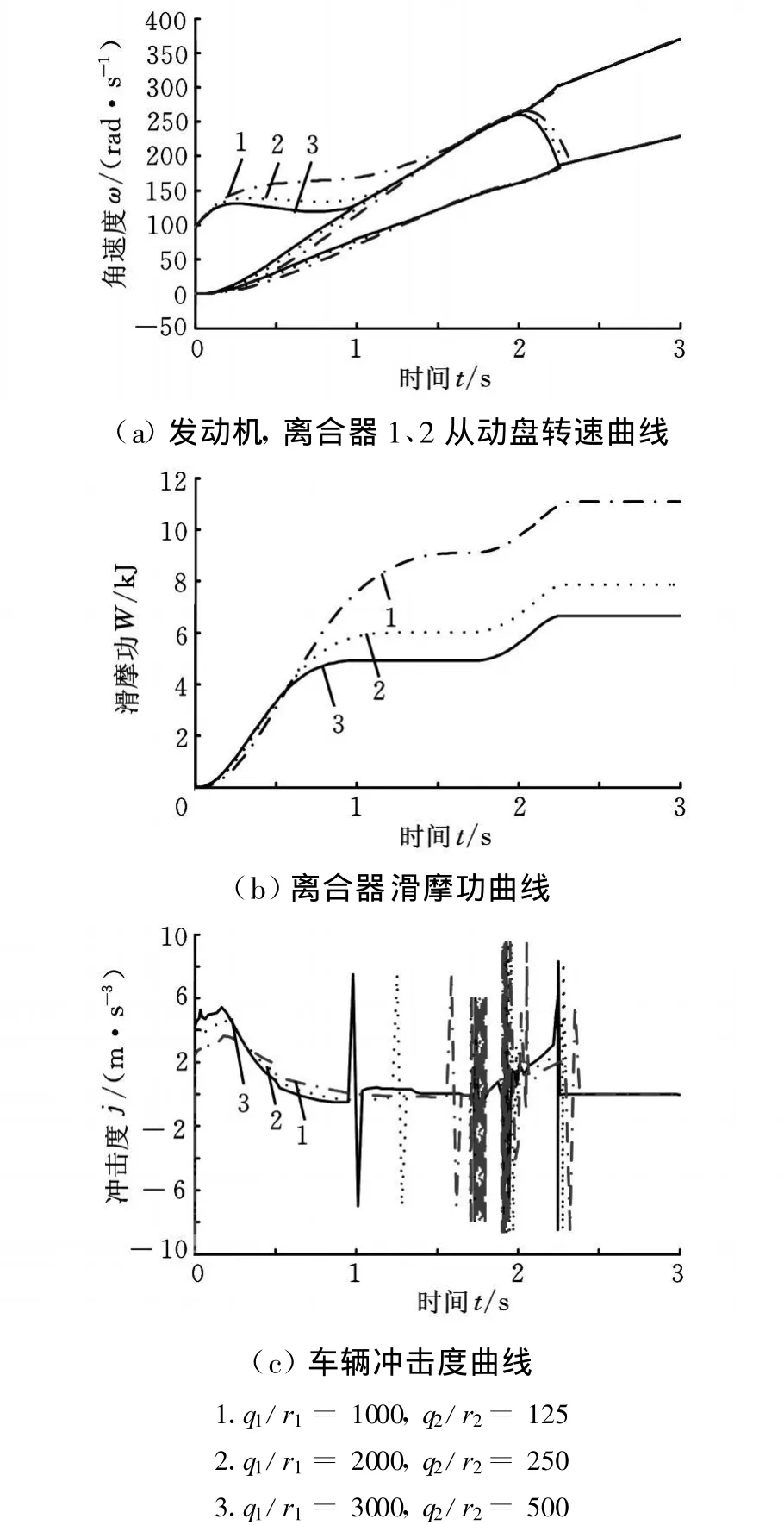
图5 不同权值系数下的起步、换挡性能曲线

3.4 变比系数的选取对控制效果的影响

根据2.3节的分析可知,为了有效求解换挡过程中两个离合器的压力,对其变化速率设定一定的变比系数,即 d F1/d t=-k d F2/d t。k值的大小对仿真结果有一定的影响,而对其值的选取只能采取经验试凑的方法。现设定k=0.1,0.2,…,0.9分别进行仿真,并对其结果进行分析。

根据图6所示的仿真结果,可得出以下结论：

(1)当k值减小时,离合器2完全接合的时间变长,从而导致换挡时间变长,滑摩功增大,冲击度减小。同时也可以看到,当k=0.8时,虽然换挡时间短,滑摩功小,但冲击度非常不稳定。

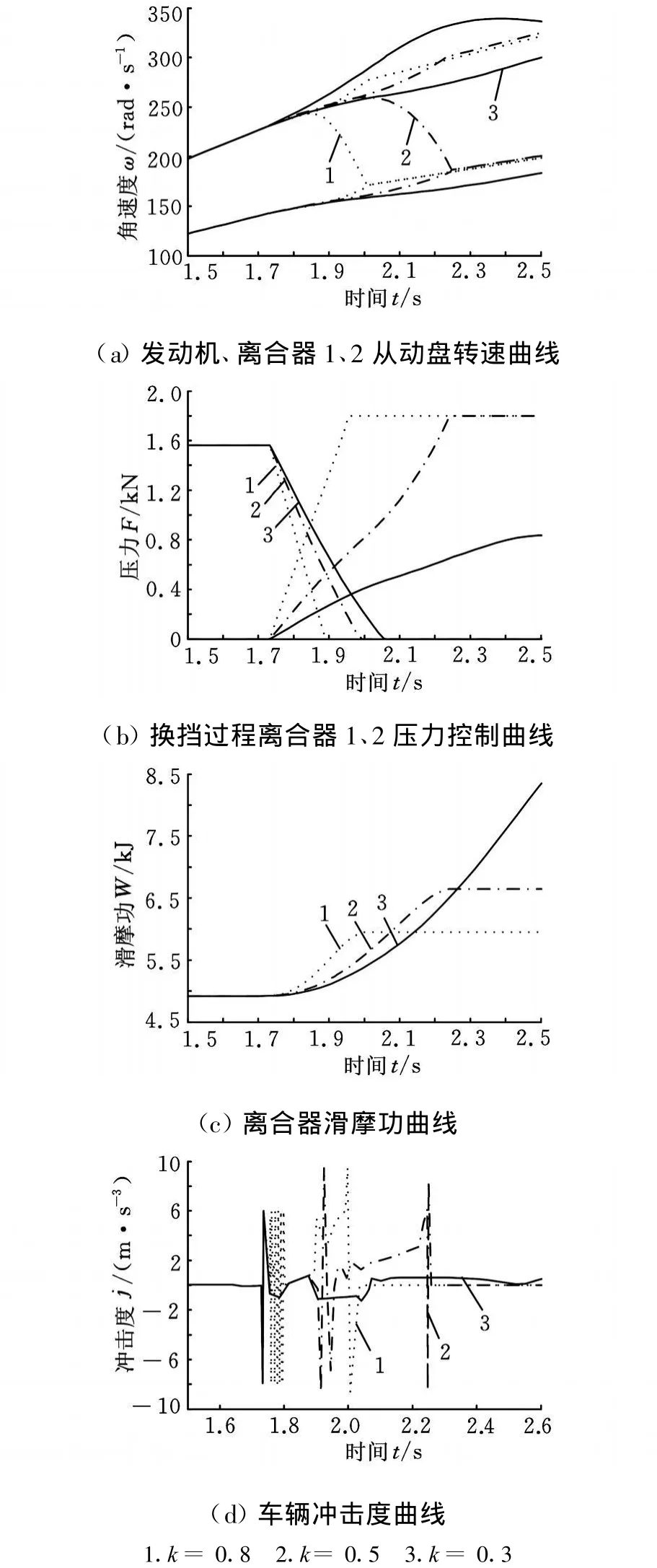
图6 不同变比系数下的换挡性能曲线

(2)当k=0.3时,由图6可知,换挡过程无法完成。这是由于变比系数过小,从而使得离合器2接合速度过慢造成的。

此外,如设定不恰当的k值会使二次型矩阵出现奇异值,从而无法继续求解获得最优控制压力,如 k=0.4,k=0.6,k=0.7 等 。

由此可以看出,k值的设定对系统最终的状态性能会有非常大的影响,而最优的两个离合器压力变化率的比值理论上是可求的,但基于文章整体考虑,本文仅针对不同的变比系数对仿真结果的影响作一讨论,不继续求解最优变比系数。

4 结论

(1)利用线性二次型最优控制的方法对DCT起步、换挡过程中的离合器压力进行了控制,控制方法简单,控制效果好。

(2)换挡过程中,最终的系统状态是由双离合器的输出转矩所决定的,而对于同一最优转矩,离合器1压力和离合器2压力的分配方式可以有许多种,设定两个离合器压力变比参数,可加快并最终确定各离合器的分配压力。同时,此压力变比系数的设定对系统的最终状态也会有较大的影响。

(3)控制参数的比值q/r决定了系统滑摩功和冲击度的大小,当q/r值较大时,滑摩功越小,冲击度越大,换挡时间越短。而对其值的合理确定只能基于经验通过试凑完成,如该值确定得不恰当,会导致无法完成换挡或是系统不稳定等情况。

离合器压力的变比系数在理论上可求得其最优值。进一步的研究将通过对此变比系数的优化以对本文控制方法进行改进,试图将换挡过程中离合器压力的变比系数作为优化变量,进行实时调整,以获得更优的压力曲线。

[1] Kulkarni M,Shim T,Zhang Yi.Shif t Dynamics and Control of Dual-clutch Transmissions[J].Mechanism and Machine Thoery,2007,42：168-182.

[2] 牛铭奎,程秀生,高炳钊,等.双离合器式自动变速器换挡特性研究[J].汽车工程,2005,26(4)：453-457.

[3] 胡宏伟.湿式自动离合器接合过程特性的研究[D].杭州：浙江大学,2008.

[4] 葛安林.车辆自动变速理论与设计[M].北京：机械工业出版社,1993.

[5] 张洪钺,王青.最优控制理论与应用[M].北京：高等教育出版社,2006.

[6] Glielmo L,Vasca F.Optimal Control of Dry Clutch Engagement[C]//SAE World Congress,2000.Transmission and Driveline Symposium 2000.Detroit：SAE,2000-01-0837,2000.