高斯模糊图像的复原处理与研究

(长江大学电子信息学院，湖北 荆州 434023)

张春海

(辽河油田裕隆实业集团检波器厂，辽宁 盘锦 124010)

在图像的形成、传输、存贮、记录和显示过程中，光学系统的像差、成像系统的非线性、大气扰动、运动、散焦和系统噪声等因素都会造成图像模糊和变形[1]。因此，要得到高质量的数字图像，需要对图像进行复原，使其与原图像尽可能逼近。但大多数情况下退化过程是不可知的，在图像模糊的同时，噪声和干扰也会同时存在，这为复原过程带来了困难。经典图像复原在图像处理中占有重要的地位，其复原的前提条件是需要知道点扩展函数和噪声分布，其中一些算法被广泛使用[2]，但如何对其进行改进，使之适合不同的复原情况，是一个值得研究的课题。笔者在对经典图像复原算法分析的基础上，针对高斯模糊图像，对3种经典图像复原算法进行了仿真实验，为不同应用场合及不同图像数据条件下选择相应的复原算法以及系统参数提供了一定的依据。

1 图像退化模型

在获取数字图像过程中经常发生图像质量下降或者退化，由于导致图像退化的原因很多，所以通常用统一的数学模型对图像的退化过程进行描述。如果一幅原始图像f(x，y)在1个退化函数和1个加性噪声项的作用下生成观测图像g(x，y)，退化函数可以认为是线性、位置不变的，且噪声也与位置和当前像素值无关，则退化过程可以被模型化为[3,4]：

g(x,y)=f(x,y)*h(x,y)+n(x,y)

(1)

式中，h(x，y)表示退化函数的空间描述，也称为点扩散函数(Point Spread Function，PSF)；*表示空间卷积，n(x，y)为加性噪声。可以用向量矩阵的形式将式(1)的退化模型表示为[4]：

g=Hf+n

(2)

式中，g是观测图像；f是原始图像；n是噪声，假设g(x，y)的大小是N×N，则可以用g(x，y)的第1行的图像元素形成向量g的前N个元素,用第2行的图像元素形成向量g的下N个元素，依次类推,最终的向量维数为N2×1。因为这些向量是用同样的方法构建的,所以g、f和n尺寸相同，都是N2×1的列向量，因而H是N2×N2的PSF参数矩阵。从模型中估计f的问题称为线性反转问题，其是经典图像复原研究的基础[2]。

2 逆滤波复原技术

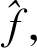
(3)

(4)

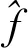
(5)

根据循环矩阵对角化的讨论，式(5)可以写成如下形式的估计：

(6)

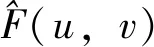
(7)

由式(7)可知，如果H(u,v)在uv平面上取零或很小，会带来计算上的困难。另一方面，噪声还会带来更严重的问题，若加入噪声则得到：

(8)

由式(8)可以看出，如果H(u,v)在uv平面上取零或很小，N(u,v)/H(u,v)就会使恢复结果与预期结果有很大差距。实际上H(u,v)随u,v与原点距离的增加而迅速减小，而噪声N(u,v)一般变化却缓慢。在此情况下，恢复只能在与原点较近(接近频域中心)的范围内进行，所以一般情况下逆滤波器并不正好是1/H(u,v)，而是u和v的某个函数，可记为M(u,v),常被称为恢复转移函数。一种改进方法是取M(u,v)为：

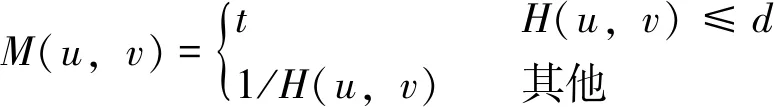
(9)

其中，t和d均为小于1的常数，而且d选得较小为好。

3 维纳滤波复原技术

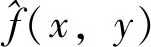
(10)

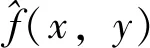
(11)

与解式(4)相同，可得有约束恢复公式(令s=1/a):

(12)

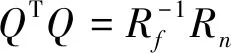
(13)

式中，H(u,v)表示图像的退化函数；Sn(u,v)/Sf(u,v)称为噪信功率比；|H(u,v)|2=H*(u,v)H(u,v)，H*(u,v)表示H(u,v)的复共轭；Sn(u,v)=|N(u,v)|2表示噪声的功率谱；Sf(u,v)=|F(u,v)|2表示未退化图像的功率谱。

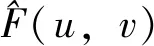
(14)

由此可以看到，当K为0时，维纳滤波器就转化为标准的逆滤波器，而逆滤波器是从退化模型严格反推出来的，所以当K不等于0时，虽然能抑制噪声的扩大，但复原的模型没有去卷积滤波器精确，容易造成复原的失真。K越大，抑制噪声效果越好，但复原不准确，图像会比较模糊；K越小，复原越准确，然而噪声抑制效果不好。

4 有约束的最小二乘方滤波复原技术

约束最小二乘方滤波式从式(12)出发来确定变换矩阵Q。为了减小振荡，可以建立基于平滑测度的最优准则[4]，例如，可使某些二阶微分的函数最小化，f(x,y)在(x,y)处的二阶微分可用下式近似：

(15)

上述二阶微分可以用f(x,y)与下列算子卷积得到：

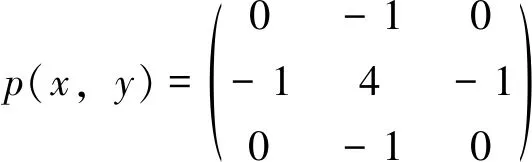
基于这种二阶微分的最优准则是：

该函数的约束条件为：

(16)

其最优化问题的频域解决办法由下式给出：

(17)

其中，s是一个必须加以调整的参量，以便约束条件得到满足;P(u,v)是函数p(x,y)的傅立叶变换。

5 试验结果及分析

图1 噪声方差为2时3种算法的复原结果

根据上述复原算法原理，笔者利用matlab编程实现了3种图像的复原算法。图1是对高斯模糊并有加性噪声方差为2的退化图像利用3种算法复原的结果。图1(a)是分辨率为328×180的8位BMP原始灰度图；图1(b)是计算机模拟出的高斯模糊并有加性噪声影响的退化图像，模糊函数是均值为0、均方差为6、滤波尺寸为7的高斯函数，添加的高斯噪声均值为0，方差为2；图1(c)是逆滤波复原图像，式(9)中t取0.9，d取0.07；图1(d)是维纳滤波复原图像，式(14)中K取0.005；图1(e)是有约束的最小二乘滤波复原图像，式(17)中s取10-3。可以看出，逆滤波和有约束的最小二乘方技术抑制噪声的能力虽然不如维纳滤波，但由于噪声方差较小，因而3种方法复原的结果区别不大，细节保持能力均较好。

图2 噪声方差为20时3种算法的复原结果

图2是对高斯模糊并有加性噪声方差为20的退化图像利用3种算法复原的结果。图2(a)是在图1(b)的基础上将高斯噪声方差增加到20的退化图像；图2(b)是逆滤波复原的图像，式(9)中t取0.07，d取0.13；图2(c)是维纳滤波复原图像，式(14)中K取0.021；图2(d)是有约束的最小二乘滤波复原图像，式(17)中s取10-2.1。可以看出，在加大噪声方差的情况下，逆滤波和有约束的最小二乘方复原图像受噪声的影响较明显，图像中噪声颗粒偏大，维纳滤波复原技术抑制噪声能力要好于其他2种方法，但其模糊程度较大，而有约束的最小二乘方复原技术的细节保持能力最强。

图像复原质量既可以从主观上评价，也可以从客观上定量描述，常用的图像复原客观评价标准是均方误差MSE[6](Mean Square Error)。假设f(x,y)的尺寸为M×N，MSE可用下式计算：

(18)

表1 3种方法对不同噪声的退化图像复原结果的MSE

表1列出了3种复原算法对不同退化图像复原结果的MSE，各个参数的取值为文中所述的数值。图像的MSE越小，说明复原之后的图像与原始图像越接近，复原效果越好。从表中数据可以看出，在噪声方差较小时，3种方法的MSE均较小且相差不大，当噪声方差为20时，3种方法的MSE也随着变大，有约束的最小二乘方复原的均方误差最小，因而其复原效果最好。

6 结 语

通过对上述3种算法的研究并对计算机模拟出的高斯模糊并有不同加性噪声影响的2幅退化图像进行复原处理，在寻找较好视觉效果上取得了丰富的经验数据。从复原图像质量以及客观评价标准来看，在噪声方差较小时，3种方法的复原效果均较好；在加大噪声方差时，维纳滤波复原技术抑制噪声的能力最好，有约束的最小二乘方复原技术的细节保持能力最强。所以在高噪声环境下，可以选择有约束的最小二乘方复原技术来达到更好的视觉效果。当然，在实际应用中，要根据经验来选择最佳参数进行图像复原。对于今后图像复原算法的研究，应以提高复原算法的有效性和效率为主要研究方向，不断提高复原图像的质量和速度，并降低算法的复杂度。

[1]明文华.运动模糊图像复原算法研究[D].合肥：安徽大学，2004.

[2] 杨彦.图像复原算法研究[D].成都：四川大学，2004.

[3] 钟金辉，彭荫荣，王万迎，等.基于 Lucy 算法的散焦图像复原[J].微计算机信息，2009，25(5)：279～280.

[4] Rafael C，Richard E.数字图像处理[M].阮秋琦译.北京：电子工业出版社，2007.

[5]何蕾.数字图像复原算法研究[D].合肥：合肥工业大学，2007.

[6]蒋伟，胡学刚.一种基于偏微分方程的图像复原新模型[J].计算机工程与应用，2008，44(14)：187～189.