蛋白质空间结构数字特性统计分析及应用
2010-05-29章社生
章社生,何 康,范 宁,晏 臻,王 星
(武汉理工大学理学院统计学系, 湖北 武汉 430070)
0 引 言
蛋白质是构成生命的物质基础,它是与各种形式的生命活动紧密联系在一起的物质.在催化生命体内各种反应进行、调节代谢、抵御外来物质入侵及控制遗传信息等方面都起着至关重要的作用,是生命科学中极为重要的研究对象.蛋白质是由一条或多条多肽链组成的生物大分子,每一条多肽链有数十到数百个氨基酸残基不等;各种氨基酸残基按一定的空间顺序排列.不同的蛋白质空间结构有不同的生命功能.揭示蛋白质的生命活动规律,研究蛋白质的折叠,设计具有特定功能的蛋白质,都需要了解蛋白质空间结构.文献[1]介绍了X射线晶体学、二维核磁共振(2D-NMR)和低温冷冻电镜等蛋白质空间结构的实验测定方法.应用这些方法,实验室已测定大量蛋白质空间结构,并以PDB文件形式贮存在公共数据库中,免费供世界各地研究者使用.文献[2]应用统计分析方法,利用数据挖掘中的数据分布拟合理论对生物科学领域中的蛋白质侧链空间结构进行统计分析.以世界上广泛使用的生物分子三维结构数据库PDB为基础,利用多氨酸残基侧链碳原子间距离的统计分析方法,通过正交试验设计和信息论中的熵函数等相关知识,给出了不同位置、不同氨基酸残基种类对侧链结构的影响. 文献[3-4]用统计和几何方法给出了氨基酸在蛋白质空间结构中的深度计算,并利用PDB数据库得到了不同氨基酸在蛋白质中的深度倾向性因子,并得到了这些倾向性因子与氨基酸的物理、化学综合特性的相关性质.根据蛋白质空间结构和蛋白质生物性质,国内外学者建立了多种蛋白质折叠模型和蛋白质设计模型[5-9];这些模型一般应用能量函数进行计算,利用蛋白质空间结构的数值特征是构造能量函数的一种途径.
本文根据PDB数据文件计算蛋白质空间结构的数值特征,构造数值特征的能量函数.PDB收集的蛋白质数据来源于X光晶体衍射和核磁共振的数据,经过整理和确认后存档而成.蛋白质种类众多,分类方式各异.按分子形状分类,可分为球状蛋白质和纤维状蛋白质.鉴于大多数蛋白质属于球状蛋白质,如血红蛋白、肌红蛋白、酶、抗体等[10-11],本文主要选取了球蛋白作为研究对象,并将其分为五大类,即血红蛋白、肌蛋白、激素、抗体、生物膜的成分,分别抽样进行计算与分析.文中叙述数字特征的计算原理及血红蛋白等五类蛋白质的数字特征,讨论氨基酸的数字特征,给出了数值特征能量函数的构造原理.
1 蛋白质数字特征
本文只讨论每一个蛋白质PDB文件中关于原子(ATOM)部分的数据.
1.1 数据处理方法
从数据库中查询选取出属于肌蛋白、血蛋白、激素、抗体、生物膜共五类的部分蛋白质,并按类别存放(每类选取60~100个蛋白质),然后按下面步骤计算数字特征.
a.对于第i个蛋白质分子,提取出PDB文件中所有ATOM的立体坐标数据,其中(xij,yij,zij)为第j个原子的立体坐标.
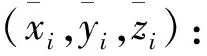
c.计算该蛋白质分子第j个原子到中心点距离rij的期望与标准差.该蛋白质分子内原子到形心距离的数学期望与标准差分别为:
d.计算该类蛋白质分子的数学期望与标准差的均值:
其中m表示所考察的该类蛋白质的蛋白质分子个数.
e.统计每类蛋白质各分子的数学期望和方差(标准差),分析每类蛋白质数字特征的概率分布情况.
1.2 数据结果分析
1.2.1 血红蛋白 血红蛋白原子到形心距离的数学期望约为22.69,平均标准差约为7.30.对属于血红蛋白,所考察的蛋白质分子的距离数学期望在9.785到48.115之间,标准差在2.748到16.324之间,约40%的蛋白质分子数学期望在10到20范围之间,43%的分子落在20到30 区域内.然而80%标准差在3到10内,且大多集中在5左右.因此推测,属于血红蛋白的蛋白质分子,其原子到分子形心距离的数学期望集中分布在15~30之间,分子的结构较为密集、聚中.
1.2.2 肌蛋白 肌蛋白原子到形心距离的数学期望约为22.85,平均标准差为8.25.所考察的属于该类蛋白的蛋白质分子的距离数学期望在10.989到104.242之间,标准差在3.918至58.768之间,两者的极差均较大.观察距离数学期望和标准差的,大约80%的肌蛋白分子的原子到中心距离在10到30之间,标准差在4到10之间.总体上看,分布仍然比较集中,波动不大,但有几种肌蛋白分子偏离均值较远,分子内部原子到形心的平均距离可达到100左右.
1.2.3 抗体 抗体原子到形心距离的数学期望约为25.98,平均标准差为8.89.所考察的抗体蛋白质分子的距离数学期望分布于3.036到51.928,标准差在1.500到19.842,约80%的抗体的距离数学期望在20到40之间,整体上没有很大的波动.
1.2.4 激素 激素原子到形心距离的数学期望约为18.13,平均标准差6.57,对属于该类的蛋白质分子来说,距离数学期望仍集中在10到30,标准差较均匀地分布在2到10之间.激素分子相对其他几类蛋白质较小,原子的分布也相对集中.
1.2.5 生物膜的成分 生物膜原子到形心距离的数学期望约为20.45,平均标准差为6.57,该类分子的原子到形心距离的数学期望在10到20附近较多,也有分子在60附近,分布体现的规律性不强,这可能是由于样本数量不足所导致,也可能是生物界中自身的差异多所致.通过上述不同类蛋白质的数据分析,如表1所示,激素蛋白的整体数学期望最小,且方差也是较小;其后依次是生物膜成分、血红蛋白、 肌蛋白、抗体.在这五类蛋白质中,原子到其形心的平均距离较大者,这种距离的平均偏差一般也较大.
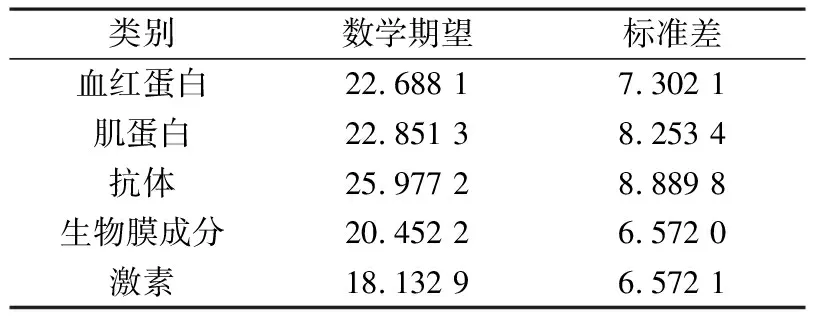
表1 五类蛋白质的数字特征对比表
2 氨基酸的数字特征
进一步研究蛋白质分子的数字特征,考虑蛋白质的组成成分氨基酸.基于氨基酸的种类众多,只考虑20种天然的氨基酸.PDB文件中氨基酸以残基序列进行记录,为此笔者研究各类蛋白质中属于同一种残基的原子的数字特征,进而进行定性与定量分析.
2.1 数据处理方法
计算各类蛋白质分子中原子到相应分子中心的距离rij,将所有考察的原子的距离依据各原子的残基名分类,统计各类(残基)中原子到形心距离的数学期望(平均值)与标准差.
2.2 数据结果分析
对于血红蛋白,不同残基下的数学期望差异较小,大致都在28左右波动;并且离散程度也无明显的差异.因此笔者认为残基的不同对原子到形心距离的影响相对弱.另外,在组成血红蛋白的原子中,残基MET出现次数最少,而LEU、LYS较多.对于肌蛋白,数学期望差异仍是不显著,大体在35到40之间;相对的标准差差异较小,这跟血红蛋白的情况类似.在蛋白质的组成中,残基GLU、LEU、LYS出现较多,TRP、CYS较少.类似地,对激素、抗体、生物膜成分三类蛋白,同类蛋白数学期望和标准差的分布都较为集中,没有大的波动.可以推断,对于同种蛋白质,残基对其原子到相应蛋白质分子中心距离的影响不大.对于激素,残基LEU贡献显著,CYS、TRP出现频率较小;抗体中具有残基SER、LEU的原子较多,具有残基MET、CYS的较少;对于生物膜的成分,LEU、ARG最多,CYS最小.
此外,笔者研究对于同一种残基,不同类的蛋白中数字特征及原子个数的差异问题.残基ALA和CYS对应的数字特征如表2所示,由表可知,对于残基ALA,在血蛋白、肌蛋白、抗体和生物膜成分中出现的频率高于激素.对于残基CYS,肌蛋白出现的频率远高于激素.另外,在不同类型的蛋白质中,其氨基酸的数字特征各不相同.
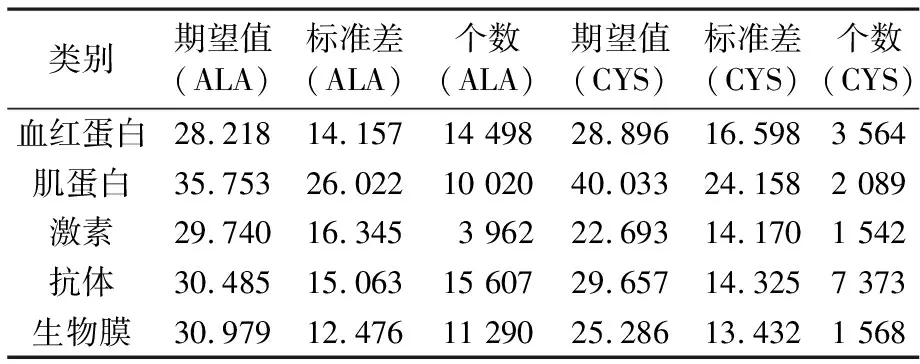
表2 五类蛋白不同残基的对比表
一般的,各类蛋白中残基LEU出现最为频繁,CYS较小.对于同种蛋白质,残基对其原子到相应蛋白质分子中心距离的影响不大.另外,笔者研究各残基中原子到形心距离的分布情况,发现频数随着距离的增大而递减.基于以上的数据分析,从侧面证实了不同类型的蛋白质的特征差异性与一致性.同时也说明了不同的蛋白质的组成不同,对应的数字特征也不同.这也许可以从另一个角度提供组合蛋白质的思路.
3 数字特征能量函数
设Eij为第i种蛋白质的第j种残基(i=1~5, 1~20)的期望,Pij为第i种蛋白质的第j种残基期望的发生概率,定义为:
式中Pi为第i种蛋白质发生的概率,pij为第i种蛋白质第j种残基在第i种蛋白质发生的条件下的条件概率.Ei.为第i种蛋白质的期望, 它为Eij对所有的j求和. 定义期望能量函数如下:
这里P0为Pij的概率平均值.上式建立了能量函数与蛋白质种类和残基种类之间的关系,它可以用于蛋白质设计.根据上面五类蛋白不同残基的对比表给出的残基ALA和CYS的预期,笔者容易求出概率pij, 其结果列于表3. 由表可知, 肌蛋白中残基CYS的期望概率最大,激素中残基CYS的期望概率最小.相对残基ALA的期望概率,CYS的期望概率比较分散.文献[7]认为比较分散概率有助于蛋白质设计.
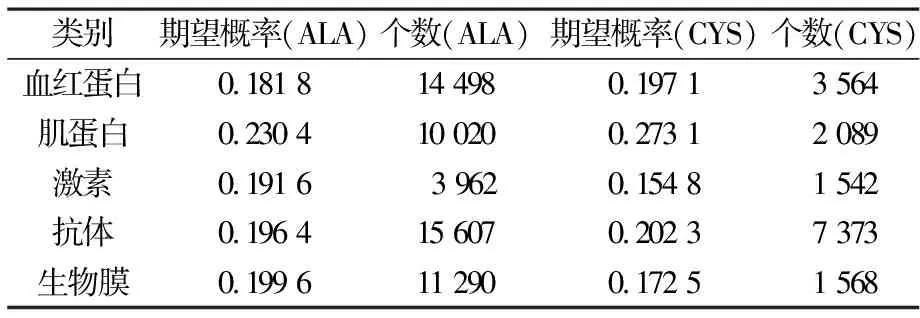
表3 五类蛋白不同残基的期望概率
4 结 语
本文对蛋白质分子的结构特性进行了量化处理,利用统计分析,数据挖掘知识,从蛋白质的数字特征入手,讨论五类蛋白质的特点,进而根据20种残基分组深入研究,从不同角度分析得出了一系列的结论,为蛋白质的结构数学化提供了思路,也为组合氨基酸生成蛋白质提供了数据支持.
在数学上,数字特征的计算原理是非常成熟的.但在生物中,有许多生物数字特征计算工作没有完成.蛋白质是研究得较多的生物对象,但笔者查阅了国内外文献资料,没有发现完整研究蛋白质数字特征计算的文章.至今为止,人们已测量的蛋白质数据是海量的,通过数字特征计算是揭示蛋白质空间结构生物性质的途径之一.用数字特征构造能量函数是生物数据二次挖掘,该能量函数能用于蛋白质设计.另外,本文工作还有极大的拓展空间,例如,有更多种类蛋白质的数字特征需要计算,DNA、RNA等生物基团的数字特征也需要计算和分析.
参考文献:
[1]江凡.蛋白质空间结构的实验技术和理论方法[J].物理,2007,36(4):272-279.
[2]王昕,毛炳蔚,王福伟,等.蛋白质空间结构的统计分析[J].山西大同大学学报:自然科学版,2008,24(5):3-8.
[3]沈世镒,胡刚,张华.氨基酸在蛋白质空间结构中的深度倾向性因子[J].生物数学学报,2007(7):305-310.
[4]沈世镒,胡刚,张华.蛋白质空间形态特征分析与计算方法[J].工程数学学报,2006,22(2):225-234.
[5]胡敏,彭群生.一种基于空间密度特征的蛋白质结构相似性判定方法[J].工程图学学报,2005,26(1):90-95.
[6]王仲君,王能超,毛黎明.基于自回避搜索遗传算法的蛋白质折叠研究[J].武汉理工大学学报,2005,27(8):91-95.
[7]Faraggi E,Yang Y, Zhang S,et al. Predicting continuous local structure and the effect of its substitution for secondary structure in fragment-free protein structure prediction[J].Structure,2009,17:1515-1527.
[8]Liang S, Wang G, Zhou Y. Refining near-native protein-protein docking decoys by local re-sampling and energy minimization[J]. Proteins,2009,76:309-316.
[9]Xue B, Faraggi E, Zhou Y. Predicting residue-residue contact maps by a two-layer, integrated neural-network method[J].Proteins,2009,76:176-183.
[10]张佑红,陈龙,靖志强,等.不同周期Sf9细胞琥珀酸脱氢酶酶活的研究 [J].武汉工程大学学报,2009,30(5):4-6.
[11]奚强,李俊,林丫丫,等. L-核糖的合成[J].武汉工程大学学报,2009,30(5):18-20.
