离散系统教学中MATLAB的应用*

曹建云 王娟 朱建伟

南通大学电气工程学院 江苏 南通 226019

离散系统教学主要涉及采样控制系统的采样、复现过程及其数学基础、采样控制系统的性能分析等。采样时间系统与连续时间系统的数学分析工具在稳定性、动态特性、静态特性等方面都具有一定的联系和区别。最根本的区别就是，前者的系统中至少有一个以上在时间上是离散的信号，因此这种系统要用离散数学模型如脉冲传递函数去描述。由于Z变换只能反映在采样时刻的信息，因此用这种方法去分析系统，只有当采样周期T很小时，才能使c*(t)与c(t)基本相一致。香农采样定理给出不失真地复现连续信号的最低采样频率要求。在这里分别就MATLAB函数和Simulink模块在离散系统教学中的应用进行讨论。

1 应用MATLAB函数对采样系统进行分析

MATLAB中提供大量函数，可以对采样系统进行分析。应用dstep、dimpulse可以分别绘制出采样系统的单位阶跃响应和单位脉冲响应曲线，而应用dbode、dnyquist可以分别绘制出采样系统的伯德图和奈氏曲线。

1.1 用dstep绘制离散系统单位阶跃响应曲线

[c,t]＝dstep(n,d)

[c,t]＝dstep(n,d,m说明：dstep函数可以绘制多项式函数g(z)＝n(z)/d(z)表示的系统的阶跃响应曲线；dstep(n,d,m)函数可绘制出用户指定的采样点数为m的系统的阶跃响应曲线；当带有输出变量引用函数时，可得到系统阶跃响应的输出数据，而不直接绘制出曲线。

图1 系统结构图

1.2 用dimpulse绘制离散系统单位脉冲响应曲线

调用格式和说明均类似于dstep。

【例】画出如图1所示系统的单位阶跃相应曲线。

n＝[2.5280]，d＝[11.160.368]，dstep(n,d,100)，所得响应曲线如图2所示。利用图中相关工具直接可以从图中读得系统超调量、峰值时间和调节时间等动态性能指标。

2 用Simulink模块对采样系统进行建模分析

图2 例题系统阶跃响应曲线

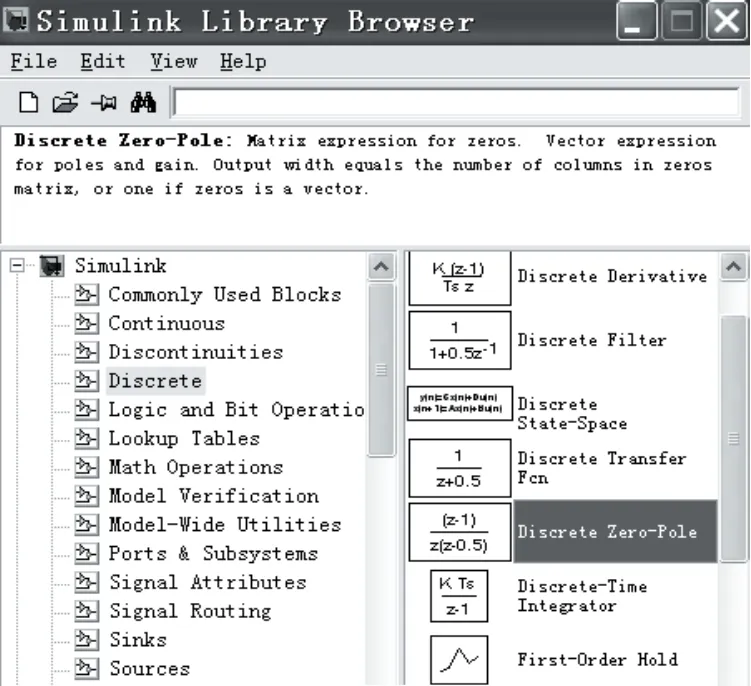
图3 利用Simulink建模

图4 利用Simulink中Discrete Zero-Pole对话框

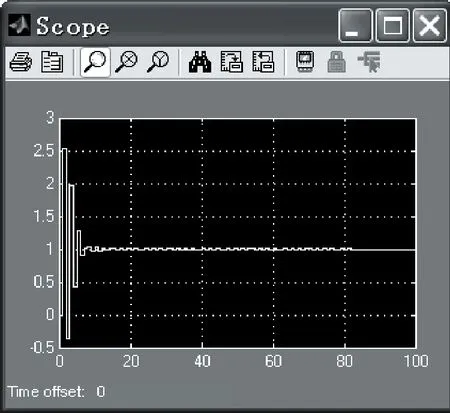
图5 例题Simulink仿真结果

MATLAB中Simulink提供现成的脉冲传递函数模块，只要对相关参数进行修改就可以得到对应的离散系统数学模型。如上例所述系统，其开环模型如式①所示，除了利用MATLAB函数对其进行建模分析，还可以应用Simulink模块对采样系统进行建模仿真。如图3所示，拖动Discrete Zero-Pole模块，参数修改如图4，对其进行仿真，则得到如图5所表示的仿真结果。对比图2，可以发现采用两种方法的仿真结果是一致的。

3 离散系统稳定性分析

线性离散系统稳定的充分和必要条件是：闭环脉冲传递函数所有极点均落在z平面的单位圆内。因此可使用roots命令求解系统闭环极点，如果所有极点均落在z平面的单位圆内则系统稳定。

Roots命令调用格式：r＝roots(p)。说明：p为系统模型特征多项式。如例题式②表示的系统闭环特征多项式p＝[11.160.386]，调用roots(p)命令，则有：

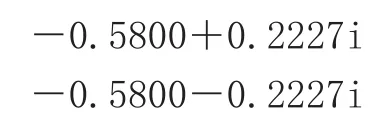
可以看出两个极点均落在z平面的单位圆内，所以系统稳定。

4 结论

离散时间系统是信号与系统课程的重要章节，涉及的数学运算较为繁复。在离散时间系统分析的课堂教学中，借助科学计算软件MATLAB能在阐述概念的同时，避免过多的手动运算，即时给出相关结果和函数图形，可以在有限的时间内展现整个系统分析的流程，节省时间，改善授课效果。利用MATLAB快速方便的运算及绘图功能，可以直观地表达系统分析理论在实践中的应用，达到很好的教学效果。

[1]赵冬梅.MATLAB在控制技术课程教学中的应用[J].中国科技信息,2009(09)

[2]张正文,钟东.基于MATLAB的离散时间系统分析[J].咸宁学院学报,2007(06)

[3]苏博妮,化希耀.基于MATLAB的离散时间系统Z域分析[J].塔里木大学学报,2009(01)