MATLAB在小波理论学习中的应用

王鑫

江南大学物联网工程学院 江苏 无锡 214122

1 引言

小波工具箱使用图形化工具和命令行函数扩展MATLAB技术的计算环境，可以用于开发基于小波的算法，进行信号和图像的分析、综合、去噪和压缩等运算[1]。

小波工具箱支持对小波属性和小波应用的交互式研究。这对于语音和音频处理、图像和视频处理、生物成像以及通信和地球物理学中的一维和二维应用是非常有益的[2]。

通过对小波工具箱的目录结构和源代码的深入分析，研究小波工具箱的体系结构和实现技术。这样的实践有助于学生对小波理论的深入理解。

2 小波滤波器的计算

从小波理论可以知道，如果尺度函数φ是紧支的，那么对应的尺度滤波器W的长度是有限的，就可以被看做一个FIR滤波器[3]。小波工具箱将这个FIR滤波器保存为系统预定义的数据文件。载入这个数据文件，即可获得尺度滤波器W。从尺度滤波器W出发，定义4个FIR滤波器，如表1所示。

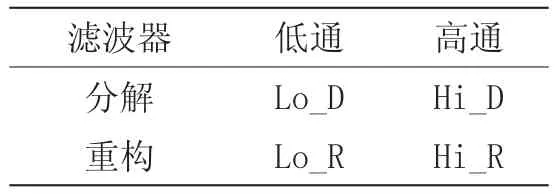
表1 分解滤波器和重构滤波器

从计算小波滤波器的wfilters函数的源代码可知，上述4个滤波器的计算方案如图1所示。首先，对W进行归一化，即可求得Lo_R。从Lo_R出发，使用qmf函数和wrev函数，即可求得Hi_R、Lo_D和Hi_D。其中，qmf函数使得Hi_R和Lo_R是正交镜像滤波器，wrev的作用是翻转Hi_R和Lo_R的系数。因此，Hi_D和Lo_D也是正交镜像滤波器。

在完成小波函数ψ(t)、尺度函数φ(t)或者小波滤波器的定义的基础上，即可进行各种小波分析的任务：连续小波分析、离散小波分析和小波包分析。

3 离散小波分析

将小波理论应用于实际的工程问题中，使用较多的是离散小波变换。在小波工具箱中，离散小波变换的分析-分解函数主要有dwt函数（单级离散小波变换）和wavedec函数（多级小波分解），重构-综合函数主要有idwt函数（单级逆离散小波变换）、waverec函数（多级小波重构）和wrcoef函数（从小波系数重构单个分解分支）。这些函数之间的计算关系如图2和图3所示。

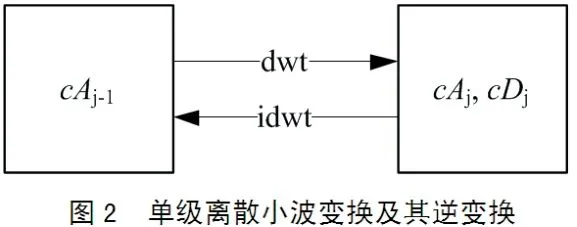
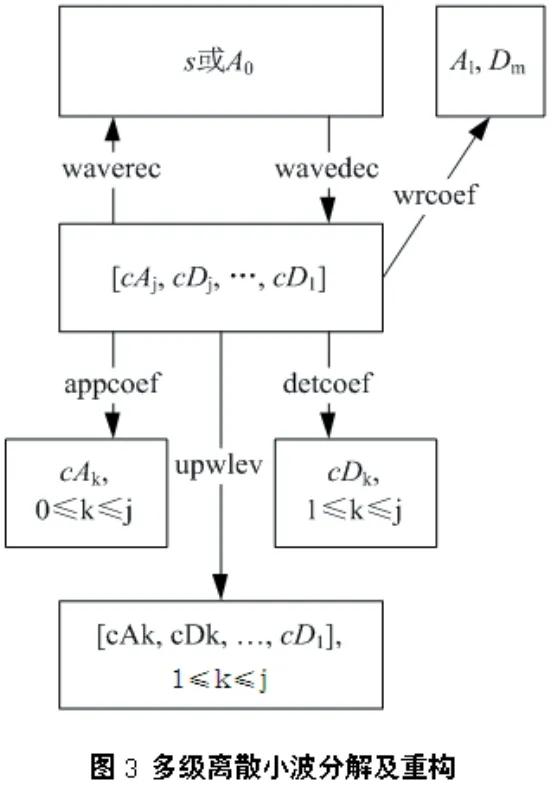
图2和图3中，s为原始信号；Ak（0≤k≤j）为第k级逼近；Dk（1≤k≤j）为第k级细节；cAk（1≤k≤j）为第k级逼近系数，cDk（1≤k≤j）为第k级细节系数，[cAj,cDj,…,cD1]为第j级小波分解，j≤1。

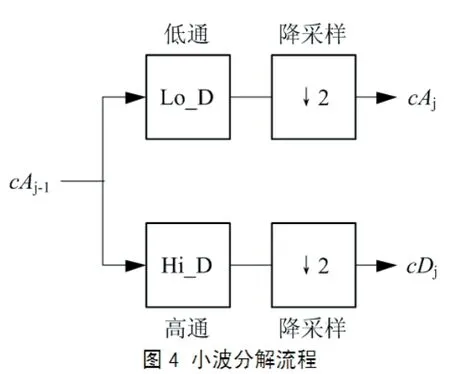
从源代码可以得出，wavedec函数是通过递归地执行dwt函数来实现的。具体来说：第一步，从信号s开始，分别与用于逼近的低通分解滤波器Lo_D和用于细节的高通分解滤波器Hi_D进行卷积运算，然后分别进行二进采样（降采样）来获得逼近系数cA1和细节系数cD1。下一步，使用相同的方案对逼近系数cA1进行分割，即用cA1代替s，对其作第一步的运算，即可求得cA2和cD2，依此类推。信号s的第j级小波分解具有以下结构：[cAj,cDj,…,cD1]。该过程如图4所示。

waverec函数是通过递归地执行idwt函数来实现的。从第j级的逼近系数cAj和细节系数cDj开始，通过插入零（增采样）并将结果与重构滤波器卷积，逆离散小波变换重构cAj-1。该过程如图5所示。

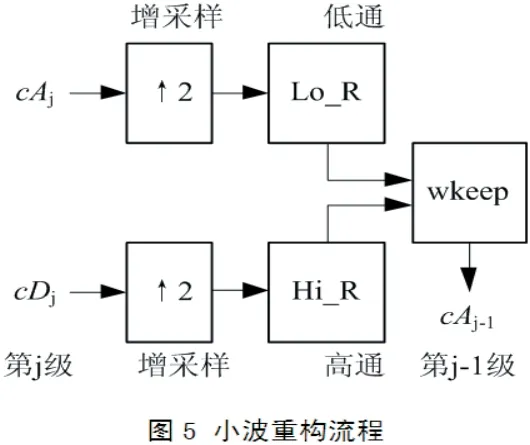
4 小波包分析

4.1 小波包的生成

生成小波包的函数为wpfun函数。在小波工具箱中，当使用正交小波的时候，生成小波包的计算方案：首先，获得对应于小波的2个滤波器h(n)和g(n)，它们的长度为2N；然后，根据方程①和②进行计算，可以得到函数序列(Wn(x),n＝0,1,2,…)。

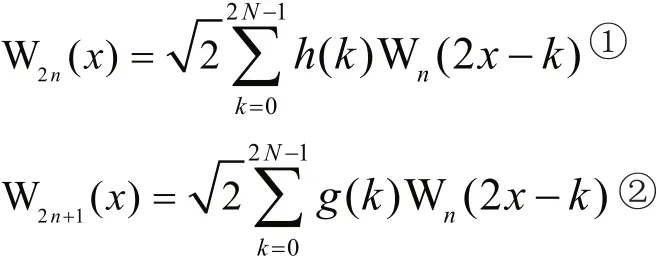
其中，W0(x)＝φ(x)是对应的尺度函数，W1(x)＝ψ(x)是对应的小波函数。

4.2 面向对象的技术

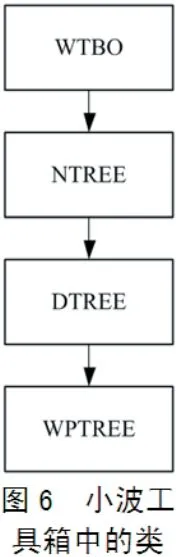
MATLAB支持面向对象的编程范型[4]。在小波工具箱中，一些面向对象的编程特征用于小波包的树结构。在小波工具箱中定义了四类对象：类WTBO（小波工具箱对象），类NTREE（新树），类DTREE（数据树）和类WPTREE（小波包树）。这些对象的层次组织描述如图6所示。

WTBO类是一个抽象类。工具箱中的任何对象都以WTBO为父类，并且继承了WTBO类的方法和域。

NTREE类专用于树操作（如节点标签、节点分割和节点合并等操作），它也是一个抽象类。

DTREE类专用于具有关联数据的树：向量或矩阵。这个类也是一个抽象类，而且这个类的一些方法必须重载。

WPTREE类的目的是管理一维和二维的小波包。小波工具箱使用WPTREE对象用来构造小波包。

5 结论

从小波工具箱的目录结构和源代码出发，深入研究小波工具箱的体系结构和实现技术。小波工具箱实现一维和二维的小波定义、连续小波变换、离散小波变换以及小波包分析等功能。限于篇幅，重点阐述一维的情况。二维的情况可以由一维的情况进行类推。

在小波包分析的实现中，小波工具箱将面向对象的编程范型完美地应用于科学软件，是科学软件开发的一个范例，对学生开发专业软件也具有较大的指导意义。

[1]The Mathworks Inc. Wavelet Toolbox User’s Guide[Z].2009

[2]王大凯,彭进业.小波分析及其在信号处理中的应用[M].北京:电子工业出版社,2006

[3]樊启斌.小波分析[M].武汉:武汉大学出版社,2008

[4]The Mathworks Inc. Object-Oriented Programming[Z].2009