基于D-S证据理论的城市基础设施投资风险评价

李 林，郑惠云，欧婵娟

（湖南大学 工商管理学院，长沙 410082）

1 城市基础设施投资风险的特点

城市基础设施投资具有投资周期长，投资数额大，投资风险高等特点，使得投资的不可预见因素增多，大量的不确定性伴随着风险评价的整个过程，具体表现如下：

(1)风险的动态性。城市基础设施投资项目风险是随环境、条件和自身固有的规律逐渐发展形成的，当城市基础设施投资项目的内部条件或外部条件发生突变时，项目风险的性质和后果会随之发生突变。

(2)风险的多样性和多层次性。城市基础设施投资项目风险因素数量多、种类繁杂，而且大量风险因素之间的内在关系错综复杂、各风险因素之间及与外界交叉影响又使风险显示出多层次性。

(3)风险评价依据的信息是不完全可靠的。城市基础设施投资风险的综合评价是一项复杂的工程，评价过程中涉及到多种因素，对评价所应考虑的因素往往不能够系统全面，这样给出的评价往往缺乏完全自信，只是表达了对结果的一种信念。

(4)风险评价依据的信息是不精确的。城市基础设施投资风险评价大多以定性为主，缺乏客观数据，所用的多是诸如好、差等语言文字表达，不是精确的数据。

(5)风险评价依据的信息有时会相互矛盾。不同的专家对同一项目风险的评价由于知识经验、个人偏好、风险态度的不同，有时会出现评价结果高度冲突的情况，这些矛盾的信息并不是完全错误的，在于如何对这些信息进行恰当的处理。

城市基础设施投资风险的高度不确定性，以及风险评价多采用定性指标，使得传统的风险评价方法应用在城市基础设施投资风险评价中具有一定的局限性，而D-S证据理论在处理不确定性信息和定性指标方面具有较大的优势，为解决这一问题提供了一条有效的途径，从而使评价结果更科学、客观。

2 D-S证据理论及多层次递阶评价模型的建立

D-S证据理论是Dempster在20世纪60年代提出的“上、下概率”及其合成法则的基础上，由Shafer在1976年出版的专著《证据的数学理论》中建立的[1][2]，它是用来处理由人们认识的局限性带来的不确定性问题的有力工具。D-S证据理论能够很好地处理具有模糊和不确定信息的合成问题，DS证据理论核心就是证据合成法则，即D-S法则，其基本思想是：通过辨别框架Θ、基本概率分配m(A)来表示基本支持度，用信任函数Bel(A)和似真度函数Pl(A)来度量不确定性。对于命题A，用区间[Bel(A),Pl(A)]表示对A的信任程度，若有多条证据支持命题A，通过D-S法则计算对命题A的联合支持程度。

2.1 证据源数据的获取

证据源数据的获取一般包括评价指标体系的建立，评价标准的确定以及各评价指标基本支持度的确定[6]。

设S是一个评价对象，评价对象可以分解为n个一级指标：E1,E2,…，En，通常需要继续把一级指标作为一个评价对象，将其分解为r个二级指标：Eij(j=1,2,…，r)。于是，对S的评价过程就形成一个多指标评价的多层次递阶结构，由下到上综合各个指标的评价结果对评价对象S作出价值判断，获得对S的最终评价结果。

在D-S证据理论中，评价标准通常采用序数尺度由若干个评价等级构成，也即评语，如 “好”“较好”“一般”“较差”“差”。 一般地，定义如下的评语集合：Θ={θ1,θ2,…，θm}，其中 θk(k=1,2,…，m)表示指标Eij可能被判定的一个评语。

评价指标的基本支持度是指指标Eij被判定为θk的概率，记为βij。例如有10位专家对指标Eij打分，有6位专家判定 Eij属于 θk，则 βij＝0.6。

2.2 指标权重的确定

在证据理论中，通常采用层次分析法（AHP）确定指标的权重，但层次分析法在检验判断矩阵是否具有一致性方面有一些明显的不足之处。模糊层次分析法的模糊一致矩阵很好的解决了上述问题，满足证据理论中指标权重确定的需要，且更加科学、合理。以下对如何利用模糊层次分析法确定指标权重做一个简单介绍。

2.2.1 建立模糊一致判断矩阵

模糊一致判断矩阵表示针对上一层某元素，本层次与之有关元素之间相对重要性的比较。假定元素C同下一层次中的元素a1,a2,…，an有联系，邀请相关专家对元素a1,a2,…，an相对于上一层元素C进行重要性比较，可得到如下模糊判断矩阵[7]：

2.2.2 计算权重

首先，将上述由K个专家做出的K个比较判断矩阵中的上三角元素组成一个灰色比较矩阵：

其次，对灰色矩阵A(⊗)作白化处理得到比较判断矩阵A，计算公式为：

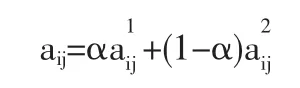
其中，α为灰元的白化系数，其取值范围为：α∈[0,1]。

再次，比较判断白化矩阵A是否具有模糊一致性：如果不满足一致性，可通过灰元的白化系数α来调整比较判断白阵A；如果满足一致性，由模糊一致矩阵的性质可得元素ai相对于其上层元素C的权重：

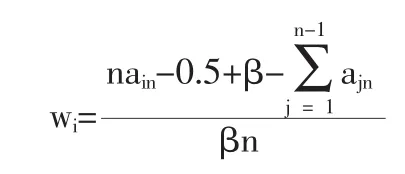
其中i=1,2,…，n，β是对所判断元素的差异程度的一种度量，同测度对象的个数和差异程度有关。

最后，当模糊判断矩阵A不是一致矩阵，而且很难通过调整灰元的白化系数来调整时，可以用最小二乘法求权重向量，计算公式如下[5]：

2.3 基本概率分配（mass函数）的计算

在D-S证据理论中，通常决策者对整个证据只有α的似真度，其中0≤α≤1，参数α的含义大致上反映决策者对指标评价结果所给出的折扣率，即决策者对指标的评价结果不予完全相信，要予以一定的折扣，一般取α＝0.9。下面介绍一种在多层次递阶结构中，如何将折扣率结合指标之间的相对权重将指标的评价结果转化为证据理论中的基本概率分配的方法。

这个方法的关键思想是把关键指标的评价结果作为一个基准，权重最大的指标为关键指标。设关键指标Eik(i=1,2,…，n)对状态 θk(k=1,2,…，n)的概率为 βik，则 mik=αβik(i=1,2,…，n)，表示关键指标对决策者产生的支持程度或信任程度。

对于非关键指标Eik(i=1,2,…，n)对状态θk的概率为βik，由于指标 Eij对指标 Eik的重要程度为 wij/wik，因此对 βij的折扣率为(wij/wik)α，则 mij=(wij/wik)αβik(i=1,2,…，r)，表示非关键指标对决策者产生的支持程度或信任程度[3]。

对任意一级指标Ei，令：

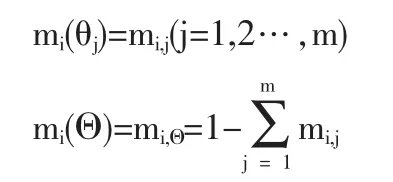
mi,j表示第i个指标Ei支持评价对象a被评为等级θj的概率，mi,Θ是未分配概率，表示不确定程度。

因此我们就建立了指标的mass函数，指标的r个二级指标就构成了一个mass距阵M：

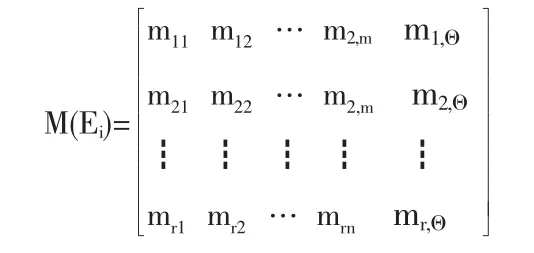
2.4 证据推理的递归合成算法

设 EJ(j)为前 j个因素的集合 EJ(j)={E1,E2,…，Ej}，用 EJ(j),k表示前j个因素支持评价对象a被评为第k个等级的θk程度，mJ(j),k表示前j个因素组合后未被分配的概率。mJ(j),k和mJ(j),k可以通过前j个因素（证据源）合成得到。具体算法为[7]：

其中，kJ(j+1)为归一化因子，它的作用是使 mJ(j+1),k+mJ(j+1),Θ=1，从而避免在证据合成时将非零的概率赋给空集。mJ(j),k=m1,k(k=1,2,…，m)和 mJ(j),Θ=m1,Θ，则由上述递推算法可求出任意 j个因素合成的结果。

3 算例分析

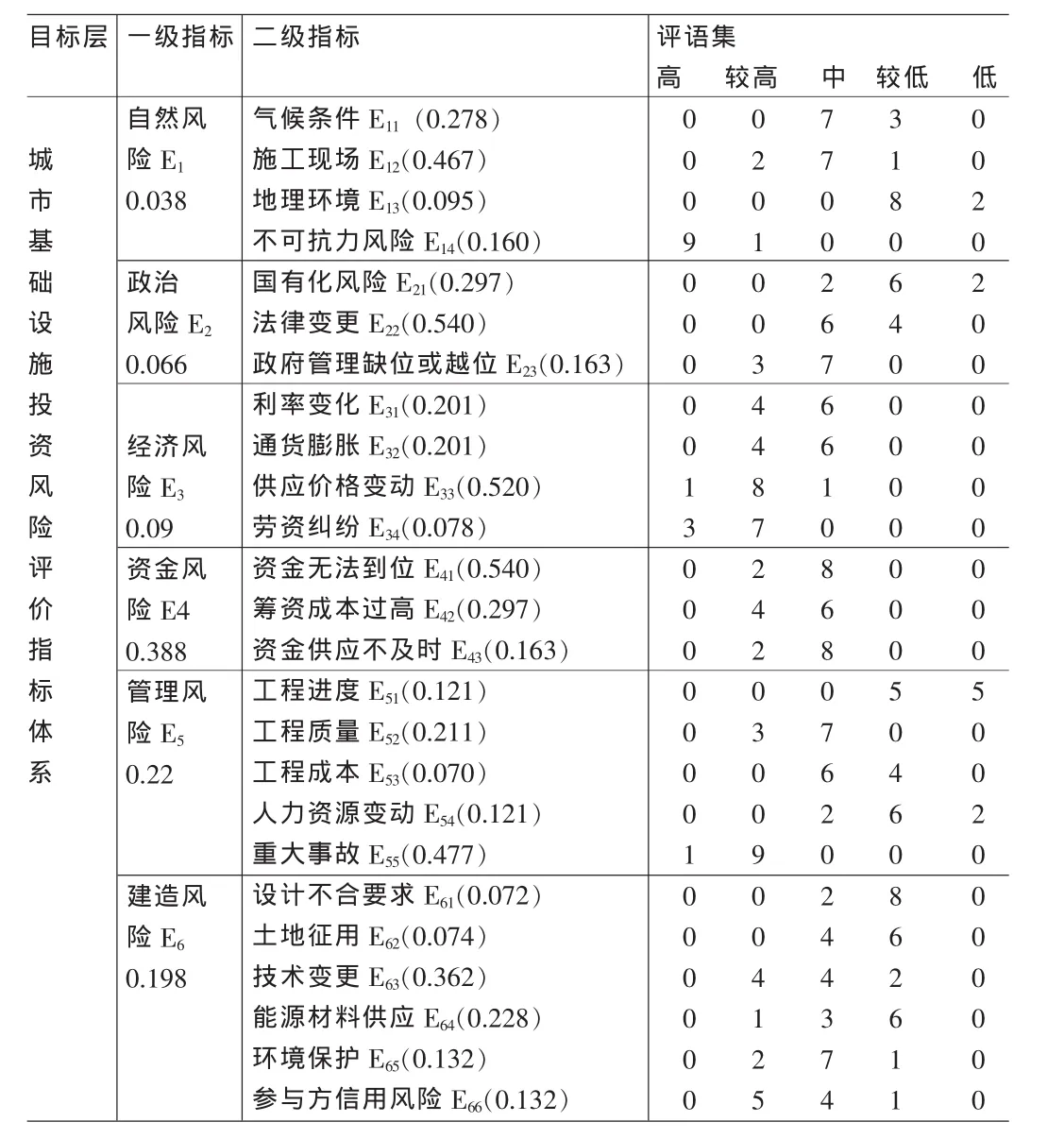
表1

以下结合湖南省某高速公路工程项目说明如何将D-S证据理论运用到城市基础设施投资风险评价中。

3.1 证据源数据的获取

根据城市基础设施项目的风险特点，结合本项目的具体情况建立了如表1的风险评价指标体系。

根据表1所示的评价指标体系，一级指标用Ei(i=1,2,3,4,5,6)表示，E1包含四个因素，表示为 E1(E11,E12,E13,E14)，类似地表示 E2,E3,E4,E5，E6。 用 Θ={θ1，θ2,θ3,θ4,θ5}表示评语集即识别框架，分别表示“高”、“较高”、“中”、“较低”、“低”这五个评语等级。

请10位熟悉该项目和相关领域的专家参加该项目的风险评价，即确定各指标的基本支持度，初始评价结果如表1评语集栏内所示。下面以E1为例说明其含义：在一级指标“自然风险”的四个因素中，对“气候条件”有7位专家评为风险“中”，3位专家评为“较低”；对“施工现场”有2位专家评为风险“较高”，7位专家评为“中”，1位专家评为“较低”；依此类推。其余5个一级指标的含义类似。

3.2 确定指标权重

请10位专家对指标重要性做两两比较，得出模糊一致判断矩阵，再根据指标权重计算方法计算出各指标的权重，计算结果如表1所示，其中一级指标权重向量为W=（w1,w2,w3,w4,w5,w6）=(0.038,0.066,0.09,0.388,0.22,0.198)， 二级指标权重向量表示类似。

3.3 基本概率分配（mass函数）的计算

下面以E1为例，说明如何构造的mass函数。由E1的二级指标权重向量 V1=(v11,v12,v13,v14)=(0.278，0.467,0.095，0.160)可知E12为关键因素，根据基本概率分配的计算方法，对E12其折扣率为 α=0.9， 对 E11，E13,E14其折扣率分别为(v11/v12)α，(v13/v12)α，(v14/v12)α，因此 E1的 mass函数可用下面的矩阵来描述：

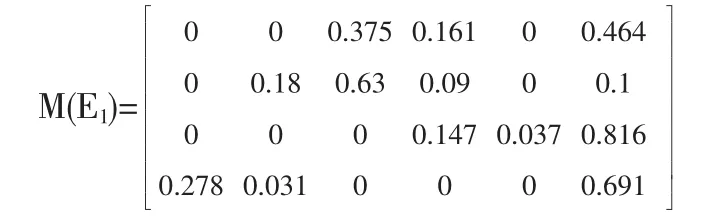
根据2.4节的证据推理递推合成公式，将E1的四个因素的mass函数合成为如下的一个mass函数：

m1(θ1)=0.023，m1(θ2)==0.109，m1(θ3)=0.694，m1(θ4)=0.115,m1(θ5)=0.003，m1(Θ)=0.056

同理可以分别得出 E2，E3，E4，E5，E6的 mass函数

3.4 综合评价

将上述获得的各个一级指标的mass函数合起来就得到一级指标集的评价矩阵：

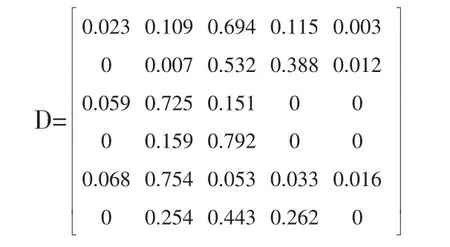
由 W=（w1,w2,w3,w4,w5,w6）=(0.038,0.066,0.09,0.388,0.22,0.198)可知E4为关键因素，其折扣率为α=0.9，E1的折扣率为(w1/w4)α，同理可得 E2，E3，E5，E6的折扣率，用折扣率乘以上面的评价矩阵D的各行就可以得到评价目标的mass距阵：

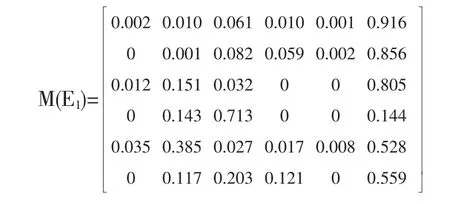
再根据证据推理递推合成公式，将E的六个因素的mass函数合成为目标评价对象的mass函数：

m1(θ1)=0.006，m1(θ2)=0.270，m1(θ3)=0.632，m1(θ4)=0.024,m1(θ5)=0.001，m1(Θ)=0.067

评价结果表明从项目总体来说，专家对该项目的风险为高的支持度为0.6%，为较高的支持度为27%，为中的支持度为63.2%，为较低的支持度为2.4%，为低的支持度为0.1%，无法分配的置信度为6.7%。按照最大隶属度原则该项目的风险评价等级为中。具体来说，“经济风险”和“管理风险”相对于其它因素风险更高，专家对这两个因素的评价都为风险较高，支持度分别为72.5%和75.4%，对这两个风险应予以重点关注。其中对“经济风险”应重点关注“供应价格变动”和“劳资纠纷”这两个风险；对“管理风险”应重点关注“重大事故”和“工程质量”这两个风险。此外，对于作为专家赋予最大的权重的指标“资金风险”为关键风险，投资方也应予以适当关注。

4 结论

城市基础设施投资风险评价是一个涉及众多复杂的、不确定因素的系统工程，评价的最大难度在于对不确定性的处理和定性评价值的量化。本文基于D-S证据理论的思想，提出了一种不确定性下的城市基础设施投资风险评价模型，该模型的基本思路是：首先运用FAHP法确定指标权重，再由指标权重结合基本支持度构造mass函数，然后根据D-S合成法则计算多层次多指标对目标评价对象的联合支持度。最后通过算例表明D-S证据理论能弥补其它评价方法不能很好地处理不确定信息的缺点，适用于城市基础设施投资风险评价具有较大不确定性以及多以定性评价指标为主的特点，评价结果得到专家的认可，利用D-S证据理论对城市基础设施投资风险评价具有一定的有效性和实用性。此外，D-S合成规则有一定的规律，便于电算化，使这一评价方法更具简便性和易操作性。

[1]A.P.Dempster.Upperand LowerProbabilitiesInduced by a Multivalued Mapping[J].Annals of Mathematical Statistics,1967，(38).

[2]Shafer G.A Mathematical Theory of Evidence[M].New Jersey：Princeton University Press,Princeton,1976.

[3]刘爱梅,李光华,周国华.基于证据理论的企业IT部门内部服务质量综合评价[J].科技管理研究,2008,(6).

[4]张吉军.模糊层次分析法(FAHP)[J].模糊系统与数学,2000,14(2).

[5]吕跃进.基于模糊一致性矩阵的模糊层次分析法的排序[J].模糊系统与数学,2002,16(2).

[6]朱卫东,胡云云.基于证据理论的国有企业领导者综合测评研究[J].中国管理科学,2005，(13).

[7]周旭.基于证据理论的我国上市商业银行竞争力评价研究[D].合肥工业大学,2007.

[8]陈斌.BT模式下市政工程建设风险评价研究[D].浙江大学,2006.