重轨矫直参数控制模型的自学习功能研究*

但斌斌，王 超

（武汉科技大学 机械自动化学院，湖北 武汉430081)

作为重轨生产中的最后变形工艺，矫直对提高重轨质量、提高成材率等具有重要意义。为实现对重轨矫直过程参数的精确控制，开发了平直度模型、力能参数模型、工艺参数模型、结构参数模型、应力应变模型和自学习模型等重轨矫直参数控制模型。由于在矫直过程中有许多不确定因素，如变形抗力、重轨表面摩擦系数、表面温度、来料厚度等，其结果会导致矫直压力参数的变化。但因所建立的数学模型带有平均性质，用这样的模型来预报某特定条件下某一重轨的矫直压下量，必然会出现偏差。这种测量值与计算值的偏差，再加上参数检测所带来的测量误差，必然影响模型的预报精度，故需建立一套方法来解决，自学习模型就是为满足这个需求而建立的。

1 重轨矫直参数控制模型

平立复合矫参数模型是矫直过程中各参数和变量之间所存在的某种数量相互之间的关系，采用形式化语言，概括或近似表达出来的一种数学结构。通过科学理论和生产实践，研究建立重轨钢矫直过程中理论统计型模型的方法和程序。

平立复合矫参数模型的基本任务是根据来料条件及对成品的要求，通过数学计算参数模型的计算，确定各辊的位移量、矫直力、速度等，以保证获得尽可能符合要求的重轨钢成品。模型计算流程如图1所示。

根据图1所示的计算要求可知，平立复合矫参数模型包含如下几个部分：

（1）结构参数模型，用于计算和分析平立复合矫直过程中的辊径，由此确定各辊预压下量，是最重要的控制模型之一。

（2）力能参数模型，用于计算矫直力和工作转矩。

（3）工艺参数模型，用于计算和分析平立复合矫各辊的压弯量。

（4）平直度模型，计算在初始设定参数的情况下，模型能够得到的矫直效果。

（5）自学习模型，从数据库中存储的历史数据中智能学习参数相互之间的关系，给出优化的调整值。

（6）应力应变模型，为自学习模型实现智能化提供样本数据库支持。

2 自学习模型的建立

为实现自学习功能，需要建立一个自学习数学模型，要提高模型的精度，需要运用所获取的数据，对数学模型不断进行修正。然而，在实际过程中，运用所获取的数据来判断被监测对象的状态是一种复杂的非线性推理过程，在这一过程中难以建立明确的数学模型，且随着系统复杂度的增大，输入与输出之间的规则难以建立和维护。因此，ANN被引入使用。

2.1 人工神经网（ANN）的应用

由于ANN不需要预先给出有关模式的经验知识和判别函数，能对来自不同状态的信息逐一进行训练而获得某种映射关系，因此它在模式识别领域的应用越来越广泛。ANN不仅可根据样本进行学习，改善模式识别能力，而且无需对模式分布进行一些统计上的假设，突破了传统智能算法技术的束缚。

自学习的过程实际上是把征兆空间的向量映射到解空间的过程。假设征兆空间为X，解空间为Y，自学习的工作即实现空间X到空间Y的映射F：

通常，映射F是未知的，并且难以用明确的数学模型来描述，但ANN可以通过学习输入到输出的样本集，实现输入到输出的映射关系，其作用可用图2表示。

在图 2中，x和 x′为输入空间的样本，y和 y′为输出空间的样本。用部分已知输入样本x和输出样本y对ANN进行训练，训练后的网络可以学会输入样本与输出样本之间的内在联系，并把这种“知识”存储在各神经元的连接权值上。训练好的网络可用来替代映射关系F，完成已知输入样本x′到未知输出样本y′的映射。采用ANN实现自学习的关键点是输入输出样本集的构建和神经网络训练算法的选择。

运用神经网络进行故障诊断时，需要大量的输入输出样本来构成样本集，神经网络通过对样本集中数据的训练来学习输入和输出之间的映射关系。

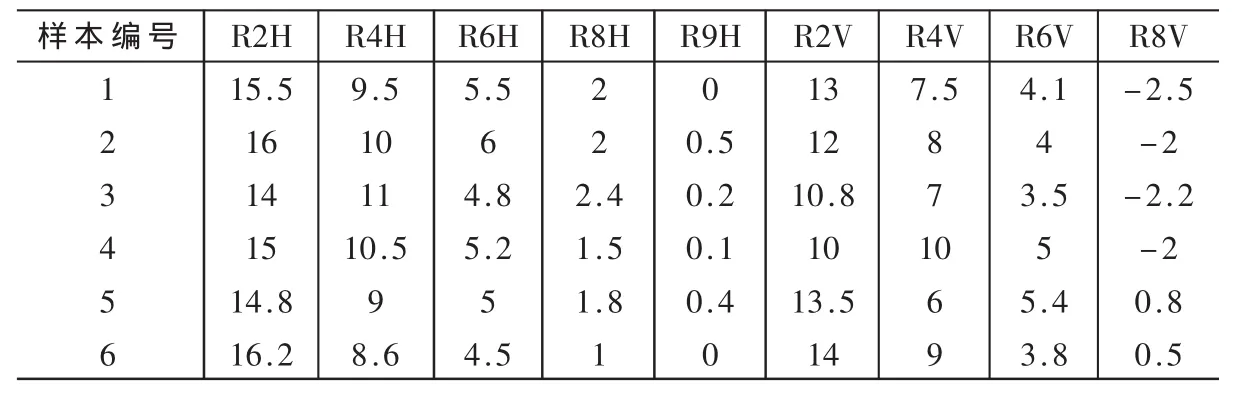
表1 60 kg/m输入样本

表2 60 kg/m输出样本

以60 kg/m重轨钢为例，用水平矫中 2号辊（R2H）、4号辊（R4H）、6号辊 （R6H）、8号辊 （R8H）和 9号辊（R9H），以及垂直矫中 2号辊（R2V）、4号辊（R4V）、6号辊（R6V）和 8号辊（R8V）的压下量作为网络的输入，用上述辊对应的调整系数（如水平矫中2号辊的调整系数为R2HC）作为输出，通过现场记录的数据，形成神经网络输入输出样本集，建立了训练样本输入输出表，部分数据如表1和表2所示。表中的数据可用来指导神经网络的训练。训练好的ANN可用于预测下次计算模型的分配系数，从而得出一个较优的初始压下量输入值。

2.2 RBFNN训练算法

本项目提出采用RBFNN作为神经网络的训练算法。

RBFNN结构与BPNN结构类似，也是由输入层、隐层和输出层组成的前馈网络，其结构如图3所示。对于从X→Y的映射，RBFNN可写为：

图3 RBFNN结构

式中，qi为第 i个隐层节点的输出，X=(x1，x2，…，xn)为输入样本，ci为第 i个隐层节点的中心，m为隐层节点的个数 ，||·||为欧式范数，p为输出层的节点数，wki为第 i个隐层节点到第k个输出层节点的连接权，R为径向基函数。径向基函数通常采用高斯核函数：

式中，σi为第 i个隐层节点的宽度。由式(4)可知，隐层节点对输入信号在局部产生响应，即当输入信号靠近径向基函数的中央范围时，隐层节点将产生较大的输出。

在RBFNN中，各隐层节点的输出实际代表着输入样本X离开该节点的径向基中心ci的程度。隐层的训练任务不是调节其权矩阵，而是为每个隐层节点选择其中心向量。

RBFNN的学习过程包括隐层参数的确定和输出层参数的确定两个不同的阶段。隐层参数包括隐层节点数m、各隐层节点的中心值 ci和宽度参数σi，一般采用无监督的K-Mean算法；输出层参数包括输出层的权值wki，一般采用有监督的 OLS算法(正交最小二乘法)。算法步骤为：

(1)初始化各个聚类中心ci(i=1，2，…，m，m为聚类个数，亦为隐层节点的个数)；

(2)将输入信号进行相似匹配，其条件是它与中心的欧式空间距离最小，即：

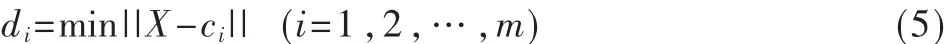
(3)归类完毕后，求出每个归类的新中心 ci和宽度，分别表示为：

以上三步完成了聚类，从而确定了隐层参数，接着进行输出层的最小二乘法训练；

(4)设分类器的输出规定为：

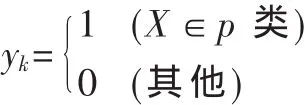
定义网络输出的误差函数为：

式中，ok为输出单元k的期望输出，yk为实际输出。将式(3)代入式(8)，有

训练输出层的目的是要找出一组权值wki，使得误差函数为最小，因此令

将式(9)代入式(10)，可以求得合适的权值wki。

采用上述步骤可以确定RBFNN的网络结构参数，用表1和表2中的样本数据对其训练后可以用于平立复合矫各辊的压下量调整系数的计算。

从重轨参数控制模型中的计算模型得出矫直的初始压下量，当不能满足矫直的工艺要求时，自学习模型采用RBFNN算法从数据库中存储的历史数据中智能学习参数相互之间的关系，给出优化的调整值，使得矫直控制模型能很好地控制重轨的矫直工艺，并在实际应用中取得很好的效果。

[1]崔莆.矫直理论与参数计算(第二版)[M].北京：北京工业出版社，1994.

[2]于凤琴，于辉，杜凤山.复合重轨矫直机的矫直力计算[J].燕山大学学报，2005，(29)：448-450.

[3]吴洪岩，刘淑华，张嵛.基于RBFNN的强化学习在机器人导航中的应用[J].吉林大学学报，2009，27（2）：185-190.