Markov网页预测模型综述*

2010-05-18刘超慧吴庆涛

网络安全与数据管理 2010年18期

刘超慧,吴庆涛

(1.郑州航空工业管理学院计算机科学与应用系，河南郑州 450015;2.郑州航空工业管理学院计算中心，河南郑州 450015)

建立有效的用户浏览预测模型，对用户的浏览做出准确的预测，是导航工具实现对用户浏览提供有效帮助的关键。

在浏览预测模型方面，很多学者都进行了卓有成效的研究。AZER[1]提出了基于概率模型的预取方法，根据网页被连续访问的概率来预测用户的访问请求。SARUKKAI[2]运用马尔可夫链进行访问路径分析和链接预测，在此模型中，将用户访问的网页集作为状态集，根据用户访问记录，计算出网页间的转移概率，作为预测依据。SCHECHTER[3]构造用户访问路径树，采用最长匹配方法，寻找与当前用户访问路径匹配的历史路径，预测用户的访问请求。XU Cheng Zhong等[4]引入神经网络实现基于语义的网页预取。徐宝文等[5]利用客户端浏览器缓冲区数据，挖掘其中蕴含的兴趣关联规则，预测用户可能选择的链接。朱培栋等人[6]按语义对用户会话进行分类，根据会话所属类别的共同特征，预测用户可能访问的文档。

在众多的浏览模型中，Markov模型是一种简单而有效的模型。Markov模型最早是ZUKERMAN[7]等人于1999年提出的一种用途十分广泛的统计模型，它将用户的浏览过程抽象为一个特殊的随机过程——齐次离散Markov模型，用转移概率矩阵描述用户的浏览特征，并基于此对用户的浏览进行预测。之后，BOERGES[8]等采用了多阶转移矩阵，进一步提高了模型的预测准确率。在此基础上，SARUKKAI建立了一个实验系统[9],实验表明，Markov预测模型很适合作为一个预测模型来预测用户在Web站点上的访问模式。

1 Markov模型

1.1 Markov模型

Markov预测模型[10]对用户在Web上的浏览过程作了如下的假设。

假设1(用户浏览过程假设)：假设所有用户在Web上的浏览过程是一个特殊的随机过程——齐次的离散Markov模型。即设离散随机变量的值域为Web空间中的所有网页构成的集合，则一个用户在Web中的浏览过程就构成一个随机变量的取值序列，并且该序列满足Markov性。

一个离散的Markov预测模型可以被描述成三元组＜S，A，B＞，S代表状态空间；A 是转换矩阵，表示从一个状态转换到另一个状态的概率；B是S中状态的初始概率分布。其中S是一个离散随机变量，值域为{x1，x2,…xn}，其中每个xi对应一个网页,称为模型的一个状态。

Markov预测模型是一个典型的无后效性随机过程，也就是说模型在时刻t的状态只与它的前一个时刻t-1的状态条件相关，与以前的状态独立。即：

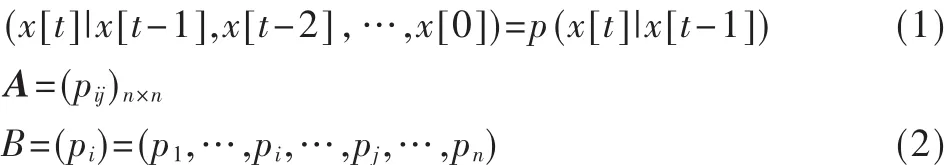
一个Markov预测过程可以由它的转移矩阵和初始分布向量确定，其中转移矩阵集中描述了该Markov链预测模型的动态特征。该预测模型的转移概率矩阵用A表示，初始分布向量用B表示，如式(1)、式(2)所示。

其中pij表示在矩阵中,页面xi到页面xj的转移概率，即：P(Xt=xj|Xt-1=xi)；Pi表示初始概率分布。

用向量 H(t)=(0,…，1,…)表示用户在时刻 t的状态，如果用户在t时刻访问的页面为x，则用户在向量的第i维就是1，其余为零。用向量M(t)表示时刻t时的状态概率向量，M(t)=P(Xt=x1)，P(Xt=x2),…P(Xt=xn))表示在t时刻不同状态的概率,t时刻用户访问状态可表示为：

根据式(3)将得到一个 n=|H(t)|的向量 M(t)，其中概率值最大的那一维就是用户在t时刻的最有可能的状态，式(3)中A即为一阶Markov模型状态转移矩阵。

在许多应用中，一阶Markov预测模型不能很准确地找到用户将要访问的页面。这是由于这些模型没有细致地考虑用户的访问历史，所以不能很好地区分不同用户的行为模式。为了得到较好的预测结果，一般偏向于使用二阶以上高阶的Markov预测模型，其基本公式如式(4)所示：

其中Ak是 k阶状态转移矩阵，H(t-k)为过去的(tk)时刻的状态向量，此时M(t)表示的是k阶Markov模型的预测状态。

1.2 性能指标

为了评测Markov模型的性能，常使用以下两个性能指标。

定义1:预测精确率P

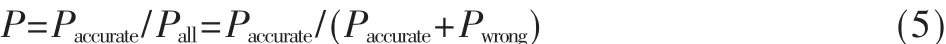
即，预测精确率P表示正确预测的Web对象数与预测Web对象数的比率。其中，Paccurate为预测结果中至少有一个在当前请求后时间窗口内被请求的次数；Pall为总预测次数，它表述了模型的准确程度。

定义2：覆盖率A

即模型能使用的次数占总申请次数的百分比。其中，Pall为总预测次数,Precord为记录总数，它描述了模型的预测能力，反映了模型的可用性。

2 扩展预测模型

2.1 隐Markov预测模型

隐Markov模型最早由BAUM提出，在许多领域，尤其是语音识别中得到了广泛的应用。先用隐Markov模型对用户进行分类，然后针对具有不同类别的用户提炼出不同的预测模型[11],是隐Markov模型的一种具体应用。采用离散化输出一阶隐马尔科夫模型，模型可以表示为λ=(A，B，π)，式中：A 为状态转移概率分布，A={aij|1≤i,j≤N}，aij=P[qt|qt-1=i];B为输出符号的概率分布，B={bj(k)|1≤k≤M,1≤j≤N},bj(k)=P[ot=vk|qt=i];

Π为初始状态概率，π={πi|1≤i≤N},πi=P[q0=i]

N为状态个数，t时刻状态表示为qt;

M为离散输出符号个数，输出符号集V={v1,v2…vM}

给定 A，B，π，N，M 的隐 Markov模型可以产生序列O=(o1,o2…on),oi为状态输出符号。假设状态序列其q=(q1,q2,…,qn)已知，则观察序列O的概率为：

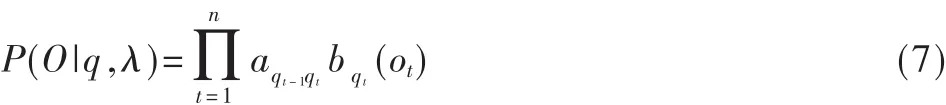
王实[12]等提出一种新的基于隐马尔可夫模型的兴趣迁移模式发现方法，并利用用户迁移模式间的关联规则来发现兴趣迁移模式。而借助隐马尔可夫模型,挖掘蕴涵在用户访问路径中的信息需求概念,以此进行预取页面的评价,也可以实现基于语义的网页预取[13]。

隐Markov模型尽管考虑了用户兴趣,但和简单的Markov模型一样，存在一定的不足：用户访问序列串长是动态时变的,采用固定阶数的传统Markov链模型并不能准确地对用户的访问行为建模。

2.2 多Markov模型

虽然用户在Web空间的浏览过程是一个受浏览目的、文化背景、兴趣爱好等多种因素影响的复杂过程,有很多差异，然而观察大量用户的浏览过程可以发现，某些用户的浏览过程表现出相同或相近的特点，如他们浏览的网页基本相同，浏览各个网页的顺序相似等，这一现象引发了对Web用户分类的研究。通过对用户分类，同一类别的用户用同一个模型来描述它，而不同类别的用户其浏览过程差别较大，用不同的模型来描述他们的特征则更为合理[14]。

假设 2(用户分类假设)：假设根据用户在 Web空间的浏览特点,可以将所有用户分为K类。如果用C={c1,c2,…,ck}表示用户的类别，则任意一个用户属于类别ck的概率为P(C=ck),而且有：

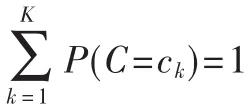
假设 3(类 Markov链假设)：假设同一类别的用户具有相同或相近的浏览特征，且其浏览过程是一个特殊的随机过程——齐次离散Markov链。基于这两条假设建立用户浏览预测模型，并把这种基于用户分类的含有多个Markov链的模型称为多Markov链模型。

定义3：多Markov链模型可以表示为一个四元组

＜X，K，P(C)，MC＞。其中，X 是一个离散随机变量，值域为{x1,x2,…,xn}，每个 xi对应一个网页，称为模型的一个状态；K表示模型包含的用户类别的数目；C={c1,c2,…,ck}表示用户的类别，其分布函数P(C)表示不同类别用户的概率分布；MC={mc1,mc2,…,mck}为类 Markov链的集合，每一个元素mci是描述类别为ck的用户浏览特征的Markov链,称为类Markov链,它的转移矩阵可以表示为：

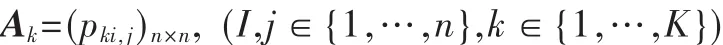
对多模型的学习主要是确定以下几个参数:

(1)用户类别数K;

(2)任意一个用户属于类别ck的概率P(C=ck);

(3)类Markov链的转移矩阵。

实验证明这样就克服了单Markov链模型中用一个Markov链描述所有用户的浏览特征而带来的不准确性，从而更精确地描述用户的浏览特征，并有希望得到更高的预测准确率。

多Markov链模型的时间复杂度较高，在处理一个包含m个用户浏览序列和n个网页的日志文件时，其时间复杂度达O(m5n2)。如果日志文件较大，m和n的取值也会很大，因此，多Markov链模型的时间消耗极大。

2.3 混合Markov模型

多Markov模型充分考虑了不同用户间的差别，但对于个体没有考虑请求在时序上的先后，没有考虑请求的网页之间的内在联系。混合Markov模型能克服类似的不足。

假定用户的浏览模式满足简单的Markov性下，则下面两式成立：

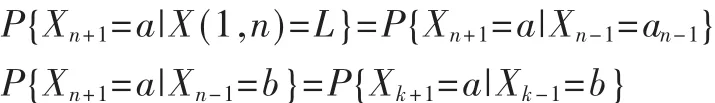
以上两式中ak代表了具体的一个网页W，L=a1,a2,…,an-1,an代表用户所经历的W序列。X(i,j)表示随机变量序列(Xi,Xi+1,…,Xj-1,Xj)，其中 i≤j。

上述模型称为二步Markov模型[15]，它的核心任务是建立一个与一阶Markov模型的转移概率矩阵同规模的转移概率矩阵。矩阵的行元素代表用户浏览的上一个网页，列元素代表用户下一步可能浏览的网页。通过该矩阵可以根据用户上一步浏览的网页来预测下一步要浏览的网页。

定义4:混合模型表述如下

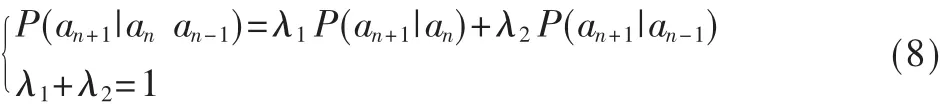
(8)式中的λ1、λ2分别是一阶模型和二步模型的混合系数。混合模型的关键就是根据极大似然函数定理求出λ1和λ2。

在多Markov模型方面,刘业政等[16]提出可变多阶Markov链模型VMOMC。VMOMC将用推荐目标网页概率值度量的可变多阶Markov链并行组合，组合模型中采用遗传算法确定各单阶Markov链模型的最优权重。陈佳[17]提出了基于混合模型的一种挖掘用户群在页面上兴趣分布程度的模式发现，计算用户群从一个页面到另外一个页面的导航路径模式的概率大小，可得到大量的用户对所访问Web的兴趣及导航模式,从而预测用户的浏览路径。

2.4 结构相关性模型

有研究表明，用户在进行Web浏览的绝大部分时间里都是从当前页面中挑选一个链接继续浏览；在用户将来访问的网页中，46%能在最近3个网页的链接中找到，75%能在所有历史网页的链接中找到。因此，可以认为用户将来的可能请求大部分存在于由当前页面上所有链接组成的集合中。基于结构相关性的一阶Markov模型包括以下三部分[19]：

(1)用户访问序列集合：一个序列是指用户在一段连续时间内先后访问的一系列网页，记作Seq={sm},sm=＜pml,…,pmn,…,＞(m=1，2，…M，M 为序列个数；n=1，2，…，Nm，Nm为序列 s中网页的个数)。

(2)用户状态集合：即用户访问序列集合中所有节点网页组成的集合，记作 Stat={p1,…,pi,…}(i=1，2,…I,I为状态个数)。显然Seq中每一个pmn都在Stat中有一个对应的 pi。

(3)状态转移概率：记作tij=P(pj|pi)，表示用户从当前网页pi转至访问网页pj的概率。

用有向图G=(P，E)描述基于结构相关性的Markov模型。其顶点 pi(pi∈P)为用户状态，有向边 eij(eij∈E)表示用户曾从pi根据链接访问pj。另外还要为pi定义一个链接集合p.Link，表示网页 pi上包含的所有链接；为 pi的每条eij定义一个计数器eij.Count，表示用户从网页pi转至访问网页pi的次数，并用它来代替用户的状态转移概率tij。

通过遍历用户访问序列的节点，可以得到用户的状态空间和转移情况，并最终建立上述模型。

结合页面内容及站点结构来调整状态转移矩阵,以获得更精确的预取结果,提高Web服务的质量[20]。而利用频繁访问模式树存储Markov链，能够大幅减小存储空间[21]。

3 进一步研究的问题

尽管现有的Markov浏览预测模型在预测准确率、覆盖率方面已取得较满意的成果,但浏览预测问题的实际应用背景中的一些特殊要求使得这一领域仍存在一些需要进一步研究的问题。这些问题包括:

(1)Markov转移概率矩阵的处理。该模型的存储空间主要用于保存状态转移概率矩阵，所以其存储空间的复杂度是网页数目n的平方，即为0(n)。由于n的值一般都比较大，存储复杂率较高。同时为了提高Web预取的命中率，常常联合多个Markov链模型，即用到了多阶状态转移矩阵，使得存储复杂率成倍提高。因此如何存储及处理Markov模型的概率矩阵、降低复杂度是急需解决的问题。此外，在很多情况下状态转移矩阵是稀疏矩阵，采用什么样的数据结构来存储这样的矩阵也是需要研究的课题。

(2)混合Markov模型的求解问题。混合Markov模型在预测用户的浏览行为方面越来越受到学者的重视。有效的模型求解方法，能大大提高模型的效率。虽有学者[15，22]进行了有益的探索，但这方面的工作仍需要更多学者的参与。

(3)在实际浏览预测问题中,Markov的随机统计方法与其他方法,如神经网络、贝叶斯网络、聚类、关联规则、遗传算法等相结合能获得较高的预测准确率。

(4)用户在Web空间的浏览过程是一个受浏览目的、文化背景、兴趣爱好等多种因素影响的复杂动态过程，如能有效地度量用户的浏览兴趣，并及时发现用户的兴趣迁移[25]，对于提高预测准确率非常重要。此外，随着无线网络的普及，怎样预测无线网络环境下用户的浏览行为，是研究人员面临的又一个课题。

全文概述了基于Markov的各种预测模型，分析了各个模型的原理及优缺点，指出了今后的研究方向。

[1]BESTRAVROS A.Using speculation to reduce server load and service time on the WWW proceedings of the CIKM′95,Baltimore,1995：403-410.

[2]SARUKKAI R.Link prediction and path analysis using Markov chains[J].Computer Networks,2000,33(1-6):337-386.

[3]SCHECHTER S,KRISHNAN M,SMITH M D.Using path profiles to predict HTTP requests[J].Computer Networks and ISDN Systems,1998，30(1-7):457-467.

[4]XU C Z,TAMER.Semantics-based personalized prefetching to improve Web performance[C].Proceedings of the 20th IEEE Conference on Distributed Computing Systems,2000:636-643.

[5]徐宝文，张卫丰.数据挖掘技术在Web预取中的应用研究[J].计算机学报,2001,24(4)：10-17.

[6]朱培栋,卢锡城,周兴铭.基于客户行为模式的 Web文档预送[J].软件学报,1999,10(11)：1142-1147.

[7]ZUCKERMAN I D.Albrcht predicting user’s requests on the WWW[C].In:Proceedings of the 7th International conference on User Modeling,New York,springer,1999:275-284.

[8]BORGES J,LEVENE M.Data mining of user navigation patterns.In:Proceedings of the1999 KDD Workshop on Web Mining,CA:Springer Verlag Press,1999:92.

[9]SARUKKAI R.Link prediction and path analysis using Markov chains[C].Amsterdam,Nether-lands Proceedings of the 9th World Wide Web Conference,2000:234-247.

[10]林文龙,刘业政,姜元春.Web浏览预测的Markov模型综述[J].计算机科学,2008,35(1):9-14.

[11]金民锁,刘红祥,王佐,基于隐马尔科夫模型的浏览路径预测[J].黑龙江科技学院学报,2005,15(3):167-170.

[12]王实,高文,李锦涛,等.基于隐马尔可夫模型的兴趣迁移模式发现[J].计算机学报,2001,24(2):152-157.

[13]许欢庆,王永成,孙强.基于隐马尔可夫模型的Web网页预取[J].上海交通大学学报,2003,37(3):404-407.

[14]刑永康,马少平.多Markov链用户浏览预测模型[J].计算机学报,2003,26(11):1510-1517.

[15]余雪岗,刘衍珩,魏达,等.用于移动路径预测的混合Markov模型[J].通信学报,2006,27(12):61-69.

[16]刘业政,林文龙.可变多阶 Markov链模型及在 WWW 个性化推荐中的应用[J].情报学报,2008,27(6):819-824.

[17]陈佳,吴军华.基于混合Markov模型的用户浏览预测[J].计算机工程与设计,2009,30(4):903-906.

[18]叶海琴,石磊,王意锋.基于网络访问行为的混合阶Markov预测模型[J].计算机工程与设计,2008,29(2):333-336.

[19]张丽,郭成城.基于结构相关性Markov模型的Web网页预取方法[J].计算机工程与应用,2O04(2):163-167.

[20]徐燕.基于内容和结构的Markov模型在网页预取中的应用[J].计算机工程与科学,2007,29(4):25-27.

[21]闫永权，张大方.基于频繁的 Markov链预测模型[J].计算机应用研究,2007,24(3):41-43.