轻同位素分离级联系统的简捷设计

许保云,李虎林,袁家均,李良君,杜晓宁

(上海化工研究院 上海稳定同位素工程技术研究中心,上海 200062)

在实际的同位素分离工艺中,同位素的浓缩是在由多个分离级按一定的方式组成的级联系统中完成的,级联的每一级由一定数量的分离器串联而成。如何设计出一个最经济的级联来获得所需的目标同位素产品是人们很关注的课题,有关这方面的理论称为级联理论。级联的计算问题特别是多组分级联的计算相当复杂,参数和目标值之间没有显式的表达式,对较大规模级联系统的计算也相当耗时。如何选择适宜的级联参量实现级联系统的最优化是值得探讨的课题[1-2]。轻同位素和稀有气体同位素的分离主要采用蒸馏法、化学交换法和热扩散法,这些分离方法所用设备均为普通的塔型设备,因此,本工作以塔型设备的分离级联系统为例,通过建立简单通用的数学模型,采用均匀试验设计的方法求取级联参量的最优值。

1 稳态级联的基本参量

塔级联是由多个塔串联联接而成的。塔级联中浓度低的部分由于处理的物料流量大,所以塔径大,有时也采用多个塔并联的形式。浓度高的部分流量小,因此塔径也比较小,这种塔级联很像阶梯,所以又称为梯形级联。梯形级联根据是否有提取段又分为完整级联和开口级联,其结构示意图示于图1。

对于级联的富集段而言,稳态操作时,无论在哪个塔上任取一截面,根据物料守恒和同位素守恒都可以得到L-G=P和Lx-Gy=P x p,其中,L为液相流量;G为气相流量;P为产品流量;W为废料流量;Px p=j就是级联的同位素产率。稳态级联产率Pxp的获得是依靠级联顶部(富集段)进出的两股同位素流的差额 L1 x f-G1y w供给的,塔径确定后,L1和G1可认为是不变的,原料浓度 xf固定,但yw却是与塔的传质效果有关。如果塔的传质效果极差,或塔的理论板数太少,气液两相间几乎不会发生同位素转移,此时废料中y w几乎等于 x f,则级联的产率几乎等于零;如果塔的传质效果十分好,或塔的理论板数非常多,就可以明显降低 y w的值,从而提高级联的产率。当y w降至与 x f平衡时的y f,e时,产率可达最大值 j 0,但是要实现 y w=y f,e,需要无限多的理论板数,这在实际操作中是无法实现的,因此j0也就成为j的极限值。将实际级联中同位素传递量j与级联系统极限传递量j0的比值定义为相对抽取率θ,它表示级联的负载程度。但θ值与多种因素有关,因此在级联设计中要对各影响因素进行仔细考量。

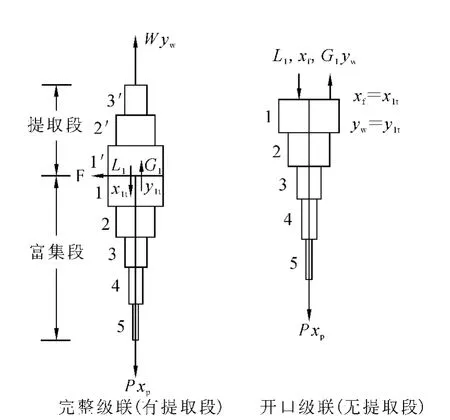
图1 同位素分离的级联系统示意图L——液流;G——气流;F——原料流;P——产品流;W——废料流;x f——原料浓度;y w——废料浓度;x p——产品浓度

定义各级的塔釜重馏分中的关键组分与塔顶轻馏分中的关键组分浓度之比为级的浓缩系数q。对于级联每塔富集倍数q的划分,最简单的方法是选择各级的富集倍数相同,即:

qi=qT1/m

其中qi为第i级的富集倍数,qT为级联系统的总富集倍数,m为级联系统的级数。但是在求整个级联系统的最佳化条件时,应分别计算各级的富集倍数。

级联的相对抽取率θ和关键组分的富集倍数q是设计同位素分离级联系统的关键参量,选定θ和q之后,结合原料组分的浓度、产品浓度、产量以及组分间的相对挥发度可以计算出各塔的气、液相流量以及理论板数,从而进行级联各塔的设备费用和操作费用的计算。

进行同位素分离的级联系统的研究就是通过分析级联系统的稳态过程,得到最佳化工作参量,使得级联系统的设备费和操作费最低[3]。

2 目标函数的建立

优化法是以一定的设计要求比如经济性作为目标函数,以回流比、理论板数、持液量等参数为决策变量,进行优化计算。级联的优化可以通过实验研究和数学模拟来进行,但是同位素分离实验的难度大、成本高,而且很耗时。因此,需要对级联系统建立恰当的数学模型,通过对模型的深入研究为级联系统的设计和优化提供参考。

本工作拟通过对级联系统进行分析提出同位素分离级联系统的优化设计模型,考察的指标为级联系统的年总费用J(包括设备折旧费和操作费用),采用的决策变量为各级的相对抽取率和关键组分的富集倍数。目标函数的数学表达式为[4-6]:

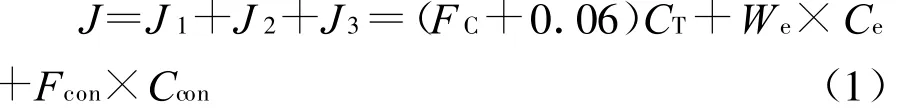
(1)式中,F C为塔设备年折旧率,设备寿命一般为8～10年,故F C=1/8～1/10,a-1;C T为精馏塔设备费,万元;W e为加热需要的能量,度;C e为电费,元/度;F con为冷凝介质的消耗量,升/年;Ccon为冷凝介质的单价,元/升;0.06为维修费,取设备费用的6%。

3 实例分析

各塔相对抽取率和富集倍数是在级联的工艺计算中非常重要的级联参量。相对抽取率表示级联的负载程度,提高级联的相对抽取率,可以减小塔内的液体流量,降低操作费用,但是若要保持级联的富集倍数不变,就需要增加级联的理论板数,设备费用会相应增加,因此需要选择适宜的级联相对抽取率使得总成本最低。以低温精馏法制备高丰度13CO同位素的三级联系统为例,采用均匀试验设计的方法进行级联系统的优化[7-9]。

优化过程中,供料为天然丰度的CO。CO原料各组分的丰度分布列于表1。

表1 CO原料的各组分丰度分布

设计时,要求提取塔塔顶产品中13C的丰度为0.5%,第三级塔塔釜产品中13C的丰度为82%,级联系统中共有第一塔相对抽取率、第二塔相对抽取率、第三塔相对抽取率、第一塔的富集倍数、第二塔的富集倍数这5个变量,计算过程中选用五因素十五水平的均匀设计方案进行级联系统的优化。设计方案及实验结果列于表2。

表2 五因素均匀设计表及实验结果

对表2的数据用DPS软件数据处理系统进行二次多项式逐步回归分析,并对该模型进行显著性检验,得到的回归方程为:Y=227.07-212.17X 1-13.52X2-19.66X 3-7.90X 4+102.49X 1×X 1-0.68X 4×X 4+18.31X 1×X 3-4.16X 1×X 4+0.14X 1×X 5+5.93X2×X3-0.28X2×X4+2.40X3×X4-0.0754X3×X 5(模型Ⅰ)。

由回归方程得到当Y取极小值时,五因素最佳值分别为 :0.95、0.95、0.60、5.5、5.0,Y 最低时,采用回归方程预测,年总费用为 Y=69.27万元,均低于均匀试验中15组结果,这说明优化结果对于重要的级联参量的选择具有一定的指导意义。利用回归方程预测的参数进行计算得到其对应的年总费用为74.969 2万元,模型预测值与实际值相对误差为7.6%。由于模型预测的最低费用与实际费用之间的相对误差比较大,且预测的最佳参数均为边界值,造成预测的结果不可靠。因此将上述最佳参数和其对应的实际年总费用补充到均匀设计表中,重新对均匀设计表中的实验结果进行回归得到模型方程:

该模型预测Y取极小值时,五因素最佳值分别为:0.95 、0.88、0.69、5.5、8.4,计算得到第三级的富集倍数为1.6,Y最低时回归模型预测的年总费用为Y=74.313 4万元。使用回归模型Ⅱ预测的参数进行计算得到其对应的年总费用为74.430 6万元,模型Ⅱ的预测值与实际值相对误差为0.2%,这说明回归模型的预测精度大幅提高了,因此采用第二组数据进行该分离过程的级联设计。

4 小 结

以级联系统的年总费用为目标函数,以各分离级的相对抽取率、关键组分的富集倍数为决策变量建立目标函数,采用均匀试验设计的方法对低温精馏法制备高丰度13CO的三级联系统进行关键参量的优化。通过使用DPS软件数据处理系统对均匀试验结果进行回归分析,得到了级联系统年总费用对各级联参量的数学模型,并求出当年总费用达到最小值时,将天然丰度为1.1%的13CO富集到82%的三级联系统的各级相对抽取率和富集倍数分别为 0.95、0.88、0.69、5.5和8.4,计算得到第三级的富集倍数为1.6。

致谢:对上海化工研究院的徐静安教授和陈大昌教授的悉心指导表示衷心感谢。

[1] Andreev BM,Magomedbekov EP,Raitman AA,et al.Separation of isotopes of biogenic elements in two-phase systems[M].Duch:Elsevier,2007:217-244.

[2] 谢全新,李大勇,李文泊,等.多组分同位素分离级联的优化[J].核科学与工程,2008,28(1):86-91.

[3] 杨国华,曾权兴.稳定同位素分离[M].北京:原子能出版社,1989:212-262.

[4] 阮奇,叶长燊,黄诗煌.化工原理优化设计与解题指南[M].北京:化学工业出版社,2001:79-113.

[5] 吴俊生,邵惠鹤.精馏设计、操作和控制[M].北京:中国石化出版社,1997:359-372.

[6] 单廷亮,胡仰栋,安维中,等.基于优化的反应精馏塔简捷设计[J].化学工程,2008,36(6):1-4.

[7] 李虎林,巨永林,李良君,等.低温精馏分离稳定同位素13C的模拟优化研究[J].原子能科学技术,2009,43(增刊):54-58.

[8] Li Hu-lin,Ju Yong-lin,Li Liang-jun,et al.Separation of isotope13C using high performance structured packing[J].Chemical Engineering&Processing:Process Intensification,2010,49(3):255-261.

[9] 潘丽军,陈锦权.试验设计与数据处理[M].南京:东南大学出版社,2008:165-191.