一类四自由度混联可重构主模块的全域静刚度预估

孙 涛，宋轶民，李永刚,2，董 罡

(1. 天津大学机械工程学院，天津 300072；2. 天津职业技术师范大学机械工程学院，天津 300222)

一类四自由度混联可重构主模块的全域静刚度预估

孙 涛1，宋轶民1，李永刚1,2，董 罡1

(1. 天津大学机械工程学院，天津 300072；2. 天津职业技术师范大学机械工程学院，天津 300222)

为满足国家飞机、汽车等零部件制造作业需求，提出了一种混联可重构机械手，与同体积的 Tricept机械手相比，该机械手能实现更大的工作空间，对其四自由度混联主模块的关键设计指标——静刚度进行了研究.考虑到主模块的拓扑构型为混联形式，将主模块划分为并联子系统和串联子系统.在利用虚功原理和子结构综合思想分别建立并联和串联子系统静刚度解析模型的基础上，借助线性叠加原理构造了球坐标系下主模块的整体静刚度解析模型.借助三维造型和有限元商用软件对主模块进行了建模和有限元分析，验证了该主模块整机静刚度解析模型的有效性，并结合算例对四自由度混联主模块的静刚度进行了全域预估.研究结果为研制具有我国自主知识产权的并/混联构型装备提供了理论依据.

混联可重构机械手；静刚度预估；子系统；虚功原理；有限元分析

可重构并联构型装备(reconfigurable parallel kinematic machines)是指为满足客户需求进而可快速改变其结构及软、硬件形式与功能的构型装备，由美国Michigan大学Koren教授提出的这一概念极大地促进了可重构构型装备的模块化发展，为制造业提供了更多选择[1].目前最成功的范例之一当属西班牙PKM Tricept公司生产的 Tricept[2]系列模块，该类模块具有速度高、刚度大、可重构性强等优点，已被制成高档数控机床或机器人，在波音、空中客车、大众、通用等大型飞机和汽车制造厂商进行了应用.Tricept机器人在工业上取得的巨大成功，引起了学术界的广泛关注，文献[3-7]对其运动学、精度、刚体动力学和静刚度问题进行了较深入的研究.

从机构拓扑构型的角度，Tricept机器人是由一个球坐标并联机构和1个二自由度(2-degree-offreedom，2-DoF)末端执行器组成，其中球坐标并联机构包含3条UP S支链和1条UP支链(U代表虎克铰链、S代表球铰链、P代表移动副、P 代表主动移动副).笔者在球坐标机构和2-DoF末端执行器之间加入了一个主动移动副P，构成了一个可重构机器人，包括1个4-DoF混联可重构主模块和1个2-DoF末端执行器.考虑此类构型装备主要应用在大型结构件加工、零部件装配和白车身焊接等领域，静刚度是其虚拟样机设计与开发的重要性能指标之一.国内外学者借助结构矩阵法和螺旋理论等工具[8-9]对一些经典并联机床的静刚度进行了分析，然而，与分析和设计工作主要集中在纯并联主模块上不同，对主模块为混联模块的研究相对匮乏.笔者首先将上述4-DoF混联主模块划分为并联和串联2个子系统，在分别建立2个子系统静刚度解析模型的基础上，利用线性叠加原理构建了4-DoF主模块的整体刚度模型，并利用有限元方法(finite element analysis，FEA)验证了其有效性，最后结合算例对其静刚度进行了工作空间中的全域预估，为其虚拟样机的设计和制造奠定了理论基础.

1 机构描述

如图1所示，新型可重构机器人由1个4-DoF混联可重构主模块和 1个 2-DoF末端执行器组成.为构造4-DoF主模块的整机静刚度模型，将其划分为并联子系统和串联子系统.并联子系统包括 1个静平台、1个动平台、3条无约束主动 UPS支链和 1条恰约束从动UP支链，而串联子系统则由1条主动P支链构成.3条 UP S支链的拓扑结构完全相同，一端通过虎克铰链与静平台相连，另一端通过球铰链与动平台相连接；UP支链一端通过虎克铰链与静平台相连，另一端则与动平台固接；主动 P 支链一端被包含在UP支链内，另一端与 2-DoF末端执行器固接，可相对于动平台末端移动，而2-DoF末端执行器是为了提高机器人的姿态能力.

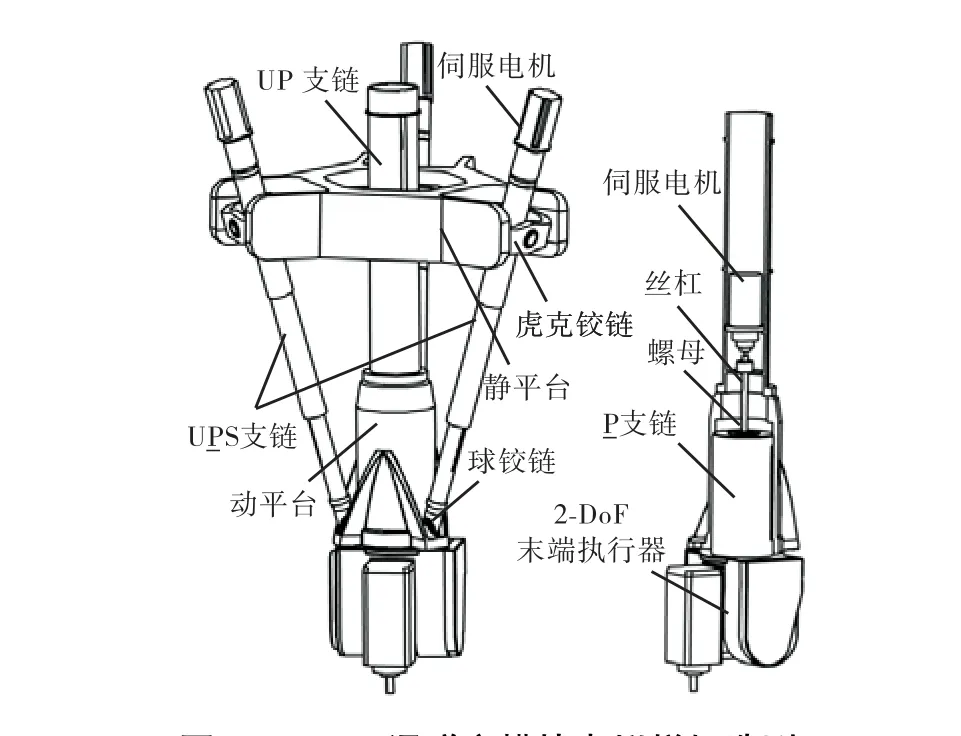
图1 4-DoF混联主模块虚拟样机造型Fig.1 Virtual prototype of 4-DoF hybrid module

图 2给出了 4-DoF混联主模块的结构示意.图中：点 Bi(i＝1，2，3)为 UPS支链 i的虎克铰链的中心；点Ai为其球铰链的中心；点O为UP支链虎克铰链的中心；点 A4和点 P分别为并联子系统和串联子系统的末端参考点.不失一般性，静平台和动平台平面为外接圆半径分别等于b和a的2个等边三角形平面.qi和 wi分别表示 UP S支链的长度和轴线的单位矢量，q4则表示并联和串联子系统的末端点之间的距离.在静平台平面内，以点O为原点建立固定坐标系Oxyz，其中x轴与UP支链虎克铰链外圈支承轴线重合，z轴与静平台平面垂直，而 y轴满足右手定则.为描述动平台姿态，以点A4为原点建立动坐标系A4uvw，其中 v轴与 UP支链虎克铰链内圈支承轴线重合，w轴与UP支链轴线重合并由点O指向点A4，u轴满足右手定则.

图2 4-DoF混联主模块结构示意Fig.2 Schematic diagram of 4-DoF module

根据上述定义，系 A4uvw相对系Oxyz的姿态可通过首先绕x轴旋转φ角，然后绕v轴旋转θ角来实现.据此，系A4uvw相对系Oxyz的姿态矩阵可表示为

式中wx、wy和wz是单位矢量w沿系Oxyz3个坐标轴的分量.

2 静刚度解析模型

不失一般性，在构造4-DoF混联主模块整体静刚度解析模型时，假定各零部件静变形均属线弹性小变形范畴.假定静、动平台均为理想刚体，各铰链所受约束均为理想约束，各轴承接触变形可忽略不计.基于上述假定，在分别考察并、串联子系统静刚度的基础上，构造了4-DoF混联主模块整体静刚度解析模型.

2.1 并联子系统静刚度解析模型

以下暂将串联子系统视为刚体，仅计因并联子系统弹性而引起的4-DoF混联主模块的末端变形.

假定作用于串联子系统末端参考点 P的6维载荷为FP，相应的6维变形为ΔP，由虚功原理得

式中τ和Δ分别表示并联子系统末端参考点A4的6维内力及相应的弹性变形.

式中 Kb和 K'b分别表示仅计并联子系统弹性时 4-DoF混联主模块及其并联子系统的静刚度矩阵.

考虑到串联子系统暂视为刚体，故下述变形映射成立

假定并联子系统各支链末端内力、变形及其静刚度矩阵分别表示为 f、Δq和 K'q，由虚功原理及虎克定律可得

并联子系统变形与其各支链末端变形的映射关系可表达为

式中：Ka和 Kc分别表示并联子系统的驱动和约束静刚度矩阵；kai表示第 i条 UPS支链的轴向刚度；Kcb表示 UP支链末端的等效弯曲刚度矩阵；kct表示 UP支链末端绕其轴向的扭转刚度.其中，Ka和 Kc的具体表达如下.

如图 3所示，由 UP S支链的具体机械机构及其力传递关系知

式中：kaij(j＝1，7)分别表示 UPS支链球铰链和虎克铰链沿支链轴向的刚度；kaij(j＝2～6)分别表示 UPS支链伸缩杆、螺母、丝杠、轴承的轴向刚度.

UP支链仅受扭转力时，由力的传递关系得

图3 UPS支链结构Fig.3 Schematic diagram of UPS limb

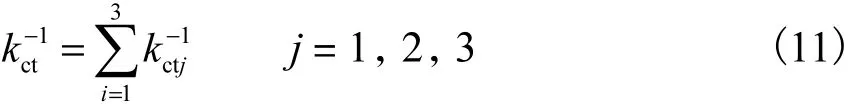
式中 kctj分别表示 UP支链套筒前段、后段及虎克铰链绕UP支链轴向的扭转刚度.

借助结构力学理论，将 UP支链处理成超单元[10]，其弯曲刚度矩阵为

式中K'e的具体表达可参见文献[10].

2.2 串联子系统静刚度解析模型

以下暂将并联子系统视为刚体，仅计因串联子系统弹性而引起的4-DoF混联主模块的末端变形.

假定作用于串联子系统末端参考点 P的6维载荷为FP，相应的6维变形为ΔP，由虚功原理得

式中，kPaj(j＝1，2，3，4)分别表示串联子系统的伸缩杆、螺母、丝杠和轴承的轴向刚度；kPaj(j＝5)表示 UP支链与电机端轴承固接部分到末端的轴向刚度.

考虑到串联子系统支链末端同时承受剪力、弯矩和扭矩，故将KPc写为分块矩阵形式

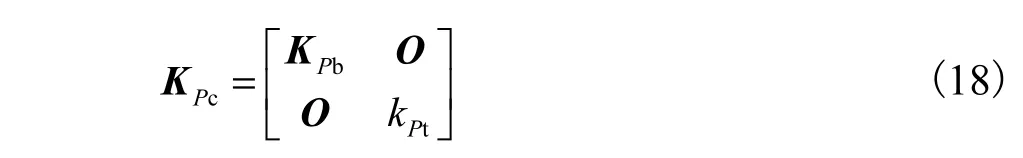
式中：kPt= G IP/q4表示串联子系统支链末端的扭转刚度；KPb表示串联子系统支链末端的弯曲刚度矩阵，利用超单元方法可得

式中，EI为P 支链伸出部分的抗弯截面模量.

图4 UP支链和P支链的结构Fig.4 Schematic diagram of UP and Plimbs

2.3 4-DoF主模块静刚度解析模型

借助线性叠加原理，可得在4-DoF主模块末端参考点P处的载荷作用下，主模块静刚度矩阵为

式中K表示4-DoF混联主模块的整机静刚度矩阵.

为便于观察整机静刚度的分布情况，可将 K转化至如图 5所示的球坐标系 Pu''v''w''下.其中，w''轴与 UP支链轴线重合，v''、w''轴分别与进动角 ψ、章动角θ的正向一致.

图5 4-DoF主模块球坐标系Fig.5 Spherical coordinate system of 4-DoF module

3 静刚度解析模型验证

假定4-DoF混联主模块的工作空间为一半径1,000,mm、高 300,mm 的圆柱体，借助尺度综合可得该主模块的其他尺度参数，进而可利用商用三维造型软件构造该4-DoF混联可重构主模块的物理样机模型，如图1所示.在此基础上，利用商用有限元软件可建立4-DoF混联主模块的有限元模型，考虑到商用有限元软件ANSYS仅能解决离散位姿的静刚度预估问题，为验证静刚度解析模型的有效性，可针对工作空间中的典型位姿Ⅰ和Ⅱ(见图 6)，构造其虚拟样机的有限元模型，并求其末端的各向刚度.同时，表1～表3给出了4-DoF主模块各零部件的刚度参数值.

图6 工作空间中的典型位姿Fig.6 Point position in workspace

表1 UPS支链线刚度Tab.1 Axial stiffness of UPS limb

表2 UP支链角刚度Tab.2 Torsional stiffness of UP limb

表3 P支链线刚度Tab.3 Axial stiffness of Plimb

根据上述 4-DoF混联可重构主模块的静刚度解析模型和有限元模型，可得在其工作空间中2个典型位姿处的解析模型和有限元模型的计算结果，如表 4所示.在未计入静/动平台弹性和忽略轴承接触变形的前提下，解析模型和有限元模型的计算结果已比较接近，两者的最大差值小于 13%，因此上述所建立的4-DoF混联主模块的整机静刚度解析模型是有效的，可用于后续的灵敏度分析、静刚度预估和设计等.

表4 解析模型与有限元模型计算结果比较Tab.4 Comparison of analytical and FEA models result

4 静刚度全域预估

本文所建立的4-DoF混联主模块的整机静刚度解析模型已经借助有限元方法验证了其有效性，利用表 1～表 3中的各零部件的刚度参数值，在球坐标系Pu''v''w''下，借助数值算法可得4-DoF主模块工作空间上中下3个平面上的静刚度分别情况，如图7所示.图中：kpφ、kpθ、kpr分别表示 u''向、v''向、w''向的线刚度；kαφ、kαθ、kαr分别表示绕u''向、v''向、w''向的角刚度.

如图7所示，4-DoF混联主模块末端的各向刚度均呈近似三对称分布，且均在 z轴取得最大值；kpr与kαr的分布规律近似，且均随章动角 θ的增大而单调递减；在工作平面的边缘处，kpφ与 kαφ(kpθ与 kαθ)的分布规律相反，若前者取得极小值则后者取得极大值，反之亦然；此外，工作平面距静平台平面的距离愈小，其对应的线(角)刚度分布曲面的位置“愈高”.换言之，UP/P 支链伸长量愈小，整机静刚度性能愈好.

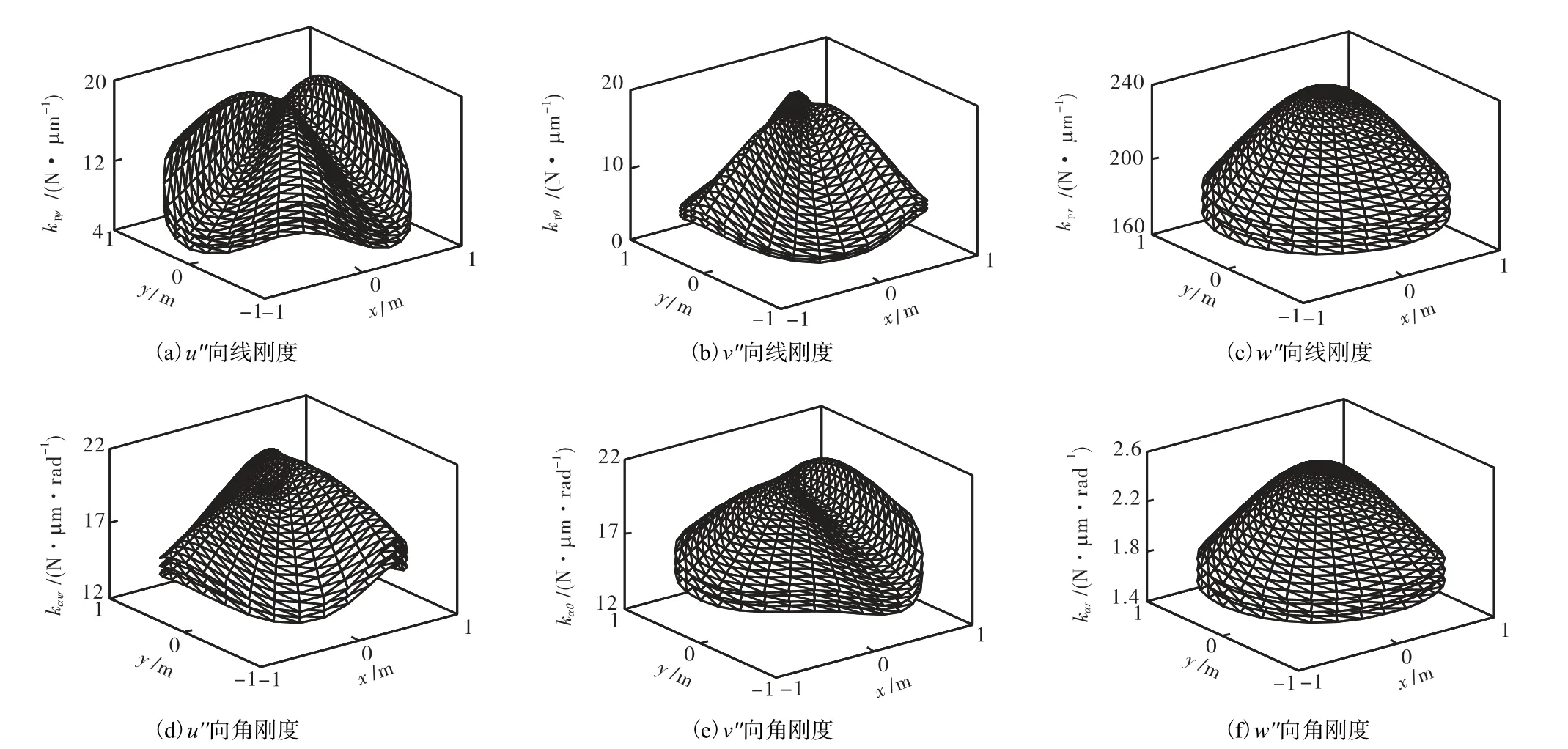
图7 4-DoF混联主模块静刚度在工作空间上中下3个平面的分布Fig.7 Stiffness distribution of 4-DoF module over upper, middle and bottom planes in workspace

利用相同的方法可求得 4-DoF混联主模块工作空间中的任意一点的静刚度值，从而完成其在工作空间中的全域刚度预估，为4-DoF混联主模块的虚拟样机的设计奠定理论基础.

5 结 论

面向国家飞机、汽车等零部件制造需求，对一类4-DoF混联主模块的全域静刚度预估问题进行了研究，为研制具有我国自主知识产权的并/混联构型装备提供了理论依据.结论如下：

(1) 考虑到4-DoF主模块的混联特性，借助子结构综合的思想，分别建立了其并联和串联子系统的静刚度模型，进而利用线性叠加原理得到了4-DoF混联主模块的整机静刚度模型.

(2) 借助商用三维造型和有限元软件，构建了4-DoF主模块工作空间中典型位姿的虚拟样机模型，进行了有限元分析，并将其结果与解析模型的结果进行了比照，两者最大差值小于 13%，验证了整机静刚度解析模型的有效性.

(3) 利用经过验证的整机静刚度解析模型，借助数值算法得到了4-DoF主模块工作空间上中下3平面的刚度分布情况，揭示了其分布规律.

［1］Koren Y，Heisel U，Jovane F. Reconfigurable manufacturing systems[J].Annals of the CIRP，1999，48(2)：527-540.

［2］Neumann K E. Robot：US，4732525[P]. 1998.

［3］Zhang Yanbin，Liu Hongzhao，Wu Xin. Kinematics analysis of a novel parallel manipulator[J].Mechanism and Machine Theory，2009，44(9)：1648-1657.

［4］Sun Tao，Song Yimin，Li Yonggang，et al. Dimensional synthesis of a 3-DOF parallel manipulator based on dimensionally homogeneous Jacobian matrix[J].Science China Technological Sciences，2010，53(1)：168-174.

［5］Sébastien B，Ilian A B. Accuracy analysis of 3T1R fullyparallel robots[J].Mechanism and Machine Theory，2010，45(5)：695-706.

［6］Altuzarra O，Zubizarreta A，Cabanes I，et al. Dynamics of a four degrees-of-freedom parallel manipulator with parallelogram joints[J].Mechatronics，2009，19(8)：1269-1279.

［7］Li Yangmin，Xu Qingsong. Stiffness analysis for a 3-PUU parallel kinematic machine[J].Mechanism and Machine Theory，2008，43(2)：186-200.

［8］Zhang Dan. On stiffness improvement of the Tricept machine tool[J].Robotica，2005，23(3)：377-386.

［9］Xu Qingsong，Li Yangmin. An investigation on mobility and stiffness of a 3-DoF translational parallel manipulator via screw theory[J].Robotics and Computer Integrated Manufacturing，2008，24(3)：402-414.

［10］Wang Youyu，Huang Tian，Zhao Xueman，et al. Finite element analysis and comparison of two hybrid robots—the Tricept and the Trivariant[C]//Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems.Beijing，China，2006：490-495.

Global Stiffness Estimation of 4-DoF Hybrid and Reconfigurable Module

SUN Tao1，SONG Yi-min1，LI Yong-gang1,2，DONG Gang1
(1. School of Mechanical Engineering，Tianjin University，Tianjin 300072，China；2. School of Mechanical Engineering，Tianjin University of Technology and Education，Tianjin 300222，China)

In this paper a hybrid and reconfigurable robot is presented in order to meet the demands of the component manufacture of aeroplanes and automobiles. Compared with the well-known Tricept robot, the unique topology of this robot leads to larger workspace. To ensure better performance of the virtual prototype design, an analytical approach is presented for evaluating the stiffness distribution throughout the workspace. The 4-degree-of-freedom (4-DoF) hybrid and reconfigurable main module in this novel robot is firstly decomposed into parallel and serial subsystems, after developing the stiffness analytical model of each subsystem based upon the principle of virtual work and the substructure synthesis method respectively. The stiffness model of the entire system in the spherical coordinate system is then formulated with resort to the linear superposition principle, whose validity can be further proved by 3D modeling and finite element analysis (FEA) software. Finally, the stiffness distribution of the 4-DoF main module may be investigated over the global workspace. The results mentioned above lay the theoretical basis for the design and manufacture of parallel/hybrid mechanism with Chinese intellectual property rights.

hybrid and reconfigurable robot；stiffness estimation；subsystem；virtual work principle；finite element analysis

TP241

A

0493-2137(2010)11-1003-06

2009-09-15；

2010-03-12.

国家自然科学基金资助项目(50675151，51075295)；国家高技术研究发展计划(863计划)重点资助项目（2007AA042001)；教育部博士点基金资助项目（20060056018）.

孙 涛（1983— ），男，博士研究生，suntaotju@gmail.com.

宋轶民，ymsong@tju.edu.cn.