两个连通球形液膜有平衡状态

李咏梅

(济宁学院物理系,山东 曲阜 273155)

近年来,出现了不少关于连通肥皂泡或是球形液膜(以下简称液泡,如肥皂泡)动态特性的讨论[1-4].有些研究认为,当大小不同的两个液泡连通后,小泡不断缩小,大泡不断增大,当小泡缩小到半球面形状后,还要继续缩小,但这时曲率半径反而增大,当它和大泡曲率半径相同时便趋于稳定[3,4].有些研究直接基于这一理论,对连通后大小泡的变化进行模拟与阐释[1,2].笔者认为这些讨论不够深入,这里拟对此进行深入的讨论,并计算两球形液膜的动态和平衡态,同时研究气体传输过程中液泡的动态规律,对于区分理解两个大小不同的连通肺泡在人体呼吸过程中的变化特性具有一定的参考价值[4].

图1

1 两个球形液膜理论推导

球形液膜由于受液体表面张力的作用,导致液泡内外气体压强间存在一定的压强差,该压强差通常称为附加压强,其大小为其中α为液体表面张力系数,r为球形液泡的半径[5].如图1,用细短管连通A、B两大小不等的液泡,设其初态半径为R1、R2,液泡内气体质量为m10、m20,液体表面张力系数为α.由于附加压强的缘故,A内压强大于B内压强,气体将从小液泡A流向大液泡B.设其动态半径为r1、r2,液泡内气体质量为m1、m2.因液泡内压强接近大气压强p0,温度是常温,故可按理想气体处理.由于A、B两液泡间的细短管内径很小,液泡的动态压强可近似满足体积分别为将其分别代入理想气体状态方程中,可得动态气体状态方程

(1)、(2)式中,μ为摩尔质量,R为气体普适恒量,T为气体的热力学温度.将气体传输过程视为等温过程,则初态气体状态方程为

因系统在动态过程中质量守恒,则由(1)～(4)式可得

得动态半径r1与r2的近似函数式为

设细短管截面积为S,则气体沿管道等温流动时,单位时间A泡内气体流到B泡内的分子数为

单位时间B泡内气体通过细短管流到A泡内的分子数为

其中M是一个气体分子的质量.将(8)、(9)式代入(10)式得

由(1)式微分可得,在时间dt内,A液泡内气体的质量变化量为

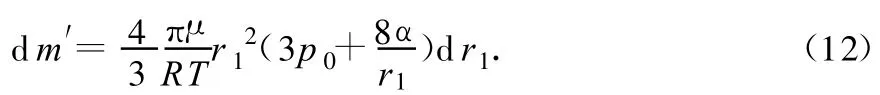
显然dm=-dm′,即有

但此反应脂肪酸中的不饱和双键也会发生氢化反应，常用该反应将植物油氢化为长链的脂肪醇，若要避免此类还原反应的发生，可用铜、镉的氧化物或其皂盐催化。

将(7)式代入(14)式,两边积分可得

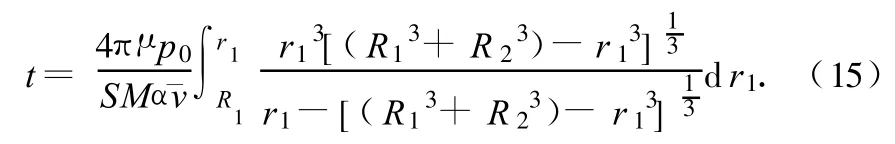
其中积分下限R1和上限r1分别为液泡A的初态半径和动态半径.

同理也可得时间t与液泡B的半径r2的关系式

其中积分下限R2和上限r2分别为液泡B的初态半径和动态半径.

则T(r1)、T(r2)就可以反应大小泡的动态变化情况.

2 液泡A收缩到球冠形的理论推导

液泡A的半径r1与细管的半径R0相当时,此时液泡A就不能看成球形,而应是球冠形,如图2所示(图2(a)为球冠形与球形液泡连通模型图,图2(b)为液泡A几何关系放大图).其中球冠半径为r1,冠高h,冠底半径等于管子半径R0,液泡B仍为球形,半径为r2.

图2

同理由(1)、(2)、(19)、(20)式可得

由图2(b)的几何关系知

同理由(10)～(12)式得

将(21)、(22)式代入(23)式,两边积分可得液泡A变化时间为

同理也可得液泡B的变化时间t与h的关系式仍为(24)式.

图3

图4

图5

因r1、r2与h存在关系式(21)、(22),可作T(r1)、T(r2)关系曲线反应大小泡的动态变化情况.由于T(r1)、T(r2)为不可积函数,可取球形液膜初态半径R1=25mm、R2=30mm、R0=2mm,利用Matlab7.0做数值积分并绘图,进行定性分析,得到T(r1)、T(r2)理论曲线如图3所示.液泡A变成球冠形后T(r1)理论曲线如图4所示.液泡A变成球冠形后T(r2)理论曲线如图5所示.

4 分析与讨论

(1)从图3曲线可见,在小液泡A从r1=25mm萎缩到r1=20mm的初始阶段,T(r1)随r1的减小快速增大;当r1减小到15mm后,T(r1)随r1的减小很缓慢地增大.具体解释见参考文献[2].

(2)当r1=R0以后,液泡A是球冠,r1的变化如图4,T(r1)随r1由小变大,且到r1=34.87mm时T(r1)变大r1=34.93mm保持一个定值.r2的变化如图5,T(r2)随r2变大而变大,且到r2=34.93mm时T(r2)变大r2=34.93保持一个定值,在图3上交于一点,此时就是平衡状态.

综上所述,我们可以得到如下结论:当大小不同的两个液泡连通后,由于较小的泡内的附加压强较大,气体就会被压入大泡,因此小泡不断缩小,大泡不断增大.随着小泡的不断缩小,其表面张力不断变大,它将加速萎缩.随着大泡不断增大,其表面张力不断变小,当达到一定时刻,它将有可能发生破裂.因此,两液泡能否变到曲率半径相同的稳定状态,是由表面张力系数,原初始状等外界条件决定.

5 结论

本文讨论了表面张力系数相同的液体构成的两球形液膜连通的动态特性,得到两液泡连通后,小泡不断缩小,大泡不断增大;两液泡变到曲率半径相同的稳定状态是在大液泡不发生破裂时才成立.由附加压强公式我们可以推论,若是表面张力系数分别为α1、α2(α1≠α2)的液体构成的半径分别为r1、r2(r1≠r2)的液泡,满足条件则产生相同的附加压强.也就是说表面活性物质浓度不同的液泡相连通,若的值相同,则将会保持平衡,这也正是肺泡的工作原理[6].

1 唐玄之,王琦等.大小肥皂泡连通后的讨论与计算.大学物理,2007,26(10):20-23

2 王云创,李德尧等.两个连通型球形液膜动态特性的研究.大学物理,2004,23(5):33-36

3 薛万华,刘月成等.物理化学简明教程.北京:地震出版社,2001.305

4 周衍椒,张镜如.生理学.北京:人民卫生出版社,1989.188-229

5 黄淑清,聂宜如等.热学教程(第2版).北京:高等教育出版社,1994.255,343

6 王玢,左明雪.人体及动物生理学(第2版).北京:高等教育出版社,2001.250