线性-非线性混合的约束模态综合法及实践

姜忻良，王 菲

(天津大学建筑工程学院，天津 300072)

动态子结构法是近年来对大型复杂结构进行数值分析的常用方法．它通过将整体结构划分为多个子结构，再充分利用各子结构的动态特性最大限度地缩减自由度数，以简便计算过程，最终获得可靠的原系统动力特性参数或动态响应[1]，无疑是大型复杂结构进行地震响应分析的有效方法．动态子结构法按照子结构连接方式的不同，可以分为约束模态综合法[2-3]、自由界面模态综合法[4]和混合界面模态综合法等．其中，约束模态综合法由于概念清晰，易于理解，不会出现悬浮子结构[5]，并且计算过程中自由度较少，具有较高的计算效率，因此，应用较为广泛．然而，从理论上讲，动态子结构法仅适合于求解线性结构系统的动力问题，这就使得动态子结构法对于非线性结构体系的进一步应用受到了限制．

经研究发现[5]，在许多实际工程中，整体结构在荷载作用下，并非全部构件都进入非线性阶段，而是仅仅在某些位置才出现非线性特征，这就说明了结构存在局部塑性区域的特点．例如桥墩在地震作用下，墩底首先进入非线性阶段；悬臂梁在自由端作用一竖向荷载后，固定端会很快出现非线性特征直至破坏等等．而这其中，土与结构相互作用问题也是一个典型的例子，在地震响应分析问题中，仅仅与上部结构邻近的地基土区域会产生塑性应变，出现非线性特征，而远离上部结构的地基土区域在整个加载过程中却始终处于线性阶段．据此若能将局部非线性区域单独划分子结构，并与缩减后的线性子结构综合，将会更大程度上缩减非线性体系的自由度，降低计算本．

基于上述考虑，笔者提出了线性-非线性混合的约束模态综合法，并在理论上论证了该方法的可行性．此外，还提出了基于势能判据的子结构主模态的截断准则，利用势能判据的收敛性得出了子结构主模态最佳截断阶数．最后将线性-非线性混合的约束模态综合法以及基于势能判据的截断准则应用到高层建筑-地基土非线性地震响应分析问题中，并与有限元直接法进行了对比分析，以验证所提出方法的有效性．

1 线性-非线性混合的约束模态综合法

对于非线性结构的动力分析问题，若以局部非线性来代替整体结构的非线性，而对局部非线性以外的线性部分采用约束模态综合法，那么首先就需要证明约束模态综合法是否能够解决仅对线性子结构进行自由度的缩减，而对其余非线性子结构不进行缩减的混合问题，即能否同时在物理坐标和广义坐标下进行综合求解的问题．为了论证这一线性-非线性混合的约束模态综合法在原理上的正确性和可行性，下面以一个悬臂梁(见图1)为例，来进行公式推导．

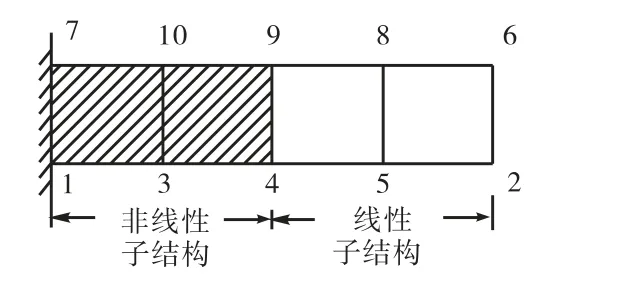
图1 悬臂梁示意Fig.1 Diagram of cantilever beam

该悬臂梁由4个单元组成，分为2个子结构：靠近固端的非线性子结构(子结构 1)和自由端的线性子结构(子结构 2)．对于非线性子结构，不做自由度的缩减，而直接采用物理坐标来表示其运动方程，即

将非线性子结构的质量矩阵、阻尼矩阵、刚度矩阵和荷载矩阵按照内部节点(用 I表示)和边界节点(用 B表示)的形式分块表示，则式(1)写为

式(3)即为非线性子结构在物理坐标下的运动方程．

对于线性子结构，可用约束模态综合法进行自由度的缩减，同样将其特性矩阵、荷载矩阵和位移向量等按照内部节点和边界节点进行分块处理，则有

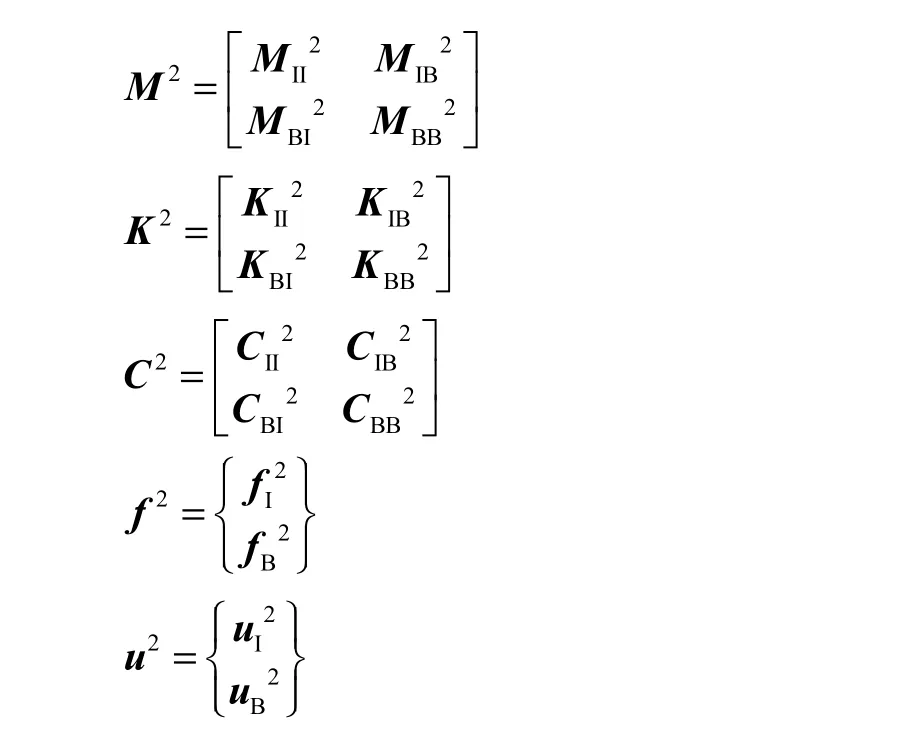
约束模态综合法的子结构坐标变换矩阵由 2部分组成，一是边界约束的子结构主模态矩阵KΦ；二是约束模态矩阵CΦ[6]，且有

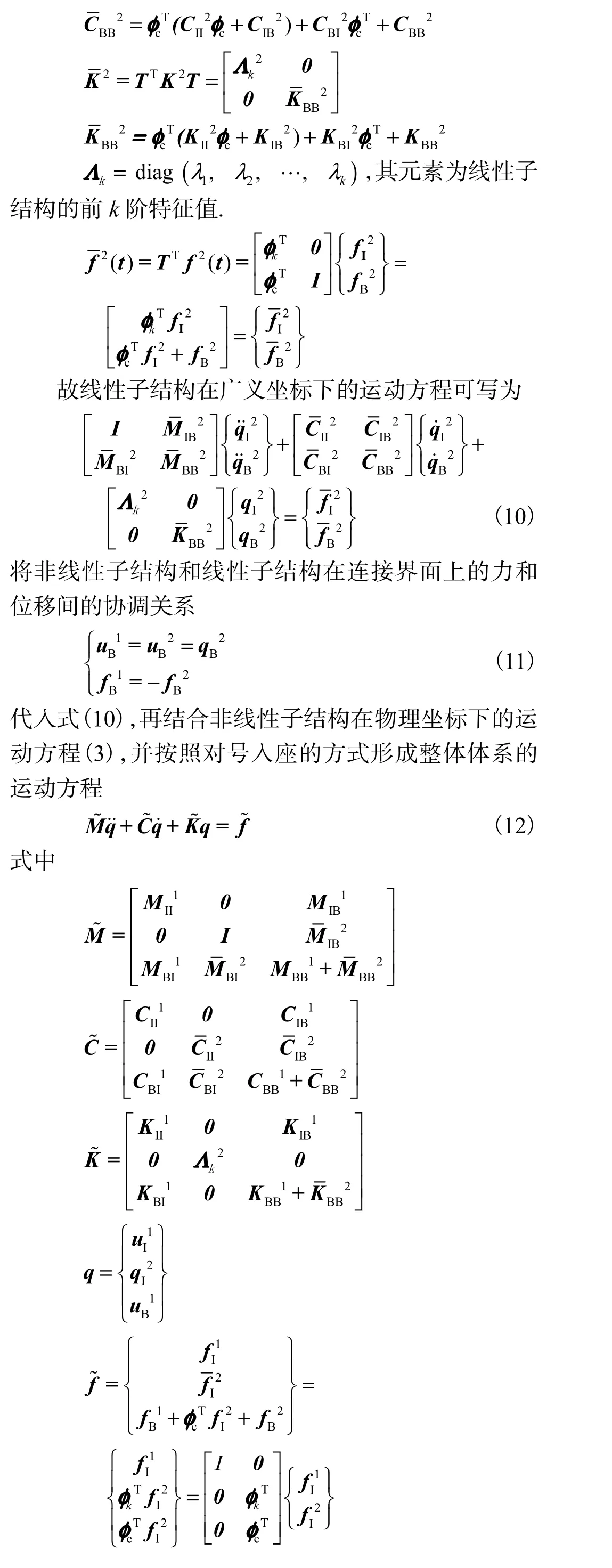
对于综合后含有非线性子结构的非线性运动方程(12)，只需采用常用的非线性方程求解方法(如Newmark-β法、Wilson-θ法等)，即可得到体系的动力响应，求得的位移响应中既包括线性子结构在广义坐标下的位移解也包括非线性子结构在物理坐标下的位移解，即通过式(14)，即可返回各子结构在物理坐标下表示的位移解

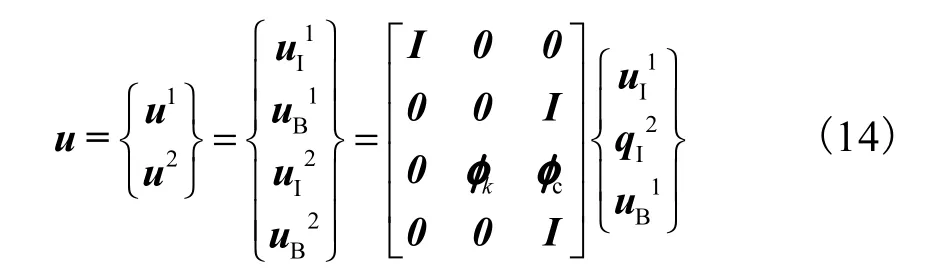
由上述推导可见，线性-非线性混合的约束模态综合法在理论上是合理可行的，它将原本不易进入非线性阶段的部分划分成线性子结构进行自由度缩减，而不必在整体非线性模型中反复进行迭代计算，最终通过与非线性子结构的综合来求解整体非线性方程，这样就可以极小的计算成本，获得非线性体系的动力解，极大程度地降低了计算成本、提高了计算效率．

2 基于势能判据的截断准则

在上述求解过程中，对于线性子结构，一个突出的问题就是如何从完备的子结构主模态nφ(n为完备的子结构模态总阶数)中截取kφ(kn＜)用以形成坐标变换矩阵，使得既能大幅度的缩减自由度，又能尽量减小因丢弃高阶模态所引起的截断误差．很多文献针对这一问题提出了模态截断准则，然而，这些模态截断准则往往存在不确定性．有些准则依靠经验来确立，但随着研究对象的不同，会给计算结果带来误差；有些则依靠基本的动力学理论来确立，大都需要一定试算后才可确定截断数量．因此，寻找有效的截断准则仍是迫切需要解决的问题，本文根据势能判据提出了一种新的模态截断准则．

3 高层建筑-地基土非线性地震响应分析

在高层建筑-地基土非线性地震响应分析问题中，土体是半无限系统，在利用有限元分析时，需要将半无限空间的土体有限化，当有限化的土体取到一定范围时，可以忽略侧向入射波和散射波的影响[10]．但是，当考虑了土体的非线性特性时，有限元计算也会带来庞大的计算量．然而研究表明，在地震作用下，仅与建筑物邻近的地基土会随着加载而逐渐进入非线性阶段，而远离建筑物的土体区域仍会保持线性特征．这样，就可以根据经验划分出非线性区域，采用线性-非线性混合的约束模态综合法，来达到降低计算成本的目的．

以一个15层三跨框架结构为例，分别采用线性-非线性混合的约束模态综合法和有限元直接法进行非线性动力时程分析．该框架层高3.2,m，跨度6,m．柱截面尺寸为 600,mm×600,mm，梁截面为300,mm×600,mm，各层楼面质量 19,600,kg．承台高2,m，宽 18,m，E = 3.25× 1 010N/m2．土体区域沿承台两侧宽度各取 91,m，沿深度方向取 40,m．地基土地质参数见表 1．在水平方向输入地面波，采用天津地区地震动加速度时程曲线，如图 2所示，采样频率为0.02,s，地震动加速度峰值为3.10 m/s2．

表1 地基土地质参数Tab.1 Geologic parameters of soil

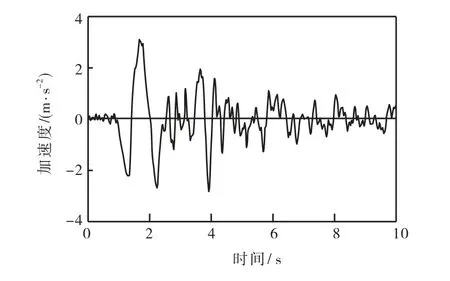
图2 输入地震动加速度时程Fig.2 Time history acceleration of earthquake ground motion

采用线性-非线性混合的约束模态法分析过程中，计算模型的子结构划分方法如图 3所示，与框架结构相邻的地基土为非线性子结构．在计算中，对非线性子结构直接引入非线性 DP本构模型，按照非线性模式进行求解．而对于周围土体区域则应采用线性本构模型．对于非线性区域的划分，经过试算，可取计算区域中心至人工边界的距离为 5倍的非线性土层深度，且计算区域中心至非线性区域边界的宽度与其土层深度之比大于 1.5[10]．经过试算可以确定，对于上述算例，承台中心至人工边界取可为 100,m，承台中心位置至非线性区域的边界的宽度 D可取为60,m，非线性土体深度H可取为23.5,m．

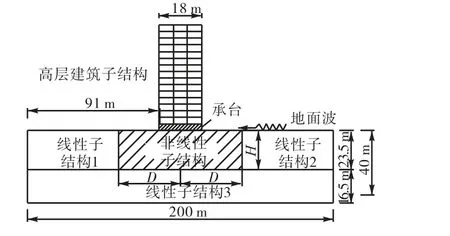
图3 子结构示意Fig.3 Diagram of substructure

按照线性-非线性混合的约束模态综合法的基本原理，需对线性子结构进行缩减，采用基于势能判据的截断准则，可得到各个线性子结构的势能随截取主模态阶数的变化曲线，如图 4所示．由此可确定，线性子结构 1、2、3分别需截取其各自主模态的前 48、48和108阶投入综合．

计算得到的框架顶层位移、速度、加速度时程曲线，以及最大层间位移时程曲线如图 5所示．从图中可以看出，考虑局部非线性后所得的结果与未作该假定时的结果之间的相对误差很小．2种方法得到的结果曲线基本吻合，然而采用线性-非线性混合的约束模态综合法后却节省了大量机时，2种方法(均采用Intel 3.20 GHz，16 GB内存的计算站进行计算)所消耗的计算时间对比如表 2所示．可以看出，它仅以直接法耗时的 0.66%就达到了与其同样的计算精度，无疑是解决非线性土-结相互作用问题的有效手段．

图 6给出了采用有限元直接法计算得到的塑性应变云图，可以清晰地看出，仅框架结构下方的土体进入了非线性阶段，产生了塑性应变，而远离建筑物的周围土体仍然保持在线性阶段．因此进一步证明了采用本文所提出的线性-非线性混合的约束模态综合法是合理、有效的．

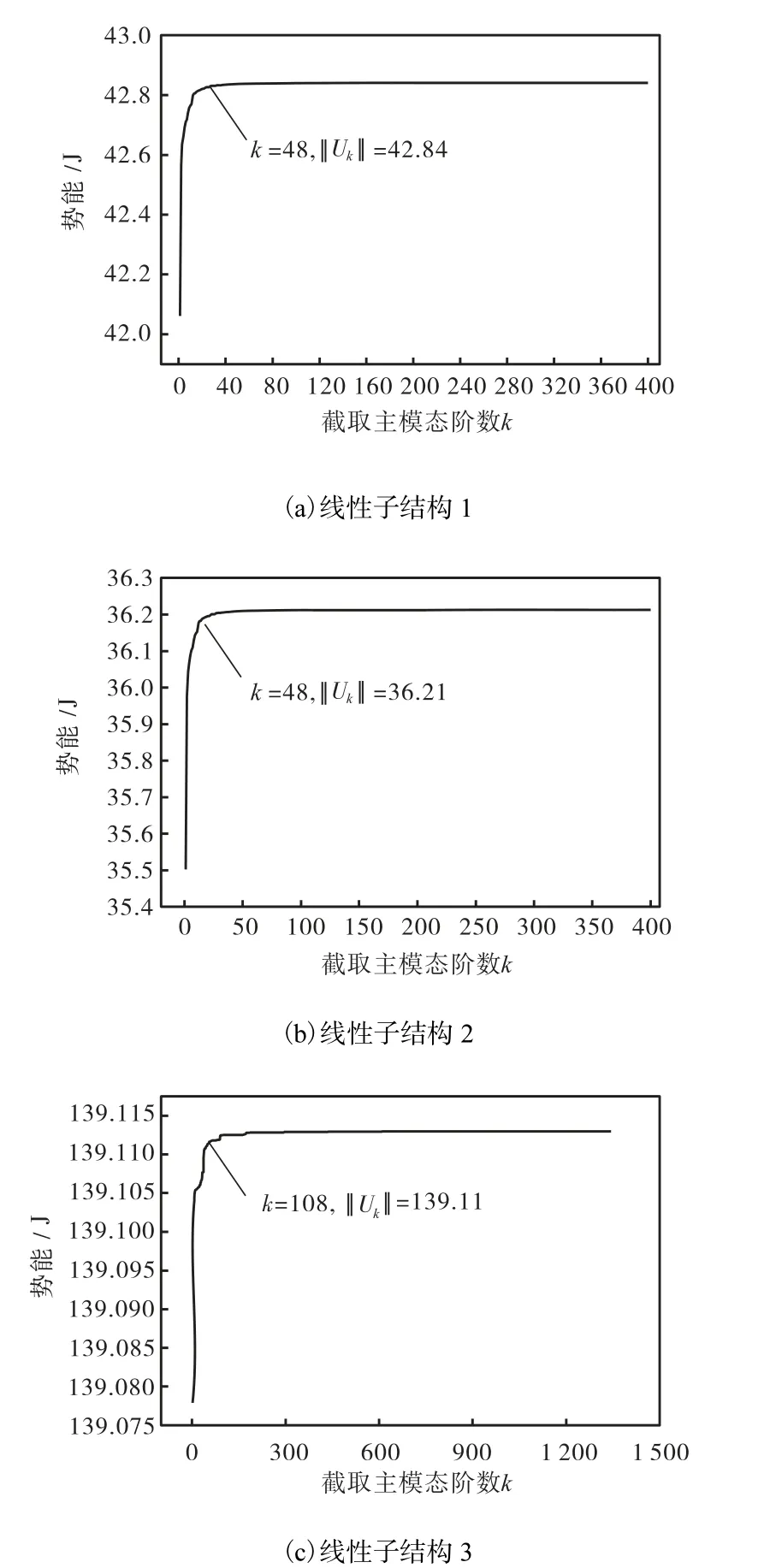
图4 势能随截取主模态阶数的变化曲线Fig.4 Variation of potential energy with mode cutoff number

图5 框架地震响应时程曲线Fig.5 Time history curves of displacement，velocity and acceleration of frame

表2 计算效率对比Tab.2 Comparison of computational efficiency

图6 塑性应变云图Fig.6 Plastic strain contour plot

5 结 论

(1)本文根据结构存在局部塑性区域的特点，提出了线性-非线性混合的约束模态综合法．即将整体体系中未进入非线性阶段的部件，将其划分为线性子结构，而将进入塑性变形阶段的局部部件独立划分为非线性子结构，通过坐标变换来缩减线性子结构的自由度，并最终与非线性子结构进行综合求解，使动力子结构方法得以扩充，在降低计算成本的同时，又能够合理的对结构的材料非线性特征加以考虑，为求解大型复杂结构非线性动力问题开辟了新的途径．

(2)针对约束模态综合法，定义了由不同主模态截断阶数产生的位移向量组成的线性空间，建立了该空间上的范数，并以该范数的最大值定义势能判据，据此提出了一种基于势能判据的子结构主模态截断准则——势能判据截断准则，计算表明截断准则适用于线性-非线性混合的约束模态综合法．

(3)通过高层建筑-地基土相互作用的地震响应分析算例，进一步验证了本文所提出的线性-非线性混合的约束模态综合法的可行性与精确性．

［1］ 楼梦麟. 结构动力分析的子结构方法[M]. 上海：同济大学出版社，1997.

Lou Menglin.Substructure Methods of Structural Dynamic Analysis[M]. Shanghai：Tongji University Press，1997(in Chinese).

［2］ Tran D M. Dynamic analysis of structural systems using component mode[J]. Computers and Structures，2001，79：209-222.

［3］ Craig R R J. A review of time-domain and frequencydomain component mode synthesis method[J]..Int JAnalytical Exp Modal Analysis，1987，2(2)：59-72.

［4］ Bucher C U A. A modal synthesis method employing physical coordinates，free component modes and residual flexibilities[J]. Computers and Structures，1986，22(4)：559-564.

［5］ 白建方. 复杂场地土层地震反应分析的并行有限元方法[D]. 上海：同济大学土木工程学院，2007.

Bai Jianfang. Parallel Finite Element Method for Seismic Response Analysis of Irregular Site[D]. Shanghai：College of Civil Engineering，Tongji University，2007(in Chinese).

［6］ Craig R R Jr，Chang C J. A review of substructure coupling methods for dynamic analysis [J]. Advances in Engineering Science，1976，2(2)：393-408.

［7］ Wamsler M. On the selection of the mode cut-off number in component mode reduction[J].Engineering with Computers，2009，25：139-146.

［8］ Craig R R Jr. Substructure method in vibration[J].Journal of Mechanical Design，1995，117(B)：207-213.

［9］ 熊洪允，曾绍标，毛云英. 应用数学基础[M]. 天津：天津大学出版社，2004.Xiong Hongyun，Zeng Shaobiao，Mao Yunying.Applied Mathematics[M]. Tianjin：Tianjin University Press，2004(in Chinese).

［10］ 白建方，楼梦麟. 基于动力子结构方法的场地地震反应分析方法[J]. 震灾防御技术，2008，3(2)：145-154.

Bai Jianfang，Lou Menglin. The dynamic substructure method for seismic response of irregular topography[J].Technology for Earthquake Disaster Prevention，2008，3(2)：145-154(in Chinese).