高速电机高精度伺服控制

郝双晖，唐梓力，郝明晖，刘 杰

(哈尔滨工业大学机电工程学院，哈尔滨 150001)

高速电机越来越广泛地应用于工业、军事等领域．用高速电机直接驱动负载，可省去变速装置，降低机械振动与噪声，提高运行效率和运行精度，减小设备体积[1-2]．目前高速电机的驱动方式主要采用变频调速和无位置传感器的直接转矩控制．高速电机的高精度伺服控制技术发展缓慢．其主要原因在于，高速下很难实现对转子位置的精确检测[3-4]．

高速下的转子位置检测技术是伺服系统向高速高精度方向发展的一个必要条件．电机转子位置的检测通常有 2种方式：一种是无传感器方式(如基于状态观测的逼近算法)；另一种是利用位置传感器(如光电编码器、磁电编码器、同步感应器等)．无位置传感的控制方式是目前伺服电机控制研究的热点，它在提高系统可靠性、提高高速阶段控制性能等方面有一定的优势，但目前单一的无传感器矢量控制方法还不能够实现从零速启动等其他基本动作的控制，因此无法在整个速度范围内准确地控制电机运行[5-7]，不能用于精确的位置控制．对于后者，传感器结构、敏感元件响应时间等方面的局限使其在高速场合的应用受到制约．以光电编码器为例，高精度伺服控制通常要求编码器分辨率为14～16位，则在如此高精度的伺服控制中，要使电机转速达到 10,000,r/min以上，则要求光敏元件带宽达到 2,MHz以上[8-10]．高响应频率的光敏元件价格极其昂贵，而如此高的响应频率甚至超出了当前传感器行业的技术能力．此外光电编码器均采用实时的位置反馈方式，在高转速时反馈信号频率过高，通信可靠性很难保证[11]．多极磁电编码器也存在同样的问题．

综上可见，在目前位置检测方法下，高伺服精度和高转速不可兼得．针对此问题，笔者提出一种单极式磁电编码器的设计，此编码器可在较高转速下反馈16位分辨率的转子位置信号，采用定时滞后的位置反馈方式，用同步串口以一定的时间间隔和固定通信频率上报绝对角度，通信可靠性高．在此基础上，笔者提出了基于此编码器的位置反馈滞后补偿方法和高速永磁同步电机的矢量控制方法．仿真和实验结果表明，此方法成功实现了对高速电机的伺服控制．

1 单极磁电编码器设计

1.1 设计要求

高速矢量控制要求编码器具有以下特点．

(1)在高转速下能正常检测和输出转子角度．不能采用光电编码器实时反馈的方式．

(2)旋转部件转动惯量小，材料强度较高，耐振动．为避免高速旋转时的摩擦，转子和定子之间最好完全无接触．

(3)电机能够高精度定位，要求编码器有较高的分辨率和精度．

1.2 组成和信号

基于以上要求，本文提出的磁电式编码器结构如图1所示．

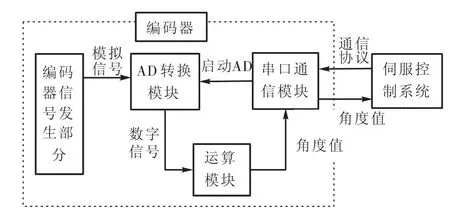
图1 编码器组成和信号传输Fig.1 Structure and signal transmission of encoder

编码器由信号发生部分和信号处理部分组成，信号发生部分是通过磁电效应原理产生能够反映跟轴一起转动的磁场方向的多相电压信号；信号处理部分对电压信号进行分析，根据多相电压信号与磁场位置的对应关系，得到轴(磁场)在一周内的绝对位置，在伺服控制系统触发通信时，上报电机轴位置信息．其中通信部分采用同步串行通信．

1.3 编码器工作原理及信号处理方式

单对极磁电式编码器信号发生部分如图2所示，主要由永磁体(转子)和磁敏元件(定子)组成．永磁体只有一对磁极，是由强磁材料钕铁硼制成的磁钢环，固定在电机尾轴上，用半导体霍尔元件作磁敏元件，装在电机尾部端盖上，这样就借用电机定、转子运动副，实现了编码器定子、转子精确而又无接触地相对运动．永磁体旋转一圈，磁场变化一周期，每组磁敏元件输出一个周期的电压信号，在一周内，任意转子(永磁体)位置(0°～360°)与多相电压信号组合唯一对应．可见，在感应器件响应频率相同的条件下，相对于光电编码器一周内感应多周期(等于分辨率)信号的工作方式，这种方式可在更高转速下有效反馈转子位置．

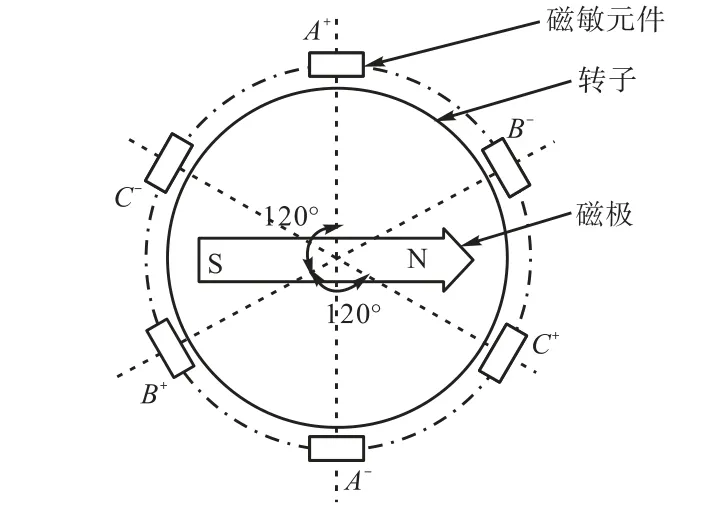
图2 编码器信号发生部分Fig.2 Signal generating unit of encoder

为保证编码器的精度，设计采用三相信号来进行角度判断．3组6个霍尔元件，在圆周上均匀分布，相位差 180°的2个构成一组，每组元件的输出信号经差分后作为一相信号，这样可以消除零点飘移、共模噪声以及机械安装误差等带来的信号误差．处理部分对该三相信号进行相应的处理，即可得到转子位置．转子磁场旋转一周，理想的三相感应电压信号曲线如图3所示．

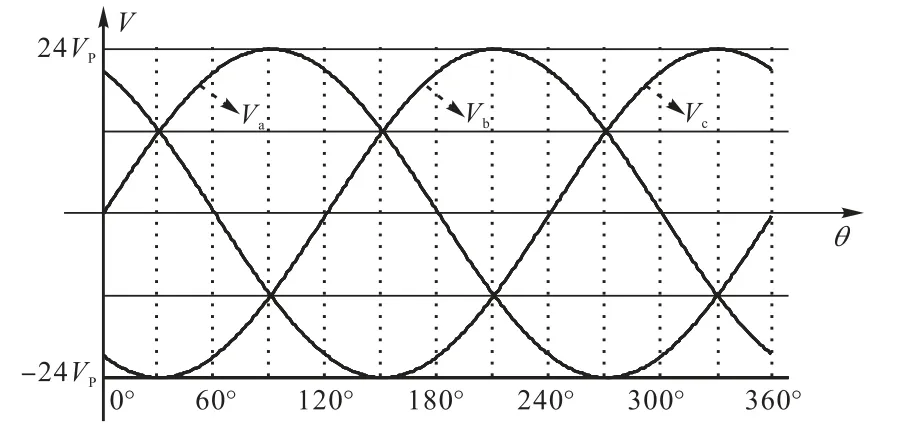
图3 一周期内三相磁敏元件输出信号Fig.3 Output signal of three-phase magnetic sensitive organs in one cycle

为获得更快的处理速度和精度，本文编码器采用基于查表方式的信号处理算法．首先通过编码器校准系统，将编码器转子(磁场)机械角度(0°～360°)，与定子(磁敏元件输出的)三相电压信号之间的对应的关系制成数据表并存储起来．编码器工作时，只需要接收三相电压信号，就能在数据表中找到其对应的绝对角度．

相对于其他单极式磁电编码器常用的反正切数据处理方法[7]，查表法极大地简化了运算，很大程度上提高了信号处理速度．实际应用中，先将磁钢环(转子)和3对磁敏元件(定子)安装在电机上，再用校准系统校准，在每台电机和其编码器之间建立一对一的数据表，这样可有效避免机械加工和装配精度对编码器精度的影响．

本试验系统中 AD采样分辨率为 4 096，差分后的分辨率为8 192，对应的数据表长度约为24 576，角度值为 16位数，需要约 25×103字节(16位)的存储空间．

笔者提出的磁电编码器，对机械精度、磁场和模拟信号的线性度要求都不高，通过改善信号质量和改进校准系统来提高编码器精度的潜力巨大．

1.4 工作时序和滞后时间

从工作原理可知，提出的编码器不像一般光电编码器那样实时上报角度，而采用被动的定时同步串口通信的形式上报角度．通信方式如图 4所示，编码器与伺服控制系统通过同步串行接口以全双工通信模式来实现角度上报．

图4 同步串行通信Fig.4 Synchronous serial communication

图 4中主通信端(Master)代表控制系统，其通信所得到的反馈角度，是从通信端(Slave)一段时间之前的采样处理结果．在高转速下，这段时间产生的转子位置信号滞后尤为明显，直接把此反馈角度作为当前转子角度进行矢量控制，会使电流矢量偏离正确方向，严重时会造成控制失效，必须准确补偿滞后量．要想计算滞后量，首先要通过分析编码器工作时序得到滞后时间．

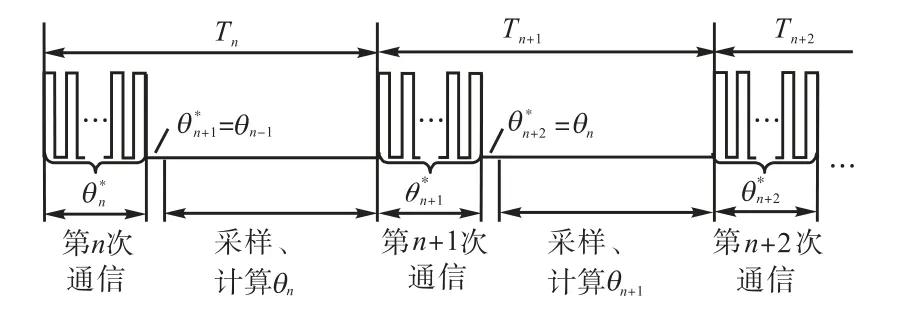
图5 编码器工作时序Fig.5 Working sequence of encoder

图 5中一个周期即伺服控制系统的采样和控制周期为 Ts，通信时间设为 tc，通信结束后赋值和进入采样计算中断的时间是te，即每个周期tc+te时间后进行采样．则角度滞后时间是 2Ts-(tc+te)，用控制周期的倍数表示为 κTs，即

2 高速电机矢量控制

2.1 永磁同步电机模型

在转子 d-q坐标内，将定子电流矢量i分解成励磁电流分量 id和转矩电流分量 iq，两分量正交，彼此独立，可分别调节．如图6所示．

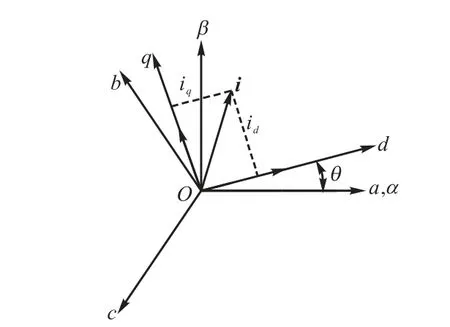
图6 空间矢量坐标变换Fig.6 Space vector coordinate transformation

对永磁同步电机做如下假设：

(1)电机三相绕组完全对称，电机无齿槽效应，电机气隙磁势在空间中正弦分布；

(2)铁芯涡流、饱和及磁滞损耗忽略不计；

(3)忽略漏磁通的影响，忽略磁阻转矩的影响；

(4)转子为永磁体，其磁链幅值大小恒定为fΨ，在气隙中呈正弦分布．

由于工作在低饱和区，高速永磁同步电机的交、直轴电感接近，所以高速永磁同步电机的数学模型可以采用线性模型

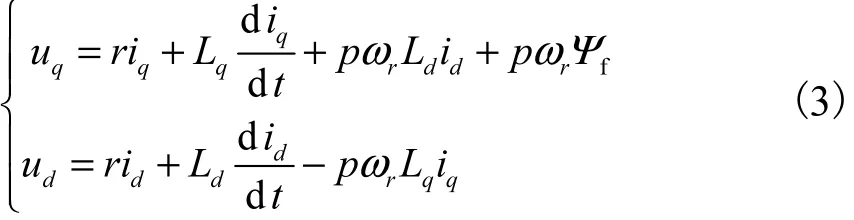
式中：uq、ud为变换后的电机交、直轴电压；iq、id为电机交、直轴电流；p为电机极对数；fΨ为永磁体产生的磁链．

电机的转矩方程式为

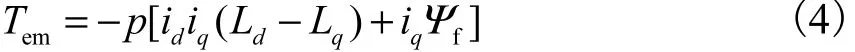
如果控制di等于 0，则转矩emT 只与转矩电流 iq有关，即

采用这种对磁场电流和转矩电流进行解耦控制的矢量控制方式，可以使永磁同步电机具有和传统直流电机相同的运行性能[8-9]．

2.2 控制过程分析

控制过程如图7所示．三相电流反馈经过Clarke变换和Park变换后，得到反馈值id和iq，这2个值与电流指令进行差分后经过控制器可得到 d-q轴电压ud、uq，d-q轴电压再经过 Park变换和 Clarke变换的逆变换可得到给电机的三相电压指令 ua、ub、uc，经脉宽调制(PWM)得到三相桥式电路驱动信号，驱动功率开关管向电机供电，产生转矩驱动电机旋转．

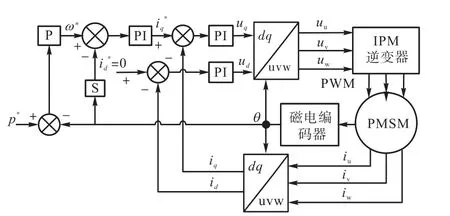
图7 矢量控制过程Fig.7 Vector control process

将定子电压在定子静止坐标系和转子坐标系下用空间矢量的形式表示为

将 Vdq乘以旋转矢量算子ejθe，实现定子电压由转子旋转坐标系到静止坐标系的变换，即 Park逆变换，即

图8为电流采样和计算、PWM输出的时序图．

反馈电流的采样频率与控制频率同步，在每个控制周期开始时进行．由于采用了离散控制算法，PWM输出滞后了一个采样周期，PWM 输出在 t+Ts到t+2Ts时间内有效．在静止坐标系下，在 t+Ts到 t+2Ts时间内定子电压矢量应为

图8 电流采样和PWM输出时序Fig.8 Current sampling and PWM output sequence

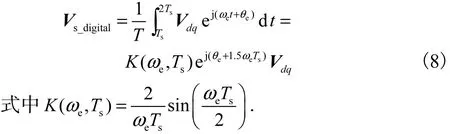
由式(7)与式(8)可以看出，实际的电压输出与理想的电压输出存在一定比例误差．此比例误差可表示为

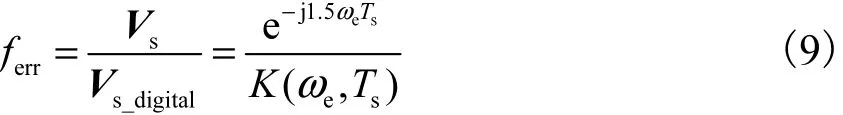
由式(9)可以看出，电压矢量的幅值衰减，相位滞后 1.5个采样周期．PWM 频率一定，电机转速较高时，PWM 频率与输出电压的基波频率的比值较小，相位滞后较大，如果不对滞后进行补偿，控制滞后会使得电流调节器的动态响应变坏，严重时会造成系统不稳定．

在相位滞后不是非常大的情况下，幅值衰减很小，为补偿控制滞后带来的影响，可以采用相位超前方式进行补偿，即在实现定子电压由转子坐标系到两相静止坐标系的变换时乘以旋转矢量算子，补偿后的定子电压矢量为

2.3 角度滞后误差补偿

高速电机矢量控制过程中，转子位置精度直接决定了电流矢量的控制精度．

电流反馈采样在控制周期开始时刻进行，而通过分析编码器工作时序(见第 1.4节)可知，此时，控制系统得到的角度反馈滞后时间为 κTs．假设电机匀速运行，转速为ω，则角度补偿量(滞后量)为

2.4 补偿误差分析

电机匀速运行时，按式(11)计算补偿量不产生理论误差．但在电机加减速运行时，按此式计算出的补偿量存在一定的理论误差，对此误差进行分析．

角度滞后时间很短，不考虑此时间内的加速度变化．设电机的角加速度为α，则上述补偿公式中，转子转速ω为未补偿前角度采样之前一周期内的平均速度．则编码器采样时的瞬时转速应为s(/2)Tωα+，对应滞后时间κTs后，角度补偿量应为

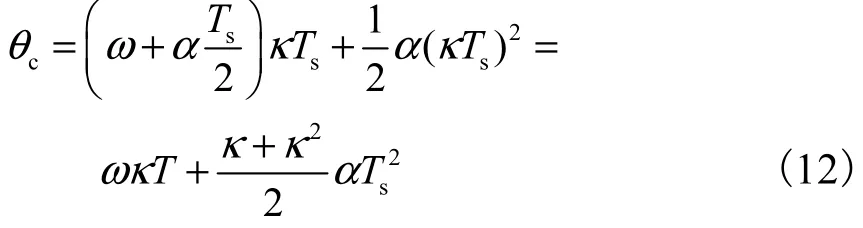
比较式(11)和式(12)，式(11)的补偿误差为

在实验系统中，采样控制周期 Ts=50，μs，通信时间 tc=8，μs，通信结束到进入采样计算中断的时间te=2，μs，代入式(2)，得 κ=1.8，则

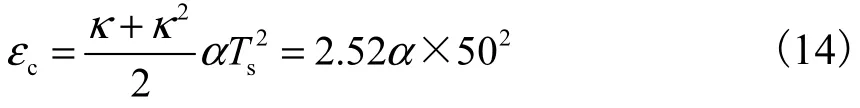
设极限加速情况为电机用0.1 s从静止到加速到100，000，r/min，即角加速度α=0.000，006 °/μs2．若按式(11)补偿，则由此加速度产生的补偿后的位置误差为cε=0.037 8°．这个角度偏差对控制计算的影响甚微，可以忽略，即完全可以按式(11)补偿滞后量，不需考虑加速度带来的影响．

3 实验验证

设计的单极式磁电编码器所用霍尔传感器带宽为 200，kHz，考虑到响应相位滞后的影响，对频率10，kHz以内的模拟信号响应可视为不失真，即正常工作转速可达到 600，000，r/min．编码器实物如图 9所示．

图9 单极式磁电编码器及安装位置Fig.9 Single-pole magnetic encoder and its installation position

此编码器输出16位绝对值角度，精度能达到12位(约5.27′)以上，满足高速电机对编码器的精度要求．

高速电机的设计较困难，为了验证本文所提控制方法的有效性，设计了一台 4对极、额定转速为20，000，r/min、额定功率为 600，W 的电机．实验平台包括已安装了单极式磁电编码器的高速永磁同步电机、控制系统、示波器和电子测速仪，如图10所示．

图10 系统实验平台Fig.10 Test bench

空载下，速度指令从零加到 15,000,r/min，做匀速控制，电子测速仪显示的速度为 15,007,r/min；速度指令加到 20,000,r/min，做匀速控制，电子测速仪上显示的速度为20,010,r/min．单片机内部定时器误差、外部晶振误差、控制误差和测量误差等都是造成该误差的可能因素．

转速设定分别为15,000,r/min和20,000,r/min时的电机单相电流波形分别如图 11(a)和(b)所示．由图11可以看到，电流变化频率为速度的4倍，幅值比较均匀，达到了预期的控制要求．

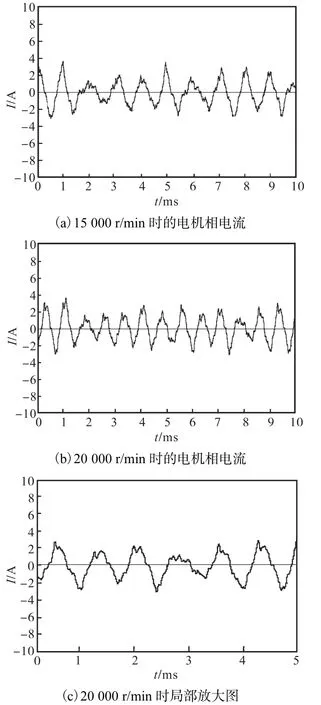
图11 单相电流曲线Fig.11 Curves of single phase current

4 结 语

本文提出了一种利用单极磁电编码器实现高速电机矢量控制的方法．该编码器以通信触发采样方式工作，同步串行通信方式上报角度，精度满足矢量控制需要．控制系统通过在高速运行中定时通信获得转子绝对位置，并对信号滞后产生的位置反馈误差进行补偿，得到准确的位置信号，从而可对高速永磁同步电机实现矢量控制．实验在转速为 20,000,r/min的条件下验证了该编码器和控制方法的有效性．结果表明，这种方法有效地利用位置传感器实现了高速电机矢量控制．

［1］Bianchi N，Bolognani S，Luise F. Potentials and limits of high speed PM motors [J].IEEE Trans on Industry Applications，2004，40(6)：1570-1578.

［2］Kim H，Harke M C，Lorenz R D. Sensorless control of interior permanent-magnet machine drives with zero phase lag position estimation [J].IEEE Trans on Industry Applications，2003，39(6)：1726-1733.

［3］Shinnaka S. New sensorless vector control using minimum-order flux state observer in a stationary reference frame for permanent-magnet synchronous motors [J].IEEE Trans on Ind Electronics，2006，53(2)：388-398.

［4］Moussa M F，Gaber Y，El Attar M. Vector control drive of permanent magnet motor without a shaft encoder[C]//Power System Conference．Aswan，Egypt，2008：249-254.

［5］Shinnaka S. New mirror-phase vector control for sensorless drive of permanent-magnet synchronous motor with pole saliency [J].IEEE Trans on Industry Applications，2004，40(2)：599-606.

［6］Carr J，Desmulliez M，Weston N，et al. Optical encoder readhead chip[C]//Electronics System-Integration Technology Conference．Greenwich，UK，2008：797-802.

［7］Hagiwara N，Murase H. A method of improving the resolution and accuracy of rotary encoders using a code compensation technique[J].IEEE Trans on Instrumentation and Measurement，1992，41(1)：98-101.

［8］Bae Bon Ho， Sul Seung Ki， Kwon Jeong Hyeck， et al.Implementation of sensorless vector control for super high speed PMSM of turbo-compressor [J].IEEE Trans on Industry Applications，2003，39(3)：811-818.

［9］Konghirun M， Xu L. A dq-axis current control technique for fast transient response in vector controlled drive of permanent magnet synchronous motor[C]//Power Electronics and Motion Control Conference．Xi’an，China，2004，3：1316-1320.

［10］Kim Y S，Choi Y K， Lee J H. Speed-sensorless vector control for permanent-magnet synchronous motors based on instantaneous reactive power in the wide-speed region[J].IEE Proc-Electr Power Appl，2005，152(5)：1343-1349.

［11］Mohamed Y A-R I. Adaptive self-tuning speed control for permanent magnet synchronous motor drive with dead time[J].IEEE Transactions on Energy Conversion，2006，21(4)：855-862.