基于弹性尺度的有向生长法的弥散型区域分割
2010-05-10侯谨毅解以扬
王 萍,张 艳,侯谨毅,解以扬
(1. 天津大学电气与自动化工程学院天津市过程检测与控制重点实验室,天津 300072;
2. 天津市气象局,天津 300074)
弥散型区域的图像特点是区域内不具连通性,在其内部,取值一致的像素点或子区域若近若离,形成对依据一致性原则进行对象分割的困难.
就相距较远的多个弥散型区域而言,数学形态学的膨胀法可以做为弥散区域连通化的有效方法[1],即经数次膨胀使区域连通后,再使用相同的结构元素进行相同次数的腐蚀,便可形成弥散型区域对象的分割模板.然而,当多个弥散型区域相距较近甚至局部相连时,膨胀的结果往往在区内连通化的同时造成区间的相互粘连,无法形成正确的分割.
就台风云系而言,其降水强度及降水范围与螺旋云带紧密相关[2],同时,定位台风中心所需的重要信息也蕴含于螺旋云带中[3].由多普勒雷达探测到的台风云系图像,经初分割处理后,形成的就是多个相距较近的弥散型区域,笔者就此提出一种具有弹性尺度的有向生长方法,以解决台风云系中螺旋云带的自适应分割.
1 弥散型台风螺旋云带区的形成
云团主要由具有一定密度的云雨粒子群构成,当多普勒雷达波对其进行探测时,遇到云雨粒子则形成反射波,反射波的反射率强度与粒子的大小及密度密切相关.图 1分别给出了“桑美”和“百合”在发展过程中的多普勒雷达反射率的 15级灰度图像(背景色除外),图中,灰度级越高,反射率值越大[4].表 1给出了它们各自的灰度级所拥有的像素点数和灰度级自高到底的累计份额.由表1可以看出:
(1) 位于螺旋云带的反射率R普遍较强(图1(a):R* ≥ 5 0 dBz ,图1(b):R * * ≥ 4 5dBz);
(2) 不同的台风云系,其螺旋云带主体的反射率强度范围不尽相同(R* ≠ R**);
(3) 螺旋云带主体的灰度等级与灰度累计值发生第1次10%以上的跃变相对应;
(4) 看上去,螺旋云带像是被镶嵌在其他多种灰度表征的整体云系的背景中.
基于此,估计自适应初分割阈值α的方法如下:
在台风云系的反射率图中,设各灰度级的总像素点数为N,反射率值等于 Ri的像素点数为 Ni,则反射率强度 Ri所占份额为

自高到低计算反射率强度的累计份额为

使用以上方法对图像进行初分割,结果如图2所示,借助图2不难做出如下归纳:

图1 台风云系的雷达反射率图像Fig.1 Radar reflectivity maps of typhoon cloud systems
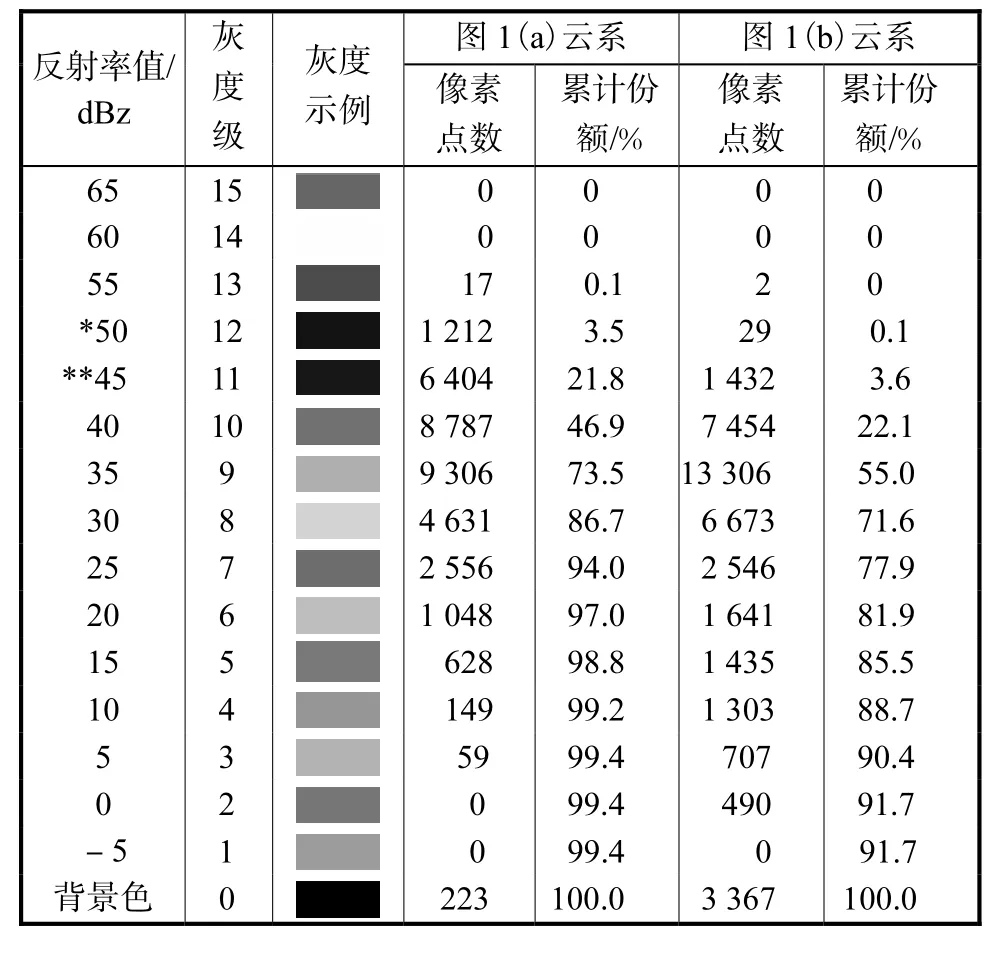
表1 图像中各灰度级像素数目统计表Tab.1 Statistical table of pixel numbers in each grayscale
(1) 宏观上,弥散型的点或子区域勾勒出了台风云系的螺旋性走向;
(2) 细节上,各点的分布是随机的,它们或抱团形成局部的连通子域或分离形成内部的孤立点;
(3) 整体上,呈现若近若离的非联通态势.
云团内云雨粒子尺度及密度的非均匀性是造成以反射率强度为阈值的初分割区呈弥散型的内因.从图像分析和识别的角度看,这种连通性很差的弥散型区域不利于后续的基于螺旋云带的中心定位和雨量估计.

图2 自适应初分割的二值图Fig.2 Binary images of adaptive primary segmentation
2 连通化处理方法研究
2.1 弹性尺度下的有向膨胀
一般,通过数学形态学的“膨胀”处理,可以增强弥散型区域内部的连通性.图3是采用3×3的结构元素对图2连续做2次膨胀的实验结果.

图3 对弥散型螺旋云带区进行膨胀处理的效果Fig.3 Dilated images of diffused spiral cloud bands
经多次实验可以发现,当使用经典膨胀算法对弥散型区域进行膨胀时,不论结构元素的类型、尺度以及膨胀次数如何,均会出现示例中的如下问题:
(1) 膨胀运算使弥散型区域内连通化的同时引发了区间的粘连;
(2) 非螺旋云带的噪声被扩大了.
问题(1)淡化了有用的螺旋云带信息,问题(2)强化了无用的噪声.究其原因,是因经典的膨胀算法无方向性、无选择性所致.
设图4为台风云系螺旋云带模板,点划线为螺旋带状区的中心线,虚线勾勒出带状区的范围,小实心块为经自适应初分割后的云区,阴影区是膨胀后的生长区.其中,图 4(a)是采用经典膨胀法处理后的局部示意,显然,在子块1与子块2连通的同时,块1与块4被错误地粘连;图4(b)和(c)是选择性膨胀的结果,即块1仅向区内膨胀.图4(b)与(c)的区别是后者在一次膨胀中,结构元素的尺度是弹性的,即设结构元素为圆形,其半径r取决于子块i的待膨胀点k与径向相邻块j的距离kd,特别取

式中β为圆形结构元素尺度的上限值.
为达到图4(c)的效果,需要解决2个问题.
(1) 相邻块的确定;
(2) 距离的计算与膨胀元素尺度的调整.
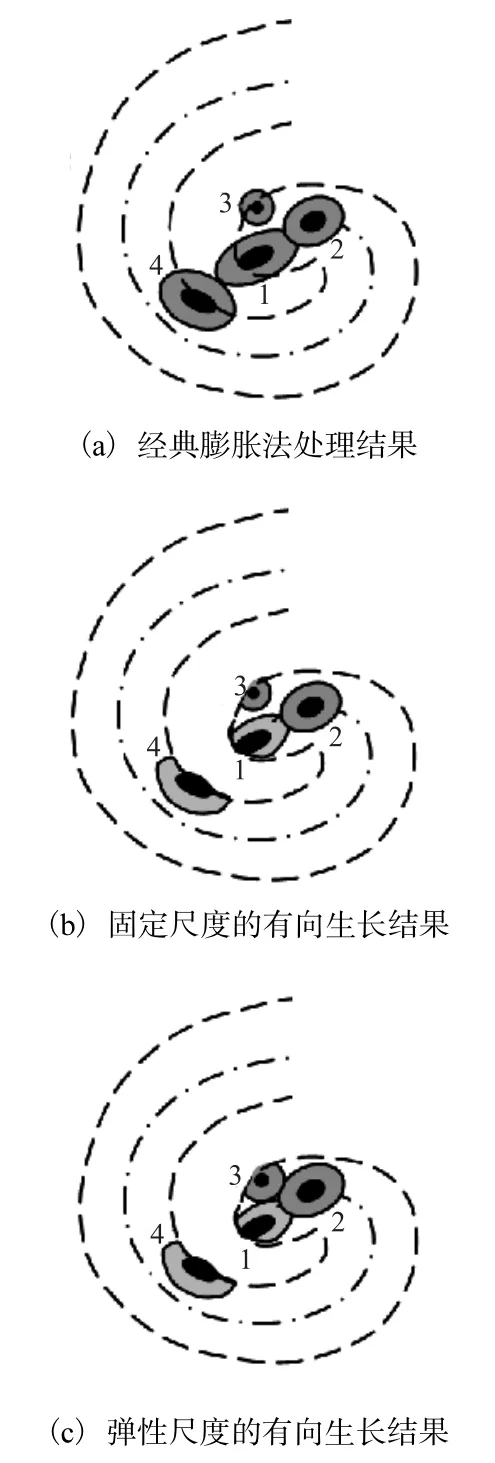
图4 全向生长与有向生长Fig.4 Omnidirectional growth and directed growth
2.2 相邻块的确定
将螺旋云带模板视为处处连通的,则位于图4中的块1与块4的测地距离要远远大于欧氏距离,而块1与块 2、块 3的测地距离与欧氏距离近乎相等,那么,前者则定义为非相邻块,后者则定义为相邻块.从统计角度看,弥散型区内的块间欧氏距离小于弥散型区间的块间欧氏距离.

根据先验知识和实验分析可知,弥散型螺旋云带区内的绝对距离短且集中、区间距离大且分散,形成图5直方图中左侧的高峰和高峰跌落后的平稳变化,设取值0到v的绝对距离数通过直方图面积得到
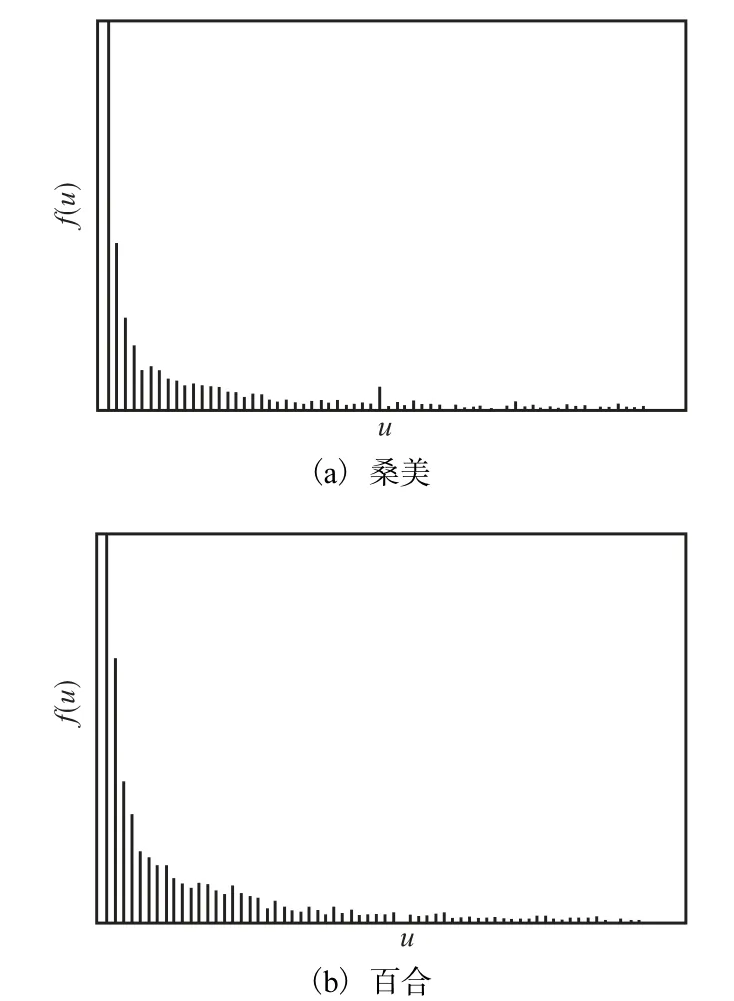
图5 相离邻点间水平、垂直向绝对距离分布Fig.5 Distribution maps of absolute distance between adjacent points in horizontal direction and,vertical direction
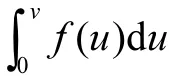
则根据直方图面积的变化率
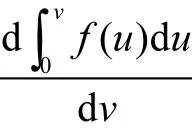
将所有绝对距离聚成“短绝对距离”类和“长绝对距离”类,再根据“短绝对距离”类的均值1μ、标准差1σ和“长绝对距离”类的均值2μ构建块间是否相邻的判据如下.
判据设块 I边界上存在一点i,从该点沿水平向或垂直向搜索到块J边界上的一点j,若
则块J与块I相邻,其中

2.3 生长策略与生长尺度的确定
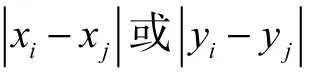
由于在相邻的块I与块J上,一定存在局部的相邻边界,而相邻边界上各相邻点的水平或垂直距离均小于r,一旦将这一距离确定为生长尺度,则生长尺度将视实际的距离值而定,因此是弹性的、多尺度的.
3 多尺度有向生长算法
多尺度有向生长算法步骤如下:
步骤 1对经自适应初分割后形成的弥散型螺旋云带区域(MN×),计算相离邻点间水平、垂直向绝对距离,聚类[8-10]后,经统计计算得到相邻判据所需阈值r.

以上算法的有向性和多尺度性体现在步骤 2和步骤 3的(3)中.算法的运行次数则取决于r值的大小.一般,为避免有向生长过程的区间粘连,应将r取得小一些,例如取

这时应适当增加运行次数.
将以上算法运用于自适应初分割后的弥散型螺旋云带,再配以补空洞,去杂点,边界修整等后续处理,均得到比较好的台风云系中的螺旋云带图像,图6给出了其中的2个示例.

图6 多尺度有向生长效果Fig.6 Images of multi-scale directed growth
4 结 语
如果将弥散区视为对象整体的话,区内相离的块是相邻的,区间的块是不相邻的.则基于相离块邻点间的横、纵向绝对距离的聚类分析能够自适应地完成相离块(点)的相邻和非相邻的标定.特别注意到 2类对象反映在绝对距离直方图面积变化率上的显著性差异,并借此实现聚类,然后利用类的分布参数构建用于类标定的阈值,方法简单有效、具有自适应性.
为将弥散区内的子块间连通,同时又不向区外扩展,需要将区内子块进行定向膨胀(生长)、区边子块进行有向膨胀(生长),构建了基于点的相邻判据,沿块边界点逐点判断并确定是否向外生长,以及生长的尺度,解决了弥散区域连通化处理后的自适应分割问题.
[1]戴青云,余英林. 数学形态学在图像处理中的应用进展[J]. 控制理论与应用,2001,18(4):479-482.
Dai Qingyun,Yu Yinglin. The advances of mathematical morphology in image processing[J].Control Theory and Application,2001,18(4):479-482(in Chinese).
[2]愈小鼎. 多普勒天气雷达原理与业务应用[M]. 北京:气象出版社,2006:102-183.
Yu Xiaoding.The Principle and Application of DopplerWeather Radar[M]. Beijing:Meteorology Press,2006:102-183(in Chinese).
[3]韩 瑛. 台风螺旋结构的分析[J]. 南京大学学报,2007,43(6):572-581.
Han Ying. On the spiral structure of typhoon[J].Journal of Nanjing University,2007,43(6):572-581(in Chinese).
[4]Wang Ping. Local spiral curves matching based on Hough transformation and center auto-locating of developing typhoon[J].Transactions of Tianjin University,2006,12(2):142-146.
[5]李海芳,王 莉. 基于空间直方图的免疫图像聚类算法研究[J]. 计算机工程与设计,2008,29(11):2932-2935.
Li Haifang,Wang Li. Research of immune image clustering algorithm based on space histogram[J].Computer Engineering and Design,2008,29(11):2932-2935(in Chinese).
[6]王燕妮,樊养余,毛 力. 基于感兴趣区域轮廓的图像分割方法[J]. 现代电子技术,2008,279(16):133-135.
Wang Yanni,Fan Yangyu,Mao Li. Image segmentation method based on silhouettes of interested region[J].Modern Electronics Technique,2008,279(16):133-135(in Chinese).
[7]陈方昕. 基于区域生长法的图像分割技术[J]. 科技信息,2008(15):58-59.
Chen Fangxin. Image segmentation technology based on region growing method [J].Science and Technology Information,2008(15):58-59(in Chinese).
[8]翁秀梅,肖志涛,杨洪薇. 基于边缘检测和区域生长的自然色图像分割[J]. 天津工业大学学报,2008,27(1):50-52.
Weng Xiumei,Xiao Zhitao,Yang Hongwei. Natural color image segmentation based on edge detection and region growing[J].Journal of Tianjin Polytechnic University,2008, 27(1):50-52(in Chinese).
[9]Fan Jianping,Yau D K Y. Automatic image segmentation by integrating color-edge extraction and seeded region growing[J].IEEE Transactions on Image Processing,2001,10(10):1454- 466.
[10]Li W,Huang H,Zhang D. A color image segmentation method based on automatic seeded region growing[C]//Proceedings of the IEEE International Conference on Automation and Logistics.Jinan,China,2007:1925-1929.
