三维电磁场有限元数据到有限差格式的转换算法

龚海军，徐达鸣，傅恒志

(哈尔滨工业大学材料科学与工程学院，哈尔滨150001，331ghj@163.com)

电磁约束凝固成形和电磁连铸等电磁材料加工及其数值模拟技术是目前研究较为活跃的领域［1－3］.电磁场作用下的合金凝固是一个多场作用下的热量、质量及流体动量强耦合传输过程［4］，如冷坩埚电磁定向凝固过程中，高温金属熔体与冷坩埚壁之间存在剧烈的传热，同时电磁场对冷坩埚中的金属熔体有高密度的加热、搅拌及约束作用［5－8］.对这些发生在四维时空中的复杂多物理场耦合问题，通常需要采用有限元(FEM)、有限差(FDM)或有限体积(FVM)法等进行数值解析.许多多物理场相互作用下的复杂场量耦合计算常联合使用FEM和FDM/FVM来进行，并已成为一种趋势［9－12］.由于FEM和FDM/ FVM剖分网格空间结构差异较大，高效率的多场FEM/FDM耦合计算须有效解决两种数据格式的匹配，特别是三维FEM→FDM的数据格式转换问题.

为有效地将高效率凝固耦合传输统一模型［13－15］应用于电磁凝固传输计算中，需采用FEM与FVM相结合的耦合计算方法，即应用通用有限元软件ANSYS进行电磁场量的计算，采用基于有限差法的凝固传输统一数学模型计算电磁凝固耦合传输过程.为此，本文提出一种将电磁场FEM计算结果转换成凝固传输耦合计算所需的FDM/FVM数据格式的有效方法.

1 三维电磁场计算模型

为检验本文数据转换方法和程序的普适性，首先对冷坩埚电磁定向凝固系统、电磁连铸系统、电磁熔炼和搅拌系统中的电磁场进行计算，然后将有限元格式的数据转换为限差格式并显示.其中，冷坩埚电磁定向凝固系统造型和剖分如图1所示，模型比例为1∶1.本文计算模型采用ANSYS基于节点的方法，谐波模型除远场空气采用INFIN111单元外，其余均采用SOLID97单元，空气单元定义磁矢位自由度，导体单元定义磁矢位和电压自由度.

图1 冷坩埚电磁定向凝固计算模型结构及FEM网格剖分

2 三维有限元计算结果的有限差转换

2.1 ANSYS有限元计算结果的存储形式

ANSYS节点法求解电磁场得到的是节点解，对于静磁场计算结果的插值转换，需要输出结点坐标信息(*c.lis)、单元 －材质 －节点信息(*mn.lis)、节点形式的磁感应强度结果(*b.lis)、有单元信息的磁感应强度结果(*e.lis)4个文件;对谐波和行波磁场，则还需另外输出焦耳热(*j.lis)和电流密度(*d.lis)两个结果文件.实际电磁计算中由于模型形状复杂，无法全部用六面体单元剖分网格，在某些区域会以退化的单元形式出现.通常情况下，8节点空间等参数单元合并其中1个或几个节点，便可以退化为4～7节点的单元.在ANSYS模型中，六面体形单元只以楔形、金字塔形和四面体形3种退化单元形状来协调网格划分，如图2所示，不会出现7节点六面体单元(即图2(a)中六面体合并任意相邻两点).故一般情况下，电磁场的计算值存储于4种不同形状和不同有效节点数目的单元或单元节点上.

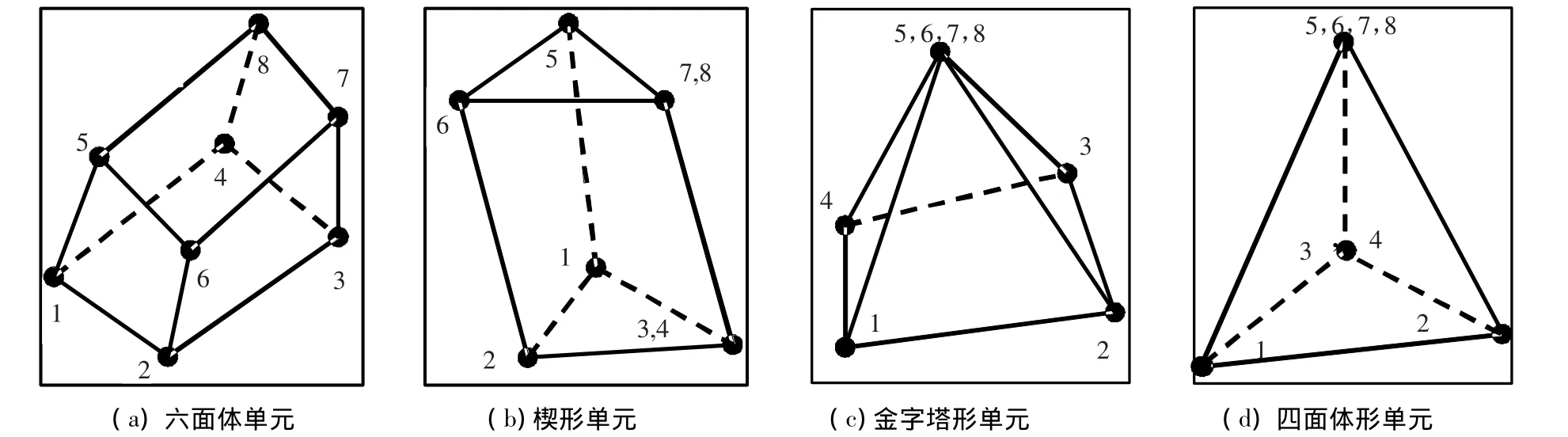
图2 ANSYS三维电磁场有限元计算所用的4种单元形状

2.2 有限元计算结果的有限差转换

为将3D－EM的FEM计算结果应用于电磁凝固耦合传输计算，需将FEM数据向FDM形式转换.对于如图2(a)所示的三维一次8节点六面体单元，设:A为其内部任意一点，8个节点按右手定则顺序依次对其编号为i，j，k，l，m，n，p，q.根据有限元线性插值理论，电磁场量节点值在单元内沿3个坐标轴(x，y，z)方向上将呈线性变化，x方向分量u=u(x，y，z)可写成

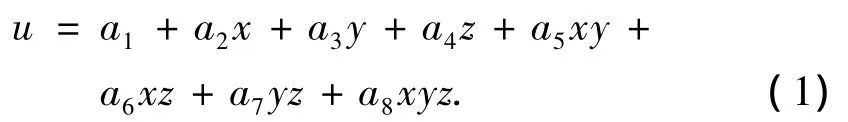
式中:a1，a2，…，a8分别为待定系数.六面体单元内任意一点A在x方向上的电磁场分量u可写成

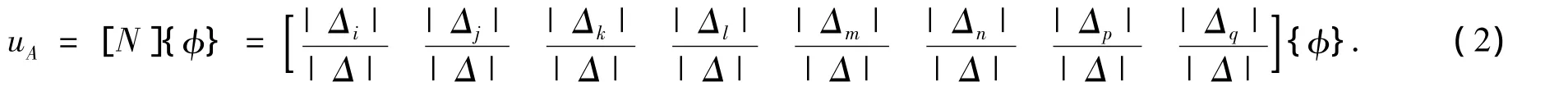
其中:

式中:［N］为形函数，是坐标x，y，z的函数，{φ}为六面体单元8个节点在x方向的电磁场分量构成的列向量，由 ANSYS计算并导出.|Δi|，…，|Δq|分别为将|Δ|内的坐标值xi，yi，zi，…，xq，yq，zq替换为xA，yA，zA.同理，y，z方向的电磁场分量v，w的插值计算可类似地写出.

对于在如图3(c)所示的四面体一次单元，同样设A为四面体内部任意一点，4个节点按右手定则顺序依次对其编号为i，j，k，l.则A点处某一电磁场量值为

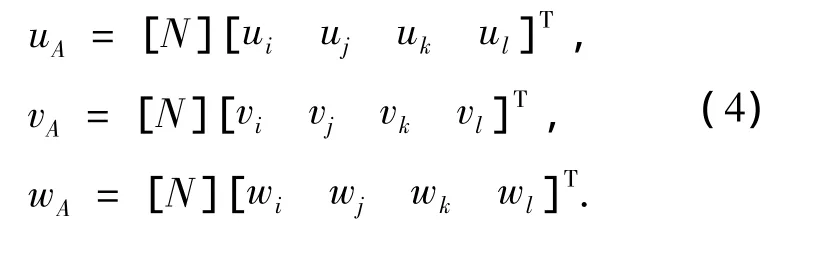
其中:

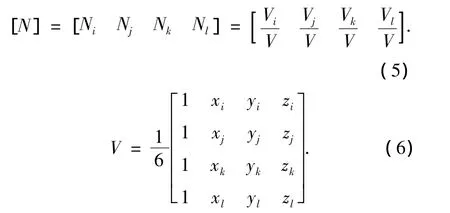
式中:V为由i，j，k，l 4点构成的四面体体积，Vi，Vj，Vk，Vl分别为四面体内的A点取代i，j，k，l构成的四面体体积.

其它两种形状单元的形函数可类似导出.显而易见，采用四面体及其形函数进行线性插值计算相对其它单元形状要简单和方便，故本文将六面体形、楔形和金字塔形等非四面体单元都分解为便于插值计算的四面体单元来处理.

根据空间几何关系，任意六面体形单元可划分为5个或6个四面体，且分别有两种划分方式，以A5、B5和A6、B6表示，如图3(a)、图3(b)所示.A5型划分为6 873，6 581，6 831，6 321，8 314，B5型划分为7 652，8 754，2 574，7 324，1 245;A6型划分7 652，2 573，5 321，8 753，8 513，1 483，B6型划分7 652，8 752，5 218，7 832，1 238，1 348.为减少计算工作量，本文将六面体单元划分为5个四面体，楔形和金字塔形也做类似的分解处理，所有分解出的四面体子单元及其节点将携带原母单元及其节点上的所有信息.

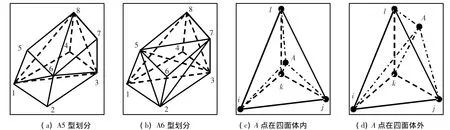
图3 六面体FEM单元分解为四面的两种方式及FDM中心点与分解的四面体FEM的对应关系

确定了非四面体单元分解次序，便可通过体积判断来对FDM中心点与FEM单元进行查找和对应.具体方法是:如果FDM中心点A落入某非四面体FEM单元分解出的一个小四面体内(图3(c))，则A点与此小四面体4个顶点组成的4个新小四面体的体积和与原小四面体体积将相等(＜ε，ε为一误差限)，那么便认为该FDM中心点落入此四面体FEM单元中，随后以其对应的四面体的4个节点来线性插值;如果FDM中心点A落入小四面体外(图3(d))，那么根据四面体体积式(6)，在顶点次序为非右手定则顺序的情况下，A点与此小四面体4个顶点组成的4个新小四面体的体积和将为负值或一小于原小四面体体积的值.ANSYS网格原本为四面体形的单元无需再分解，可直接进行体积判断来与FDM单元查找对应，确认对应关系后便可对场量进行插值计算.根据线性插值理论，上述插值计算方法对FDM中心点落在FEM单元表面、边界或单元节点上的情况同样适用.

需指出的是，ANSYS计算的焦耳热和电流密度结果是按单元输出的，不能按上述方式直接插值计算，此时FDM中心点与FEM单元对应获取焦耳热和电流密度有两种方案:1)当某FDM中心代表点落入某单元时，就以该单元的焦耳热和电流密度值作为FDM中心点的相应值，其缺点是当多个FDM中心代表点落入同一个FEM单元时取值都相同，不能很好显示焦耳热和电流密度值沿空间位置连续变化的趋势，且在靠近表面处焦耳热和电流密度值的插值结果将偏低;2)将FEM单元的焦耳热和电流密度值向单元的节点进行“节点化”处理.即对于所有节点，先统计同一节点属于多少相邻单元共用，然后将此节点上的焦耳热和电流密度值取共用该节点的单元焦耳热和电流密度值的算术平均，最后再按上述处理磁感应强度的方法来查找对应和插值计算.即本文选用第2套方案，这样处理的结果，也不可避免地会导致紧邻样件表面处焦耳热和电流密度值的插值结果偏低，但可以通过在场量梯度较大区域加细网格，保证足够的精度.

基于上述有限元的线性插值原理和所提出的实施方案，本文采用Fortran95语言编写了三维FEM→FDM数据转换程序，具体流程如图4所示.

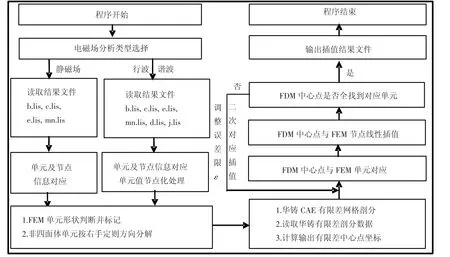
图4 FEM→FDM数据转换计算程序流程

对于一些几何形状复杂的模型，经过一次完整循环，有时会出现某些有限差中心点找不到与之对应有限元单元的情况，也就是说没有得到插值结果，这时就需适当调整误差限ε，进行二次查找对应和插值，一般经过二次查寻都能找到对应单元;几何形状规则的模型，不会或很少出现需要二次查寻和对应的情况.通常情况下，为了提高耦合计算精度和适应模型中变尺寸区域，FDM网格比有限元单元小而多，FEM/FDM转换计算的单元对应过程中可能有多个FDM中心点落入同一FEM单元，如按六面体和五面体形函数进行插值计算，则这些落入同一FEM单元的多个FDM中心点的插值结果相近，这样便不能很好反映出因坐标变化而带来的场量变化;如将非四面体FEM单元分解，当 FDM中心点落入某一非四面体FEM单元分解出的小四面体后，以此中心点所在的小四面体节点值进行插值计算，而当下一个FDM中心点再次落入同一非四面体FEM单元时，则以其所对应单元的另一分解出的小四面体节点值进行插值计算.也就是说，不同时以非四面体单元的所有节点来插值，这样便增加了插值结果对坐标的敏感性，这是分解非四面体单元进行插值计算的另一优点.本文计算和转换工作在1台CPU主频为3.0 GHz、内存为3.0 GB的PC上运行，各计算模型数据及转换计算用时对比如表1所示.

表1 各计算模型FEM→FDM数据转换计算结果对比

3 三维矢量场后处理显示对比

目前有许多商用软件自备后处理模块，可显示3D标量和矢量场，但是这些软件的显示模块通常不通用.在凝固传输过程的研究中，尤其是对于涉及凝固的流动过程，纯液相区中的流速与固液两相区中的速度相比一般要大1～2个数量级以上，而这两个区域的流动行为对于凝固缺陷如宏观偏析等的定量预测极其重要，需要区分纯液相区和固液两相区采用双速度标尺才能同时有效显示整个凝固铸锭/铸件中的流场分布.为此，本文通过Visual Fortran 6.6A的QuickWin应用程序平台，用Fortran 95语言自行编写了集FEM/FDM数据转换计算和铸件凝固传输数值模拟数据3D图形显示功能于一体的后处理程序.

图5为冷坩埚电磁定向凝固系统内TiAl合金锭的各电磁场量对比，其中，图5(a)、图5(c)、图5(e)是ANSYS计算显示的结果，图5(b)、图5(d)、图5(f)是本文程序将ANSYS计算结果转为有限差后的显示结果.由图5(a)可见，磁感应强度在线圈所缠绕的中部区域最强，矢量方向沿合金铸锭向下，图5(b)是数据换后的等轴测显示结果，可见，转换后磁感应强度的大小和方向与转换前是一致的.图5(c)、图5(e)所示分别为ANSYS计算输出的上下锭中焦耳热和电流密度分布，相应的转换结果如图5(d)、图5(f)所示，可见转换后的电磁场量分布与转换前吻合.

图5 上、下钛合金铸锭中电磁场的ANSYS模拟结果与本文FEM→FDM数据转换后结果的对比

本文编写的后处理程序可根据实际需要，选择等轴测或斜二测显示二维和三维场量图像，如果必要，3个坐标轴方向还可以任意互换，使图像在屏幕上以不同视角显现.图6(b)即为连铸熔池内静磁场的斜二测分层显示，其分布规律和数值大小与转换前(图6(a))一致，且水嘴出口处的液流和磁场值都显示正常.图6(c)、图6(d)所示为某一碳化硅坩埚内铝合金熔体的磁感应强度［16］转换前后对比，结果表明:对于双变曲率的曲面结构，本文提出与开发的FEM→FDM转换算法和计算、显示程序同样适用.

4 结论

1)将六面体有限元剖分单元及其退化单元统一地分解为简单四面体单元，然后进行FEM→FDM三维空间对应和数据插值计算这一处理方法是简便、可行的.

2)对三维电磁场有限元计算实例的数据处理及结果显示表明，本文提出的FEM→FDM数据转换计算方法及开发的显示手段是成功和有效的.

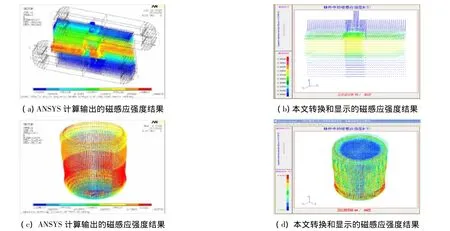
图6 不同电磁计算模型中磁感应强度的ANSYS－FEM模拟结果与本文FEM→FDM数据转换后结果的对比

3)本文FEM→FDM数据转换算法和程序适用于由有限元法计算的任意三维矢/标量场数据向有限差格式转换计算，这一算法及程序与自行开发的3D图形显示软件为实现任意三维电磁凝固传输FEM－FDM耦合数值计算及工艺优化提供了必要的技术手段.

［1］ASAI S.Recent development and prospect of electromagnetic processing［J］.Science and Technology of Advanced Materials，2000，1(4):191－200.

［2］FORT J，KLYMYSHYN N，GARNICH M.Electromagnetic and thermal－flow modeling of a cold－wall crucible induction melter［J］.Metallurgical and Materials Transactions B，2005，36(1):141－152.

［3］DING Hongsheng，CHEN Ruirun，GUO Jingjie，et al.Directional solidification of titanium alloys by electromagnetic confinement in cold crucible［J］.Materials Letters，2005，59(7):741－745.

［4］包燕平，张涛，蒋伟，等.板坯连铸结晶器内钢液流场的三维数学模型［J］.北京科技大学学报，2001，23(2):106－110.

［5］李娇，文光华，祝明妹，等.宽板坯结晶器流场和温度场数值模拟优化分析［J］.重庆大学学报，2009，32(2):173－176.

［6］陈瑞润，丁宏升，郭景杰，等.冷坩埚连续熔铸与定向凝固Ti6Al4V合金的温度场计算［J］.稀有金属材料与工程，2007，36(10):1722－1727.

［7］TANAKA T，YASHIRO N，SHIRAI Y，et al.LPE growth of AlN single crystal using cold crucible under atmospheric nitrogen gas pressure［J］.Physical Status Solid C－Current Topics in Solid State Physics，2007，4(7):2227－2230.

［8］WU Shiping，LIU Dongrong，SU Yanqing，et al.Modeling of microstructure formation of Ti－6Al－4V alloy in a cold crucible under electromagnetic field［J］.Journal of Alloys and Compounds，2008，456(1/2):85－95.

［9］徐艳，康进武，黄天佑.铸造过程温度场/应力场双向耦合的数值模拟［J］.清华大学学报(自然科学版)，2008，48(5):769－772.

［10］李辉，李志强.铸造过程中的应力场数值模拟［J］.中国铸造装备与技术，2007(6):13－15.

［11］李培锋，孙立斌，康进武，等.基于微机的铸件凝固过程应力数值模拟及工程应用［J］.铸造技术，2001 (3):5－8.

［12］BAI Yunfeng，XU Daming，MAO Lihe，et al.FEM/FDM－joint simulation for transport phenomena in directionally solidifying TiAl casting under electromagnetic field［J］.ISIJ International，2004，44(7):1173－1179.

［13］XU Daming，BAI Yunfeng，GUO Jingjie，et al.Numerical simulation of heat，mass and momentum transport behaviors in directionally solidifying alloy castings under electromagnetic fields using an extended direct－simple scheme［J］.Int J Numerical Methods in Fluids，2004，46(7):767－791.

［14］XU Daming，NI Jun.A numerical approach of direct－SIMPLE deduced pressure equations to simulations of transport phenomena during shaped casting［C］//Proceedings of the First International Multi－Symposium on Computer and Computational Sciences.Washington: IEEE Computer Society，2006:815－821.

［15］XU Daming，LI Qingchun.Numerical method for solution of strongly coupled binary alloy solidification problems［J］.Numerical Heat Transfer，Part A，1991，20(2):181－201.

［16］VIVÈS Ch，RICOU R.Fluid flow phenomena in a single phase coreless induction furnace［J］.Metallurgical Transactions B，1985，16(2):227－235.