一款微小型球形机器人的动力学分析

王鹏飞，王 鑫，李满天，孙立宁

(哈尔滨工业大学机器人技术与系统国家重点实验室，哈尔滨150001，wangpengfei1007@163.com)

微小型机器人在侦察与监控等方面特别是对危险环境的探测的应用日益广泛.然而，随着应用范围的扩大，面临的环境也越来越复杂，对机器人的运动性能要求也越高.球型机器人独特的运动原理与外形结构，使它拥有极强的运动灵活性、抗倾覆性和良好的隐蔽性［1］，与普通机器人相比更为适合复杂环境的侦察工作.

球形机器人作为一种非完整性系统，是一个典型的欠驱动机构，其运动学的分析受到了一些学者的关注［2－4］.1996年，芬兰赫尔辛基工业大学自动化实验室的Aarne Halme首次设计了一种球形机器人［5］.2000年 Shourov Bhattacharya和Sunilk Agrawal提出了一种由两个相互垂直的转子构成的驱动系统，利用惯性矩来实现行走与转向，灵活性较好但其驱动力较小［6］.2002年，伊朗学者Amir Homayoun Javadi A.和Puyan Mojabi设计了一种球形机器人，基本实现了系统的全向性运动［7］.机器人的驱动系统是由4个轮辐构成，形成正四面体框架结构.通过调整轮辐上质量块位置实现机器人重心的改变，提供了较大驱动力但控制复杂.1999年，卡耐基梅隆大学的 Brian Chemel等人研制了一款小型球形机器人［8］.机器人直径为14 cm，质量约2 kg.在球形机器人研究方面，国内一些高校也进行了一定研究［9－11］.

本文提出一款采用“重心调节”和“惯性力矩”结合式的球形机器人模型，综合两者的优点，提高了机器人的驱动效率和运动灵活性.并且充分利用空间，将机器人的尺寸缩小仅为直径50 mm，质量为80 g，提高了其隐蔽性.本文对这一球形机器人模型的动力学问题进行了讨论.得到了机器人的直线滚动和原地转动的动力学方程，给出了跳跃运动的起跳条件，并且综合转动和滚动运动，推导出机器人的一种新的复合运动形式，即进动运动.最后进行了虚拟样机仿真，实验验证了上述分析结果.

1 球形机器人物理模型

本文讨论的球形机器人采用“重心调节”和“惯性力矩”结合式的运动方式.其物理模型可以分别在竖直面、水平面上简化为两个相对独立的运动模型.竖直面为滚动运动平面，由一个偏摆电机控制运动;水平面为转动运动平面，由一个旋转电机控制运动.机器人在结构上将滚动运动和旋转运动的惯性配重合二为一，由圆盘形设计的偏心质量块替代.这样的设计大大节省了机器人的内部空间，去除了多余的质量(见图1).同时，通过选取Faulhaber的微小型电机，并且以电机体为机械梁，更提高了空间的利用，并控制机器人内部质量为48 g.

图1 球形机器人结构与实物图

2 球形机器人滚动分析

2.1 滚动动力学方程

机器人的滚动运动依靠偏心质量的偏摆而产生沿竖直平面向前的驱动力.其在竖直面的滚动运动模型可以简化为平面内两个广义坐标θ和x与一个广义力τ组成的力学模型.其运动模型如图2，设球壳质量为M，内部偏心质量为m.

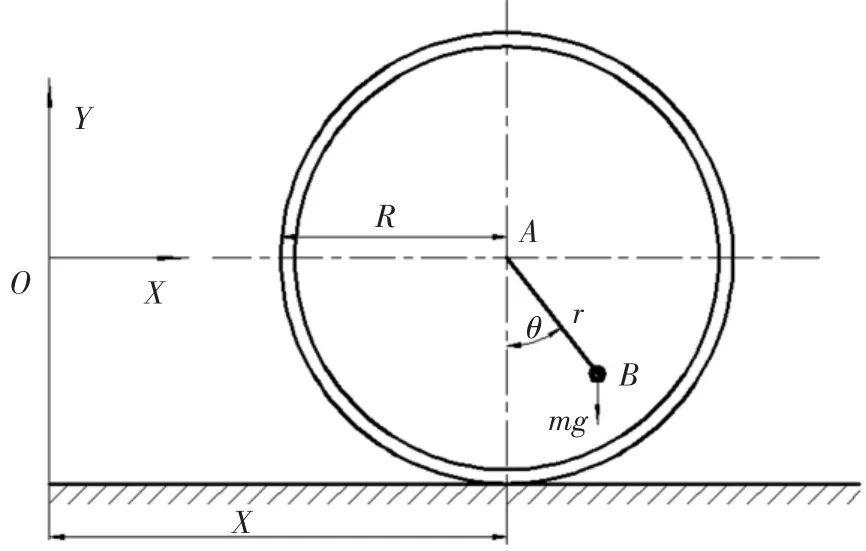
图2 球形机器人滚动模型

此系统为两自由度系统，A点有力矩τ的作用，球壳在地面作纯滚动.但是输入只有电机转矩τ，为典型的欠驱动系统.其动能T和势能V为

可得拉格朗日方程

2.2 滚动特点分析

1)动量守恒

拉格朗日函数L中不显含x，则存在循环积分:

即系统广义动量守恒.从方程式可以看出机器人的滚动运动速度可以通过控制其摆角值实现.即摆角速度˙θ=0，控制摆角增大时(θ⇒90°，cos θ⇒0)，则滚动速度 ˙x将随之提高.

2)跳跃分析

利用运动方程，设地面支持力为N，当N≤0时，即为球形机器人的起跳条件.可得竖直方向力平衡方程:

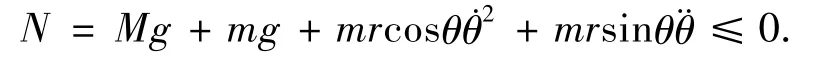
设机器人由静止起跳忽略滚动项，带入方程(1)整理，可得

方程第一个括号内，恒为正.因此当θ角在第三象限时，使得方程(2)的后一括号内为负，从而可能使方程满足起跳条件.即当θ获得较大速度时，或电机输出较大转矩时，机器人可能产生跳跃运动.

3 球形机器人转动分析

对于原地转动运动，转轴与竖直轴重合，使得自旋运动与滚动运动相对独立，转动模型如图3，其中内部旋转质量在旋转电机的带动下转动，转速 ˙φ，转动惯量JB;球壳转速 ˙Ω，转动惯量JA;地面给球体的阻力矩为Mμ.

图3 球形机器人旋转运动模型

对于z轴，力矩守恒方程为

对等式积分可得速度关系

分析所得方程:

4 球形机器人进动分析

4.1 进动趋势的导出

将机器人内部系统从球体系统中独立出来，则去除了球壳对内部系统的影响，并且不受地面等的阻力影响.机器人内部系统具有两个可控的输入，即滚动偏角θ和转动速度其中滚动偏角θ由偏摆电机控制，保持恒定值.选择与配重圆盘刚体固结的主轴坐标系为动坐标系，选择球体竖直转动坐标系为系统定坐标系，该坐标系为内部系统的虚拟坐标系，仅为说明本节问题所建立.其运动模型如图4，配重圆盘转速为，系统虚拟旋转主轴z0，系统绕虚拟主轴转速由于梁架相对配重圆盘质量小得多，所以忽略梁架质量.

图4 球形机器人进动运动模型

动坐标系Oxyz的转动角速度为

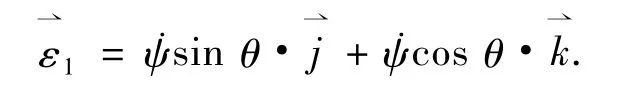
外力矩

代入欧拉方程可得

在运动过程中，Mx=－mgrsin θ+τ，由直线运动偏摆电机输入力矩和滚动运动偏角决定，在平稳运动时偏摆力矩平衡，水平轴所受力矩Mx=0.

则由方程(3)第一式得

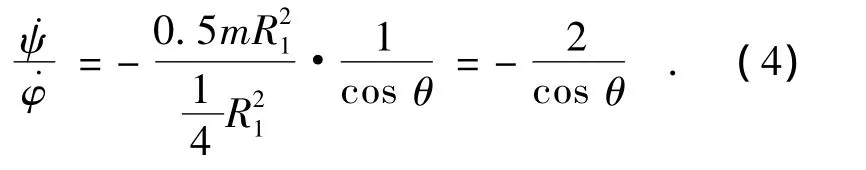
当有偏角θ时，圆盘将有由转动产生的

的进动运动趋向.

4.2 球体的进动转动

将上述的进动系统与机器人球体相结合，即引入球壳质量和地面摩擦力的影响.则当机器人正常滚动时存在偏角θ，内部系统将产生绕z0轴的的运动趋向.设内部系统绕z0轴的转动惯量为Jp，由动量定理可得

可见机器人在滚动运动时配合转动，可以实现在前进过程中的以球体瞬时竖直轴为转轴的转动和滚动的复合运动.

4.3 机器人运动整合

将式(1)、(5)联立，即为该球形机器人在动坐标系(x－O－y)的通用动力学模型(如图5).通过控制摆角θ，可以控制机器人的滚动速度;通过控制转动速度 ˙φ，使其与滚动运动相耦合，产生进动运动，实现机器人在运动过程中的转向.

图5 机器人整合运动坐标示意图

通过变换，可以获得在定坐标系(m－O－n)中的通用动力学方程:

这种运动形式实现了机器人沿任意曲线的运动.这样的运动增大了机器人对复杂环境的适应能力.但是要指出的是，进动运动是一种耦合运动，即在该运动情况下不能实现转速和滚动速度的分别控制.

5 虚拟样机仿真与实验

为验证上述理论模型的正确性，根据机器人实体参数设定如下:R=25 mm，r=20 mm，M=34 g，m=48g，JA=13 500 gm2，JB= 3 800 gm2，μ=0.3.在虚拟样机仿真分析软件ADAMS中建立了三维模型，其中具体参数含义参考表1.虚拟样机仿真模型及运动曲线如图6.

表1 球形机器人参数

图6(a)为在ADAMS中建立的虚拟样机模型.在仿真分析中，梁架与球壳连接处沿x轴添加回转副，偏心质量与梁架连接处沿y轴添加回转副，球壳与地面添加接触力和摩擦.在两个回转副加入电机转速信息进行模拟仿真，获得机器人的运动特性曲线.

在偏摆电机输入恒定转速9 000(°)/s，进行跳跃运动动力学仿真，可得球形机器人跳跃高度曲线(如图6(b)).由图可得跳跃高度可达4.5 cm，证明了在电机输入功率达到一定值时，机器人可以实现跳跃运动.但是在实体样机上实现跳跃运动还需要一定的改进.

在旋转电机输入恒定转速90(°)/s、有摩擦力作用，进行转动运动动力学仿真可得球形机器人转动运动角速度曲线(如图6(c)).按上述模型计算，角速度由－25.3(°)/s逐渐减小为零，与仿真结果相对照，吻合较好.在实体样机上，通过对旋转电机输入一系列方波，使机器人实现了非匀速的连续转动.

在偏摆电机输入恒定转速30(°)/s，1s后旋转电机再输入恒定转速90(°)/s，进行运动仿真得到球形机器人在水平面(x－z平面)的位移曲线(如图6(d)).验证了球形机器人在两轴电机同时作用时产生进动运动，实现了机器人沿曲线运动.在实体样机中应用上节的理论分析，实现了转动和滚动的整合运动.

6 结论

1)本文对微小型球形机器人的滚动运动和转动运动进行了动力学分析，并讨论了机器人跳跃运动的起跳条件.

2)通过对其滚动运动和转动运动的动力学分析的综合，得出机器人进动运动形式的动力学方程，进而建立出整合运动通用的动力学模型.扩展了机器人的运动形式，提高了其对环境的适应性.

3)对机器人各运动形式的特点进行了分析，利用仿真软件进行了虚拟样机仿真，并通过实验验证了分析结果.

［1］邓宗全，岳明.球形机器人的发展概况综述［J］.机器人技术与应用，2006(3):27－30.

［2］SUN Hanxu，XIAO Aiping，JIA Qingxuan.Omni directional kinematics analysis on bi-driver spherical robot［J］.Journal of Beijing University of Aeronautics and Astronautics，2005，31(7):736－739.

［3］王亮请，孙汉旭，贾庆轩.球形机器人的跳跃运动分析［J］.机械设计，2006，23(3):28－30.

［4］岳明，邓宗全.基于欧拉角描述下的球形机器人动力学建模与分析［J］.哈尔滨工业大学学报，2008，40 (1):43－46.

［5］HALME A，SCHONBERG T，WANG Y.Motion control of a spherical mobile robot［C］//4thInternational Workshop on Advanced Motion Control.［S.l.］:Mie University，1996:259－264.

［6］SHOUROV B，SUNIL K A.Spherical Rolling Robot:A Design and Motion Planning Studies［J］.IEEE Trans on Robotics and Automation，2000，16(6):835－836.

［7］AMIR H J A，PUYAN M.Introducing Glory:A Novel Strategy for an Omni directional Spherical Rolling Robot［J］.Trans ASME，2002，126:678－683.

［8］CHEMEL B，MUTSCHLER E，SCHEMPF H.Cyclops: Miniature Robotic Reconnaissance System［C］//Proceedings of the 1999 IEEE International Conference on Robotics＆Automation.Detroit:IEEE，1999:2298－2302.

［9］ZHAN Qiang，JIA Chuan，MA Xiaohui.Mechanism design and motion analysis of a spherical mobile robot［J］.Chinese Journal of Mechanical Engineering，2005，18(4):542－545.

［10］ZHAN Qiang，JIA Chuan，MA Xiaohui.Analysis of moving capability of a spherical mobile robot［J］.Journal of Beijing University of Aeronautics and Astronautics，2005，31(7):744－747.

［11］邓宗全，岳明，禹鑫，等.球形运动器动力学分析及控制系统设计［J］.机器人，2006，28(6):565－570.