喷管内雾状气液两相流场计算分析

付英杰，魏英杰，张嘉钟，董 磊

(哈尔滨工业大学航天学院，哈尔滨150001，fuyj2271@sina.com)

气液两相流广泛存在于现代工业设备当中，如锅炉、核反应堆蒸汽发生器等汽化装置，石油、天然气的输送管道，各种蒸发器、冷凝器、反应器等化工设备，以及气液混合器、热交换器等.雾状流作为气液两相流的一种重要流型，常用于灭火器，各种发动机燃烧室以及水下推进装置中等.

国内外对雾状气液两相流的研究主要集中在液体碎裂过程及实验测量技术等方面［1－4］，关于两相流动的详细分析相对较少.Eddington［5］基于双流体模型对超声速雾状流进行了理论分析，研究了两相流中正激波及斜激波特性;并进行了实验研究，分析结果与实验对比有很好的一致性.魏文韫［6］采用理论分析和实验的方法，研究了由拉伐尔喷管产生的高速气－雾两相流发生过程中动量传递的弛豫现象，为这一特殊的反应体系提供了流体动力学基础.郭烈锦［7］总结了前人关于气液两相流的研究工作，并进行了系统研究分析.

Muench和Keith［8］提出一种向水下喷气推进装置中通过雾化喷嘴注入液相水，与气体混合形成雾状流并由喷管高速喷出，借以增加发动机推力及效率的方法，并把该推进装置称为喷雾推进器.该推进器主要包括空气压缩单元、水注入单元和两相喷管3个部分，研究表明推进效率可以达到50%.该喷雾推进器以雾状气、水混合物作为工作介质，因此喷管内雾状气液两相流场计算，对于该推进器的性能分析有重要影响.本文基于双流体模型，针对喷管内雾状气液两相流，考虑了两相间的动量、热量传递，分别进行了亚声速和超声速两相流动的计算分析;在此基础上，进一步研究了液滴尺寸及初始含气率对雾状两相流场分布的影响，旨在为喷雾推进器性能分析等研究工作打下基础.

1 计算模型

针对喷管内雾状气液两相流，参考Muench［9］所采用的双流体模型，进行流场计算;模型所作的假设如下:1)流场是准一维稳态的，即各相速度、压力等参数在同一喷管截面上为单一值，且不随时间变化，液滴均匀分布;2)气相为理想气体，液相为不可压缩流体;3)流场中液滴始终保持球形，且不发生分裂或合并，直径不变;4)不考虑喷管壁面与流体间的摩擦应力、湍流及边界层效应对流场影响.

气相与液相连续性方程如下:

式中:下标L，G分别表示与液相、气相对应的变量;α为截面含气率，即空隙率;ρ，u分别为对应相的密度和速度;A为喷管任意点处截面面积;˙mL，˙mG分别为液相、气相的质量流率.

混合相动量方程，

式中，p为流场压力.

液体微团(液滴)动量方程为

式中，Re为基于相间滑移速度的液滴雷诺数，且

式中:右侧项分别为作用于液滴的压力梯度力及两相间粘性阻力;D为液滴直径，CD为液滴微团阻力系数，可通过下式求得［9］:

其中:μG为气体动力粘度.

忽略喷管壁面与两相流间的热量传递，则两相流总能量方程可表示为

式中:T为对应相温度，cp为气相定压比热容，c为液相比热.

两相间热量传递方程为

式中:左侧项为液滴热能增加值;右侧项为通过对流作用液滴吸收的热量;h为对流换热系数，根据相似准则努谢尔数(Nusselt number)计算得到［9］.

气相为理想气体，满足状态方程

式中:RG为气体常数.

方程(1)～(7)组成了描述喷管内雾状气液两相流的完整模型方程组，通过求解该常微分方程组，可以得到两相流场参数在喷管内的分布情况.

与单相可压缩流不同，在两相流中，尤其是两相速度差异较大的雾状流，声速和临界流速并不统一，两者关系比较复杂.两相临界流的问题，截止到目前仍在继续研究中，且远未达到取得确切结论的程度［10］，故这里只给出声速及临界流速的经验表达式［7］，在进行喷管内临界两相流场计算时，仅对其进行定性分析.气液两相流中声速方程式如下:式中:cG为单相气体中声速值.

当气液两相间滑移速度较大时，临界流速与声速差异较大，可表示为

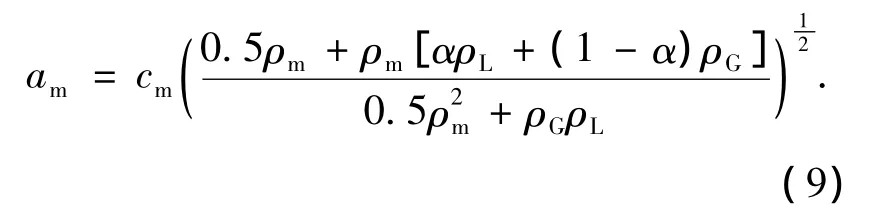
式中:两相混合密度ρm=αρG+(1－α)ρL.

两相混合物速度为

此外，整首诗歌采用象征手法对相关内容进行隐喻，从而形成多层次的表达形式和复杂的情感内容。多个意象如“橡树”、“木棉”、“凌霄花”等，意象新奇而具有陌生化效果，在文本语境中朦胧而极富意味，在它们的共同作用下，《致橡树》不仅完成了朦胧诗美的表达，更完成了舒婷对女性独立意识的强调和理想两性关系的建构。

马赫数为

两相滑动比为

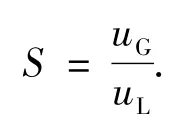
2 数值方法

模型方程组中包含7个常微分方程，但含有ρG，uG，uL，α，p，TG，TL，A等8个未知量;在进行流场计算时，需要给定某一个函数分布，进而计算其它变量.亚声速流场计算时，采用半收缩角为β的锥形喷管，则喷管截面面积A随轴向坐标x变化关系如下:

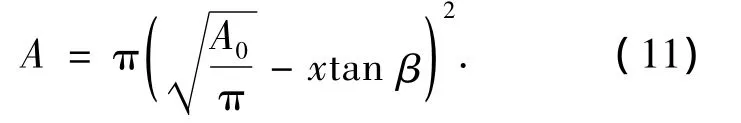
式中:A0为喷管入口截面面积.

此时，模型方程组可整理为

式中:

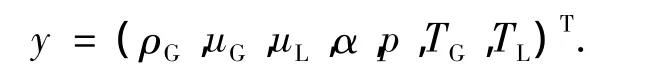
该方程组为一阶常微分形式，通过变步长的Runge－Kutta法求解方程组，当流场压力降为环境压力时，停止计算，可得到亚声速流场参数分布.

给定喷管轮廓即喷管截面面积的方法，只适用于亚声速流场计算.若给定缩放喷管轮廓进行超声速流场计算，可能在喷管喉部以前发生阻塞，得不到稳定的稳态解;或者在喷管喉部仍未达到临界条件，故在扩张段流体速度会减小，达不到超声速流场计算分析的目的.本文在进行喷管内超声速两相流计算时，给定流场压力p随喷管轴向坐标x的变化关系，即

3 计算结果与讨论

在文献［9］中Muench和Ford将该模型计算结果与实验进行了对比，两者吻合较好，验证了该计算模型及计算方法的准确性，故本文不再重复验证，重点应用该模型对喷管内雾状气液两相流场进行计算分析.

3.1 亚声速流场分析

采用半收缩角β=10°的锥形收缩喷管，则截面面积沿轴向分布如方程(11)，喷管入口截面面积A0=7.85×10－3m2.入口处液相速度uL0= 20 m/s，气相速度 uG0=2uL0，液相温度 TL0= 293 K，气相温度TG0=350 K，含气率α0=0.9，压力p0=2×105Pa，环境压力p∞=105Pa，液滴直径D=10－4m，进行喷管内亚声速两相流场计算分析.如图1～2给出了该条件下，雾状气液两相流场参数沿喷管轴向的分布情况，其中L为流场压力降为环境压力时得到的喷管长度;下标e表示喷管出口处流场变量.

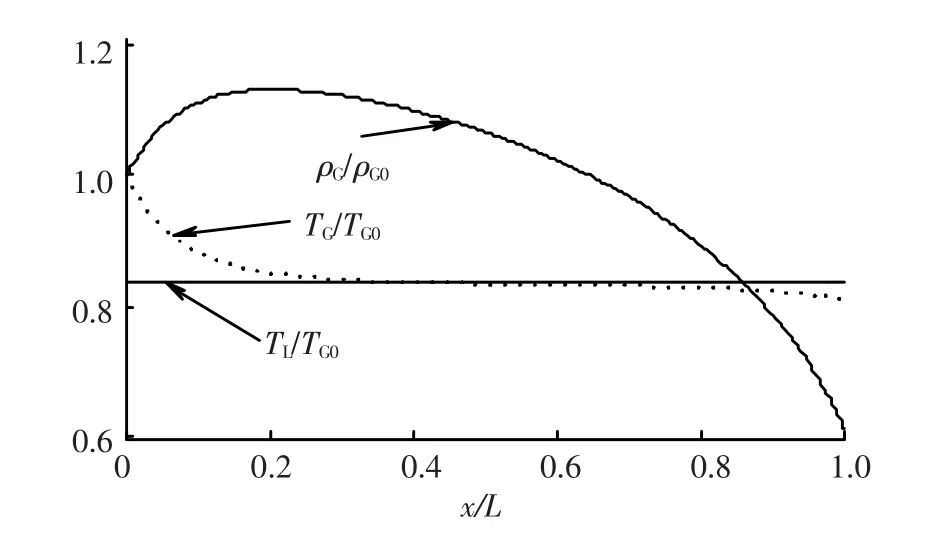
图1 ρG，TG及TL沿喷管轴向分布曲线

图2 p，uG及uL沿喷管轴向分布曲线

由图1可知，由于对流传热及气体膨胀加速作用，气相温度逐渐降低，与液相温度趋于一致.液相比热容约为气相的4倍，质量流率也远大于气相(此条件下两相质量流率比 ˙mL/˙mG约为28)，故液相温度变化很小.由于在喷管入口附近温度下降较快，致使气相密度增大，因而气相速度在喷管入口附近略有减小，如图2所示.随着压力的降低，气、液两相速度同时增大，但气相速度增长较快，在喷管出口附近两相速度差异达到最大.

喷管入口两相温度TG0=TL0=293 K，改变液滴直径D，其它条件同上，进行雾状两相流场计算，分析液滴直径对流场分布的影响，如图3～5所示.

可见，在各液滴尺寸条件下，压力均沿喷管轴向逐渐减小，且压力梯度(－dp/dx)随液滴直径的减小而增大，即压力下降速度逐渐增大，因而由入口压力膨胀到环境压力所需要的喷管长度，随液滴直径的减小而减小.喷管出口处，液相速度随液滴直径的减小而增大，气相速度随其减小而减小;各条件下，喷管出、入口两相动量变化率依次为:412.2 N，466.4 N，531.5 N，601.1 N，可见动量变化随着液滴直径的减小而逐渐增大，因此减小液滴尺寸有利于增大雾状流通过喷管喷射所产生的推力值.

图3 液滴直径D对流场压力分布影响

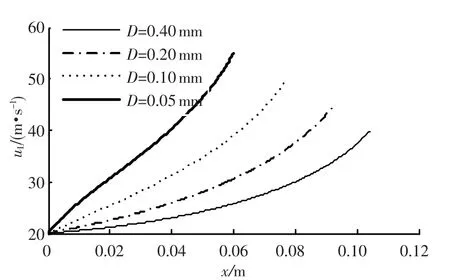
图4 液滴直径D对液相速度分布影响

图5 液滴直径D对气相速度分布影响

其它条件保持不变，改变初始含气率值，进行两相流场计算分析，研究初始含气率对流场分布的影响.如图6～8，分别给出了各条件下流场压力，液相及气相速度喷管轴向的分布情况.随着初始含气率的增大，压力梯度(－dp/dx)逐渐减小，膨胀到环境压力所需要喷管长度增大.初始含气率较高时液相速度增长缓慢，气相速度随初始含气率变化趋势与液相类似.在喷管出口处，液相及气相出口速度均随着初始含气率的增大而增大.由于初始含气率增大时，减小了液相质量流率，致使初始含气率分别为0.85，0.90，0.95时，通过喷管时两相动量变化率依次为: 591.9 N，531.5 N，431.6 N，即在一定条件下，随着初始含气率增大，通过喷管时两相动量变化逐渐减小.

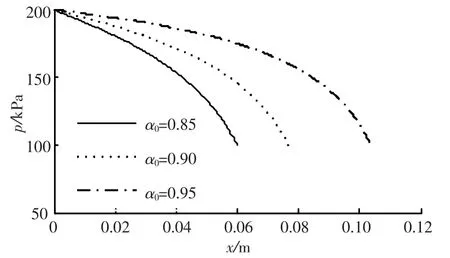
图6 初始含气率α0对流场压力分布影响

图7 初始含气率α0对液相速度分布影响

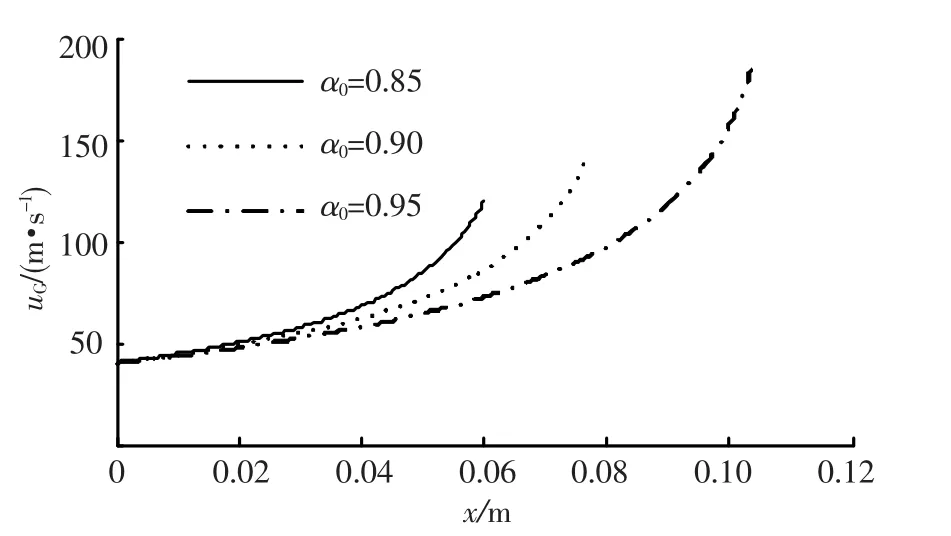
图8 初始含气率α0对气相速度分布影响

3.2 超声速流场分析

提高两相混合流在喷管出口处速度值，可以增大雾状流喷射所产生的推力.然而气液两相流中声速远小于单相气体或液体物质中声速值，故水下发动机喷管内两相流动多为超声速，本节重点对喷管内超声速雾状气液两相流进行计算分析.

假定流场压力沿喷管轴向分布如方程(12)，取初始压力p0=4×105Pa，环境压力p∞= 105Pa.气相温度TG0=350 K，液相温度TL0= 293 K，其它条件与亚声速流动分析时相同，使两相流在喷管内膨胀到环境压力，对流场进行分析.各流场参数分布情况如图9～10所示，其中气相出口速度uGe=214.6 m/s.

由喷管截面面积分布可知，喷管为缩放型，喉部位置x/L=0.737，而两相流在缩放喷管内一直处于加速状态，可认为两相流动为超声速.两相温度及气相密度沿喷管轴向分布均与亚声速相似.气体在喷管内膨胀过程中，把气相内能转化为气相和液相动能，同时通过对流传热向液相传递热量，气相温度降低，液相温度略有升高;当气相温度低于液相时，再次通过对流传热，从液相吸收热量，致使液相温度随之降低;可以认为，两相混合物在喷管内流动时，把气相及液相内能转化为两相动能.

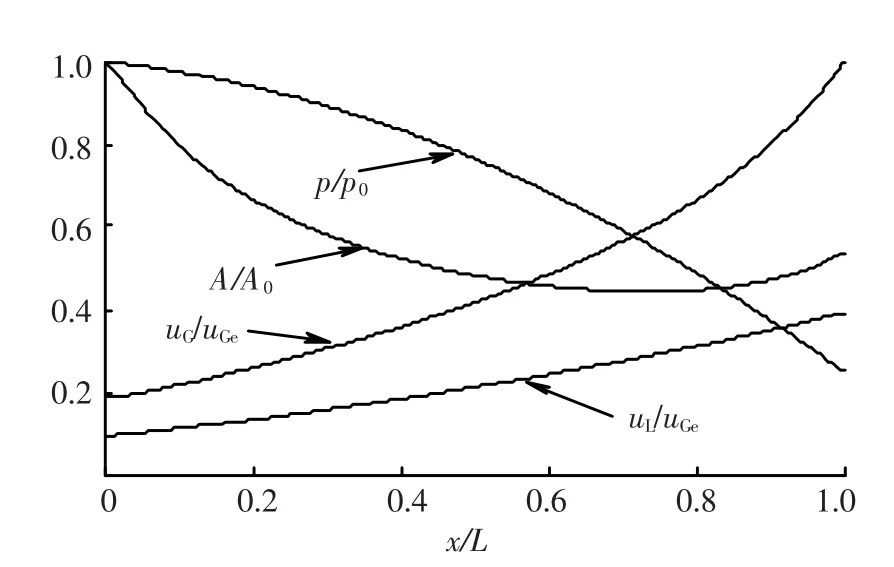
图9 p，A，uL及uG沿喷管轴向分布曲线

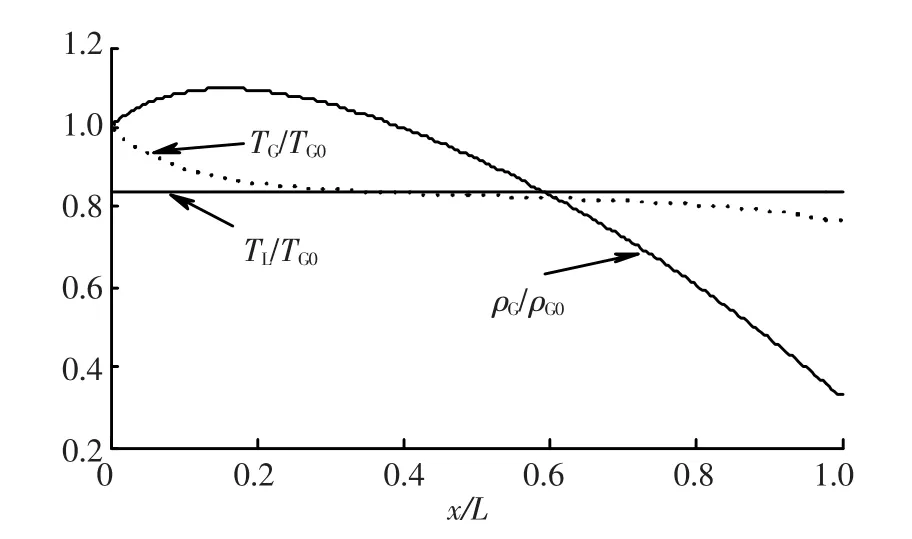
图10 ρG，TG及TL沿喷管轴向分布曲线

通过方程(8)～(10)计算得到的气液两相流中声速cm，临界流速am及混合相速度Vm沿喷管轴向的分布情况，如图11所示.可见声速及临界流速均沿喷管逐渐减小，并且临界流速略大于声速值;但在喷管喉部位置，混合相速度与喉部临界速度或声速并不相等，即马赫数M不等于1，而是在喉部后方某一位置混合相速度与临界流速达到一致，主要由于声速表达式(8)是基于冻结模型求得的，得出的结果偏高.当两相流间存在较大的滑移速度时，声速及临界流速的计算有待于进一步研究.

流场压力分布等其它条件不变，改变液滴直径D进行喷管内超声速两相流场计算，图12～14分别给出了两相速度及喷管截面面积沿轴向的分布情况.

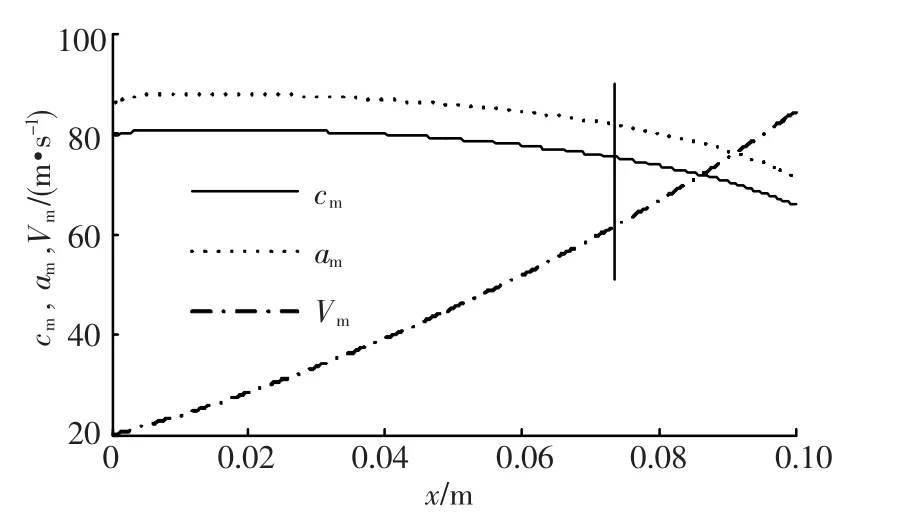
图11 声速、临界流速及混合相速度沿喷管分布

图12 液滴直径D对液相速度分布影响

图13 液滴直径D对气相速度分布影响

图14 液滴直径D对喷管截面面积分布影响

可见，当液滴直径较小时，液相速度增长较为迅速而气相速度增长缓慢，则在喷管出口处，液相速度随液滴直径减小而增大，气相速度随其减小而减小.由图14可知，随着液滴尺寸的减小，喷管喉部面积逐渐增大，位置变化不大(D取0.4 mm， 0.2 mm，0.1mm 时，喉部分别位于 x = 0.074 8 m，0.074 5 m，0.073 8 m处);在喉部位置气相速度随液滴直径减小而减小，液相速度随其减小而增大;两相滑动比S分别为3.19，2.61和2.10，马赫数M为0.855，0.868和0.874;可见随着两相间滑动比的减小，喉部马赫数逐渐接近于1.

图15～17给出了不同初始含气率α0条件下，气相速度、液相速度及喷管截面面积沿喷管轴向的分布情况.

图15 初始含气率α0对气相速度分布影响

图16 初始含气率α0对液相速度分布影响

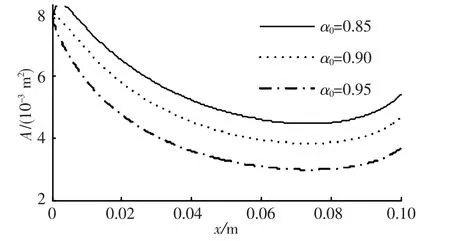
图17 初始含气率α0对喷管截面面积分布影响

由图可知，两相速度均随着初始含气率的增大而增大;喷管喉部面积随着含气率的增大而减小，而喉部位置几乎没有变化(分别位于x= 0.073 8 m，0.073 8 m，0.073 9 m处).初始含气率对通过喷管时两相动量变化率 Δ(˙mLuL+ ˙mGuG)的影响与亚声速流动情况下相同.

4 结论

1)液相速度增长缓慢，两相速度差异逐渐增大，在喷管出口处速度差异为最大;

2)亚声速及超声速流动中，液相出口速度均随液滴尺寸减小而增大，气相出口速度随其减小而减小;液相、气相出口速度均随着初始含气率的增大而增大;

3)超声速流动中，喉部混合相速度、声速及临界流速均不相等，且滑动比越小，混合相速度越接近声速;喉部面积随初始含气率、液滴直径的增大而减小，位置变化不大.

［1］CAO J M.Derivation on the linear stability theory of plane liquid sheets spray in two compressible gas streams［J］.Combustion Science and Technology，1999，(4):349－355.

［2］JAZAYERI S A，LI X.Nonlinear instability of plane liquid sheets［J］.Journal of Fluid Mechanics，2000，406(3):281－308.

［3］CAO J M.On the theoretical prediction of fuel droplet size distribution in nonreactive diesel sprays［J］.Journal of Fluids Engineering，ASME Trans.，2002，124 (1):182－185.

［4］WILD P N，SWITHENBANK J.Beam stop and vignetting effects in particle size measurements by laser diffraction［J］.Applied Optics，1986，25(19):3520－3526.

［5］EDDINGTON R B.Investigation of supersonic phenomena in a two－phase(liquid－gas)tunnel［J］.AIAA Journal，1970，8(1):65－74.

［6］魏文韫.高速气雾两相流弛豫过程相间动量传递研究［D］.成都:四川大学，2002.

［7］郭烈锦.两相与多相流动力学［M］.西安:西安交通大学出版社，2002.

［8］MUENCH R K，KEITH T G Jr.A preliminary parametric study of a water-augmented air-jet for high-speed ship propulsion［R/OL］.1967，MEL-358/66.http:// oai.dtic.mil/oai/oai?＆verb=getRecord＆metadata Prefix=html＆identifier=AD0647153.

［9］MUENCH R K，FORD A E.A water－augmented air jet for the propulsion of high－speed marine vehicles［J］.Journal of Hydronautics，1970，4(4):130－135.

［10］鲁钟琪.两相流与沸腾传热［M］.北京:清华大学出版社，2002.