假设法在数学中的应用例举
2010-03-23蔡青
■蔡青
假设法在数学中的应用例举
■蔡青
在小学数学中,有些类型的题目呈现出一个共同的特点:题目中要求两个未知量,这两个量有各自的数量标准,通过两个不同的数量关系相关联,有点像初中的二元一次方程解决的问题,但又不完全是。而作为小学生,解决此类问题往往用算术方法,着实有一定难度。然而,如果我们能够辩证地看待这些问题,使用假设法巧妙地分析其数量关系,往往能使问题得到很好的解决。这种假设法解题的核心思想是:将两种标准不同的数量按其中一种数量的标准假设,通过分析在这种假设之下数量关系的变化,从而找到数量之间的对应关系,求出各个数量。
例1.鹅羊三十六,共计一百足,鹅羊各多少只?
分析:这是一道典型的鸡兔同笼问题,一只鹅2条腿,一只羊4条腿,若将36只全部按鹅的标准假设,即全部按2条腿算,则由2×36=72条腿,比实际少100-72=28条腿,而这正是每只羊少算2条腿的总和,因此羊的只数为:28÷(4-2)=14(只),鹅的只数为:36-14=22(只)。解答如下:
羊的只数:(100-2×36)÷(4-2)=14(只)
鹅的只数:(4×36-100)÷(4-2) =22(只)
例2.两个杯中分别装有浓度为40%与10%的食盐水,倒在一起后混合食盐水的浓度为30%;若再加入300克20%的食盐水,则浓度变为25%,那么原有40%的食盐水多少克?
分析:此题解法为先求出浓度为30%的食盐水重量,再求出浓度为40%的食盐水重量。
解法:(1)浓度为30%的食盐水重量:
300×(30%-20%)÷(30%-25%)-300=300(克)
(2)浓度为40%的食盐水重量:
300×(30%-10%)÷(40%-10%)=200(克)
例3.100个和尚吃100个包子,大和尚1人吃3个,小和尚3人吃1个。问:大和尚、小和尚各多少人?
分析:此题将小和尚吃的包子数按大和尚的标准假设,则包子总数必然超过100个,超出的个数恰恰是所有小和尚多计算的包子数的总和,即可求出小和尚人数,同理,反之可求出大和尚人数。
解法(1):小和尚人数:(100× 3-100)÷(3-)=75(人)
大和尚人数:100-75=25(人)
小和尚人数:100-25=75(人)
例4.一根长绳的长度是一根短绳的3倍,各剪去20米后,长绳剩下的长度是短绳剩下的长度的4倍。长绳原来有多长?
分析:利用方程解此题是比较简单的,但有的学生不一定会解方程,而算术解法也不好解,因为此题中长绳与短绳这两个量都变了,他们的和也变了,只有它们的差没变,但却难以建立标准量与对应量之间的对应关系,但使用假设法却会使此题变得很容易。我们不妨假设短绳剪去20米后的长度为a米,则短绳长度为(a+20)米,假如原来长绳的长度是长绳长度的4倍,那么长绳的长度就有4(a+20)=4a+4×20,长绳原来的长度是4a+20,如果是4倍,还差3×20,而3×20恰恰是短绳的1倍,于是,原来短绳长度为60米,原来长绳长度为60×3=180(米)。
线段图分析:
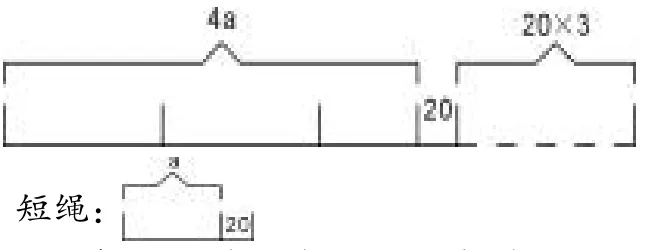
解:20×(4-1)×3=180(米)
答:原来长绳长180米。
总之,假设法在小学数学中有着广泛的应用,绝不仅仅限于以上几种题。有人说过这样一句话——“思想有多远,我们就能走多远。”在数学王国这片天地里,数学问题的解决,往往是由人的思维方式来决定的,不同的思维方式决定了不同的解题思路。假设法恰恰是打破常规思维方式的一种有效的解题思维,在不经意间往往会收到意想不到的效果。
(作者单位:武汉市新洲区汪集街冯铺小学)
责任编辑 廖林
